Нормальный закон распределения (закон Гаусса)
Этот закон является одним из наиболее распространенных законов распределения погрешностей, что объясняется центральной предельной теоремой теории вероятностей. Центральная предельная теорема ТВ - распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа неравномерно действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Закон Гаусса имеет следующее выражения:
MX - математическое ожидание, оно является центром группирования результатов наблюдения. G - среднеквадратичное отклонение характеризует величину рассеивания результатов наблюдений, т.е. точность измерения. Центральный момент первого порядка.
Сколько бы не измеряли все моменты располагаются около МХ при n®¥. Центральный момент второго порядка.
Дисперсия – математическое ожидание квадрата отклонения случайной величины от квадрата ее математического ожидания. В практике неизвестно МХ, поэтому:
Так как среднее арифметическое
Видно, что эмпирическое среднее квадратическое отклонение среднего арифметического значения в Зная MX и G, можно с определенной вероятностью определить диапазон рассеивания результатов наблюдений D.
где z - коэффициент равный значению функции Лапласа.
68% - доверительная вероятность В этом интервале лежат 68% всех размеров, среднеквадратическое отклонение является 68% или доверительным интервалом.
95% - в промышленности 99.73% - в научных исследованиях Доверительный интервал, интервал в котором мы ожидаем размер. Доверительная вероятность - вероятность того, что размеры деталей или результаты измерения окажется внутри доверительного интервала. За оценку случайной погрешности результата измерений принимают доверительный интервал среднего арифметического. Случайные погрешности, > 3G, считаются грубыми и исключаются из результата измерения. При малом n используют коэффициент Стьюдента, где При n®¥ распределение Стьюдента переходит в нормальное распределение, чем больше n, тем меньше коэф. Стьюдента, интервал с заданной вероятностью уменьшается
Систематическая погрешность.
Суммирование погрешностей.
1. Систематические погрешности суммируются алгебраически:
2. Случайные погрешности суммируются квадратически.
При расчёте предельной погрешности измерения определяют числовое значение погрешности измерения от всех составляющих и производят суммирование:
где знаки "+" или "-" ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю. Если в случайной погрешности известно среднее квадратическое отклонение, то
где К - показатель, указывающий доверительные границы для предельной случайной погрешности измерения (при К=1 р=0,65; при К=2 р=0,945; при К=3 р=0,9973). Если результаты измерений зависят от большого числа разнообразных факторов, то y = F(x1, x2, …..xn), где xi - переменные функциональные параметры. Каждый параметр может иметь отклонение Dxi (погрешность) от предписанного значения xi. Поскольку погрешность Dxi мала по сравнению с величиной xi, суммарная погрешность Dy функции y можно вычислять по формуле
где ¶y/¶xi - передаточное отношение (коэффициент влияния) параметра xi. Формула (3.1) справедлива лишь для систематических погрешностей Dxi. Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть
Суммарная погрешность при наличии только случайных составляющих dxi погрешностей
где m - число попарно корреляционно связанных параметров; ki и kj - коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального; rij - коэффициент корреляции, существующий при наличии корреляционной связи между параметрами xi и xj. При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности: Dyсум = Dy ± k×sy , где k - масштабный коэффициент интервала распределения, зависящий от закона распределения и принятой доверительной вероятности. Так, при доверительной вероятности Р = 0,95 для закона нормального распределения k = 2, а для закона Максвелла k = 3,6. Пример. В результате измерений и последующего вычисления по формуле (3.1) получена суммарная систематическая погрешность результата измерения Dy = -0,7 мкм, среднее квадратическое этого результата измерения, вычисленное по формуле (3.2) sy = 0,4 мкм. При доверительной вероятности Р =0,95 предел допускаемой погрешности dизм = +1 мкм. Тогда верхняя и нижняя доверительные границы погрешности Dyсум в = -0,7 + 2×0,4 = +0,1 мкм; Dyсум н = -0,7 - 2×0,4 = -1,5 мкм. Так как Dyсум н > dизм , выбранный метод и средство измерения не удовлетворяют требованиям точности. Следовательно, необходимо скомпенсировать систематическую составляющую погрешности, например, путём изготовления образца для настройки измерительного средства. Размер образца должен быть больше его начального размера на 0,7 мкм; тогда будет справедливо неравенство 0,8 < 1 мкм и проведённые измерения будут удовлетворять требованиям по точности.
|

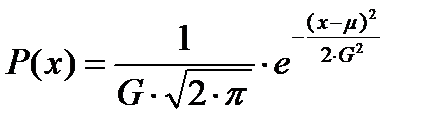
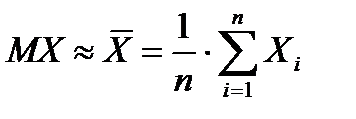
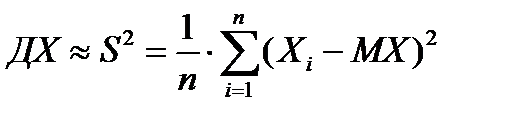 ДХ – дисперсия
ДХ – дисперсия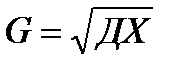 - характеризует величину рассеивания результатов наблюдения.
- характеризует величину рассеивания результатов наблюдения.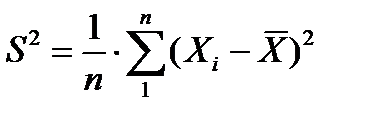 - смещенная характеристика поскольку ее математическое ожидание
- смещенная характеристика поскольку ее математическое ожидание 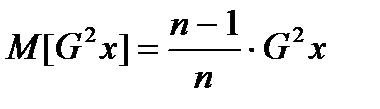
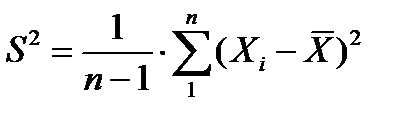 - несмещенная характеристика дисперсии.
- несмещенная характеристика дисперсии.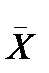 вычисляется по результатам отдельных наблюдений, то
вычисляется по результатам отдельных наблюдений, то 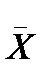 является тоже случайной величиной и характеризуется своим эмпирическим средне квадратическим отклонением
является тоже случайной величиной и характеризуется своим эмпирическим средне квадратическим отклонением 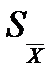

 раз меньше эмпирического среднего квадратического отклонения, (т.е. точность среднего арифметического значения в
раз меньше эмпирического среднего квадратического отклонения, (т.е. точность среднего арифметического значения в 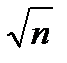 раз выше точности единичного измерения). Поэтому на практике за результат измерения принимают
раз выше точности единичного измерения). Поэтому на практике за результат измерения принимают 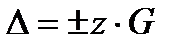
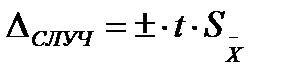
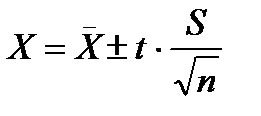 , P=, n=
, P=, n=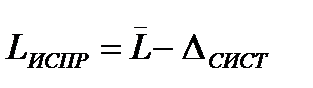
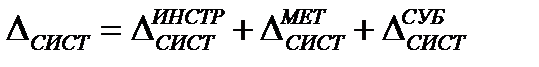
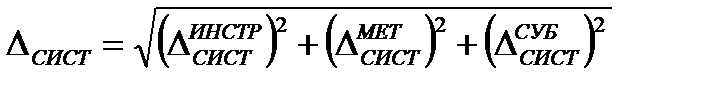
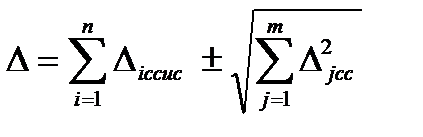 ,
,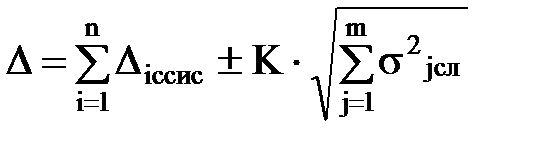 ,
,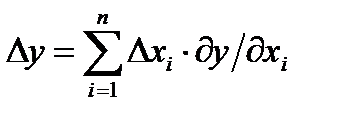
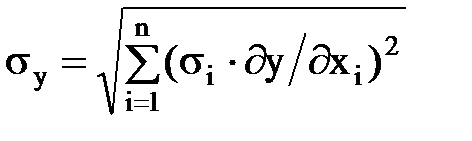 . (3.2)
. (3.2)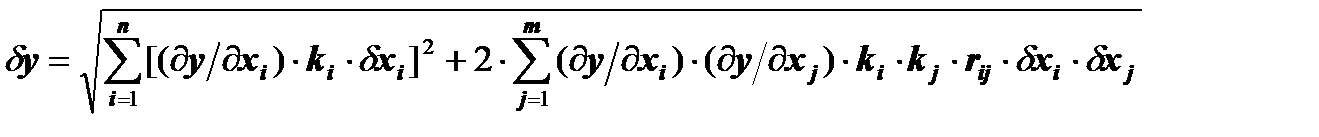 ,
, 



