Обработка результатов многократных измерений
Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах — это результат xп отдельного наблюдения, входящего в ряд из n наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного. При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое
Затем вычисляют оценку СКО результата наблюдения как
Находят отклонение vп предполагаемого промаха xп от vп = | xп - По числу всех наблюдений n (включая xп) и принятому для измерения значению Р (обычно 0,95) по теории вероятностей находят z(P,n) — нормированное выборочное отклонение нормального распределения. Если v п < z×S(x), то наблюдение xп не является промахом; если v п ³ z×S(x), то xп — промах, подлежащий исключению. После исключения xп повторяют процедуру определения За результат измерения принимают среднее арифметическое Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле
В предположении принадлежности результатов наблюдений хi к нормальному распределению находят доверительные границы случайной погрешности результата измерения при доверительной вероятности Р по формуле Î (P) = t(P,n) × S( где t - коэффициент Стьюдента. Доверительные границы Q(Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением. Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении D(Р) рекомендуется осуществлять с использованием критериев и формул, в которых при этом S(x) заменяется на S(
|

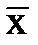 результатов наблюдений хi по формуле
результатов наблюдений хi по формуле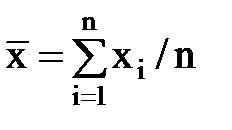
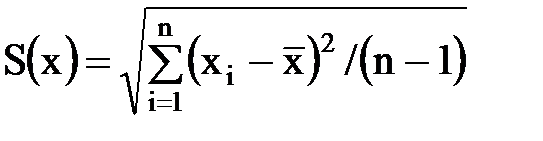
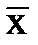 |.
|.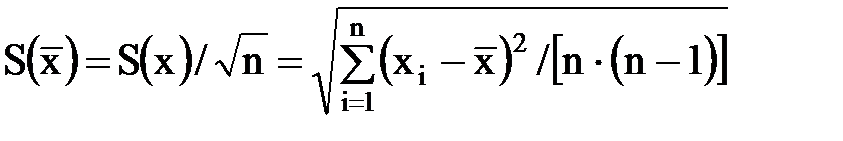 .
.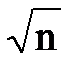 .
.


