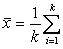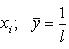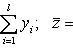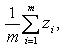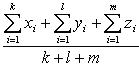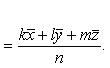Основные свойства средней арифметической
· Если индивидуальные значения признака (варианты), уменьшить (увеличить) в n раз, то среднее значение нового признака соответственно уменьшится или увеличится во столько же. · Если все варианты осредняемого признака уменьшить (увеличить) на число А, то средняя арифметическая соответственно изменится на это же число. · Если вес всех осредняемых вариантов уменьшить (увеличить) в k раз, то средняя арифметическая не изменится. · Сумма отклонений отдельных значений признака от средней арифметической равна нулю. Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака. Пример. Рассмотрим среднюю месячную зарплату работников некоторого предприятия. Пусть, например, в фирме работает 20 человек, зарплата 19 из них составляет 10 000 рублей, а зарплата 10-го, руководителя, - 1 000 000 рублей. Тогда средняя зарплата одного работника на этой фирме будет равна Рассмотрим некоторые свойства среднего арифметического, которые позволяют упростить его вычисление и которые понадобятся при дальнейшем изучении математической статистики. Свойство 1. Среднее арифметическое постоянной величины равно этой постоянной. Пусть при исследовании признака x он n раз принимал одно и то же значение c. Тогда
Свойство 2. Если каждое значение признака Z равно сумме (разности) значений признаков X и Y, то среднее арифметическое признака Z равно сумме (разности) средних арифметических признаков X и Y. Обозначим i -е варианты признаков X, Y, Z через xi, yi, zi. По условию xi + yi = zi. Тогда
Аналогично доказывается свойство и в случае разности. Например, из этого свойства вытекает, что если контрольная работа по геометрии состоит из двух сюжетных задач, то среднее время, которое идет на выполнение контрольной работы, равно сумме средних времен, которые расходуются на выполнение первой и второй задач. Свойство 3. Если ко всем вариантам прибавить одно и то же число, то и к среднему арифметическому будет прибавлено то же число. Пусть
Рассмотренное свойство позволяет значительно упростить вычисление среднего арифметического без использования вычислительных средств, особенно тогда, когда варианты принимают большие значения. Это свойство обосновывает произвольный выбор начала отсчета. Свойство 4. Если все варианты умножить (разделить) на одно и то же число, то среднее арифметическое умножится (разделится) на то же число. Пусть
На основании этого свойства можно изменять единицы, в которых выражаются данные. Свойство 5. Если все частоты умножить (разделить) на одно и то же число, то среднее арифметическое не изменится. Пусть
На основании этого свойства при вычислении среднего частоты можно заменять, например, относительными частотами. Свойство 6. Сумма отклонений вариант от их среднего арифметического равна нулю. Отклонение варианты xi от среднего арифметического
Свойство 7. Сумма квадратов отклонений вариант от их среднего арифметического меньше суммы квадратов отклонений вариант от произвольного числа c на величину В самом деле,
Разность оказалась положительной (при Свойство 8. Среднее арифметическое, вычисленное по данным всех элементов совокупности, равно взвешенному среднему для так называемых частичных средних, т. е. средних, найденных для отдельных частей совокупности, причем частота для каждого частичного среднего равна количеству элементов в соответствующей части совокупности. Пусть совокупность состоит из таких элементов: x 1, x 2,..., xk, y 1, y 2,..., yl, z 1, z 2,..., zm, причем k + l + m = n. Поскольку частичные средние соответственно равны
то общее среднее равно
Например, это свойство дает возможность упростить вычисление среднего арифметического результатов тестирования учащихся классов одной параллели нескольких школ. Для этого достаточно вычислить среднее арифметическое для каждого класса, а затем вычислить среднее этих частичных средних, приняв в качестве их частот количество учащихся в соответствующих классах. Среднее арифметическое позволяет решать задачи, связанные с проверкой гипотез.
|

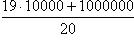
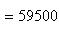 . Хотя среднее и сохранило общую сумму заработной платы, но оно является в данном случае плохим обобщающим показателем: оно плохо характеризует зарплату одного работника на этой фирме. Причина этого кроется в том, что набор данных содержит выброс - 1 000 000 рублей. Среднее оказалось слишком большим для большинства работников и слишком малым для высокооплачиваемого руководителя.
. Хотя среднее и сохранило общую сумму заработной платы, но оно является в данном случае плохим обобщающим показателем: оно плохо характеризует зарплату одного работника на этой фирме. Причина этого кроется в том, что набор данных содержит выброс - 1 000 000 рублей. Среднее оказалось слишком большим для большинства работников и слишком малым для высокооплачиваемого руководителя.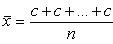
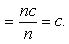

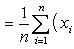
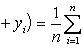

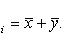
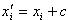 - новые варианты, полученные после прибавления к каждой первоначальной варианте xi одного и того же числа c. Тогда
- новые варианты, полученные после прибавления к каждой первоначальной варианте xi одного и того же числа c. Тогда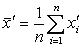
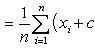
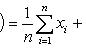


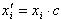 - новые варианты, полученные после умножения каждой первоначальной варианты xi на одно и то же число c. Тогда
- новые варианты, полученные после умножения каждой первоначальной варианты xi на одно и то же число c. Тогда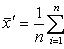

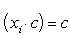
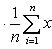
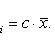
 - новые частоты, полученные после умножения каждой первоначальной частоты ni на одно и то же число c. Тогда
- новые частоты, полученные после умножения каждой первоначальной частоты ni на одно и то же число c. Тогда
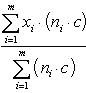

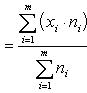

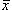 равно разности
равно разности 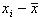 . Тогда
. Тогда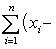
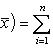
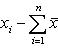
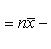
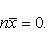
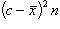 .
.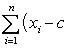
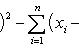
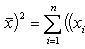
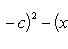

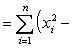
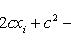
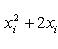
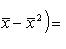
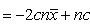
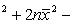
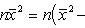

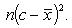
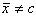 ), поэтому сумма
), поэтому сумма 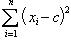 больше суммы
больше суммы 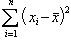 .
.