Доверительным называется интервал  , который с заданной надежностью
, который с заданной надежностью 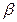 покрывает оцениваемый параметр. Для оценки математического ожидания
покрывает оцениваемый параметр. Для оценки математического ожидания 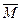 случайной величины X, распределенной по нормальному закону, при известной дисперсии
случайной величины X, распределенной по нормальному закону, при известной дисперсии  служит доверительный интервал
служит доверительный интервал
 , (3.29)
, (3.29)
где  – точность оценки;
– точность оценки;
n – объем выборки;
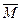 – математическоеожидание;
– математическоеожидание;
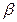 – доверительная вероятность;
– доверительная вероятность;
 – аргумент функции Лапласа;
– аргумент функции Лапласа;
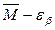 и
и  – границы доверительного интервала.
– границы доверительного интервала.