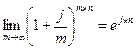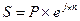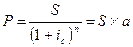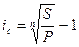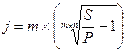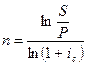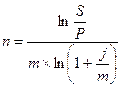Сложные ставки ссудных процентов.
Если после очередного интервала начисления доход (т.е. начисленные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок. Пусть Ø Р — величина первоначальной денежной суммы; Ø F — наращенная сумма; Ø ic — относительная величина годовой ставки сложных ссудных процентов; Ø kн.с. — коэффициент наращения в случае сложных процентов; Ø j — номинальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).
Множитель наращения kн.с. соответственно будет равен:
Сравнивая два последних выражения для коэффициентов наращения, можно видеть, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов. Поэтому, когда возникает возможность выбора между низкой сложной процентной ставкой и более высокой простой, следует отдавать предпочтение первому варианту. Наращение вложенной суммы по простой и сложной процентным ставкам (i = ic = 200%) Если срок ссуды п в годах не является целым числом, множитель наращения определяют по выражению:
где На практике в данном случае часто предпочитают пользоваться формулой (3.1) с соответствующим нецелым показателем степени Предположим теперь, что уровень ставки сложных процентов будет разным на различных интервалах начисления. Пусть n1, n2,…, nN — продолжительность интервалов начисления в годах; i1, i2,…,iN, — годовые ставки процентов, соответствующие данным интервалам. Тогда наращенная сумма в конце первого интервала начисления в соответствии с формулой (1.7), составит: При N интервалах начисления наращенная сумма в конце всего периода начисления составит:
Если все интервалы начисления одинаковы (как и бывает обычно на практике) и ставка сложных процентов одна и та же, формула (3.4) принимает вид:
Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j — годоваяставка, по которой определяется величина ставки процентов, применяемой на каждом интервале начисления. При т равных интервалах начисления и номинальной процентной ставке j эта величина считается равной j/m. Если срок ссуды составляет п лет, то, аналогично формуле (3.1), получаем выражение для определения наращенной суммы:
Здесь mn — общее число интервалов начисления за весь срок ссуды.
Если общее число интервалов начисления не является целым числом (mn — целое число интервалов начисления, l — часть интервала начисления), то выражение (3.6) принимает вид:
Для целого числа периодов начисления используется формула сложных процентов (3.1), а для оставшейся части — формула простых процентов (1.7).
Для расчетов можно использовать известную в математике формулу: Тогда для наращенной суммы получаем:
Здесь
Значения наращенной суммы S можно вычислять с помощью финансового калькулятора, или находя значения ejn и других требуемых величин в специальных таблицах. Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях (т. е. при одинаковых n, j,Р).
Аналогично случаю простых процентов полученные формулы можно преобразовывать, выражая одни величины через другие, в зависимости оттого, что известно, а что требуется найти. Так, из формулы (3.1) получаем:
Напомним, что, как и в случае простых процентов, определение современной величины суммы S называется дисконтированием. Коэффициент дисконтирования а является величиной, обратной коэффициенту наращения. Формула (3.11), а также соответствующие формулы для случая простых ставок ссудного процента и для учетных ставок дают легко понять, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности. Также из формулы (3.1) имеем:
Из формулы (3.6):
Применяя операцию логарифмирования к обеим частям формулы (3.1), получаем:
Подобным же образом из формулы (3.6) получаем формулу:
|

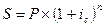
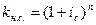
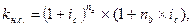
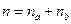 ;
; 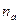 - целое число лет;
- целое число лет; 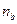 - оставшаяся дробная часть года.
- оставшаяся дробная часть года.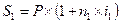 В конце второго интервала:
В конце второго интервала: 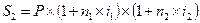 и т.д.
и т.д.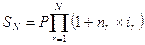
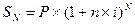
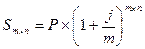
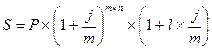
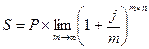
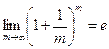 где e = 2,71828... Из этой формулы следует:
где e = 2,71828... Из этой формулы следует: