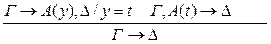Доказательство.
Теорема об устранении сечения (Герхард Генцен, 1936).
Доказательство. Достаточно доказать, что можно устранить верхнее правило сечения. Зафиксируем сложность правила сечения <M, N1+N2>, где М - количество логических связок в формуле сечения, N1 - число секвенций в выводе левой посылки, N2 - число секвенций в выводе правой посылки. <M1, N1>=p1 <M2, N2>=p2 <M1, N1 > < <M2, N2 > По таким парам можно вести индукцию, т.к. множество этих пар обладает свойством фундированности, т.е. любая монотонная убывающая последовательность таких пар является конечной. Пусть р =<M, N1+N2> - сложность. Доказательство ведём по индукции. Индукционное предположение - Все секвенции со сложностью меньше р выводятся без правила сечения.
Докажем для р.
Рассмотрим случаи: 1.С неглавная в левой посылке. 2.С неглавная в правой посылке. 3.С главная в обеих посылках.
1. 1) удаление &:
р:
р* < р
2) удаление Ú: р:
р* < р р** < р
3) удаление
р:
р* < р
4) удаление
р: р* < р
5) удаление р:
р* < р
Надо сохранить чистоту переменных y. При необходимости y выбрать так, чтобы не входили ни в Г, ни в С, ни в
6) удаление р:
р* < р 7-12) Введение &, Ú,
2. 1) введение &: р: р* < р р** < р
2) удаление &:
р:
р* < р
3) введение р: р* < р
4) удаление
р:
р* < р
5) введение Ú: р: р* < р 6) удаление Ú:
р:
р* < р р** < р 7) введение р: р* < р 8) удаление
р: р* < р р** < р 9) введение р:
р* < р 10) удаление р:
р* < р 11) введение р: р* < р
12) удаление р:
р* < р
3. 1)& р: р* < р р** < р 2) Ú
р:
р: 3) р: р* < р 4)
р: р* < р р** < р
5) р: р* < р 6) р: р* < р
Таким образом, теорема об устранении сечения доказана полностью. Следствие 1. Если формула F доказуема, то существует доказательство, состоящее только из подформул формулы F. Следствие 2. СКИП – непротиворечивая система. .
|



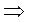
 M1<M2 V M1=M2 & N1<N2
M1<M2 V M1=M2 & N1<N2

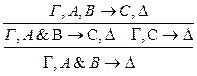
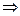 р*:
р*: 

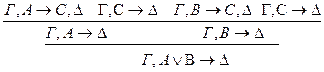 : р**
: р** :
: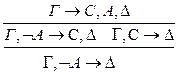
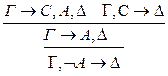
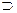 :
:

 :
:

 .
. :
: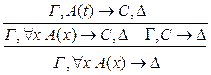
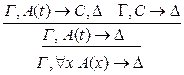

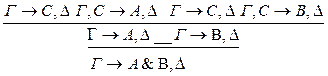 :р**
:р**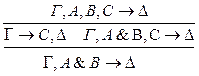
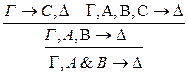


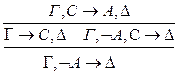
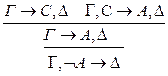
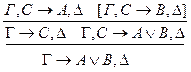
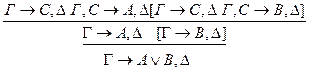
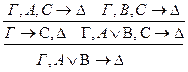
 : р**
: р**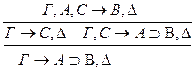


 : р**
: р**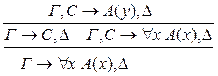

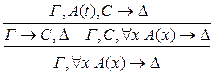


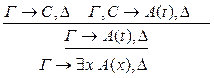
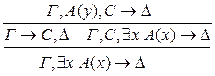

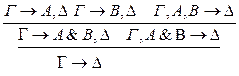
 :р**
:р**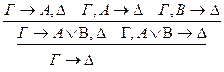
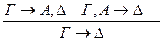 р* < р
р* < р
 р** < р
р** < р

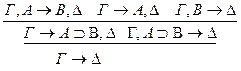
 р**
р**