Теоретическая часть. Известно, что на границе раздела двух прозрачных сред луч света претерпевает преломление, при этом отношение синуса угла падения к синусу угла преломления
Известно, что на границе раздела двух прозрачных сред луч света претерпевает преломление, при этом отношение синуса угла падения к синусу угла преломления есть постоянная для данных двух сред величина, называемая показателем преломления. На основе принципа Гюйгенса для показателя преломления выводится отношение Наблюдения показали, что для любой пары граничащих сред показатель преломления зависит от длины волны падающего света, это явление носит название дисперсии света. Оно проявляется в ряде природных явлений (радуга, цветовая игра бриллиантов) и находит широкое практическое применение в спектральных приборах. Под дисперсией света понимают зависимость показателя преломления от длины волны или частоты: 1.1. Основы элементарной электронной теории дисперсии Рассмотрим элементарную теорию дисперсии света в веществе в соответствии с тем, как это сделал вначале 20-го века Лоренц. Она носит название электронной теории, поскольку в ее основу положено взаимодействие световой волны с электронами вещества. В основе теории Лоренца лежат следующие допущения: главную роль во взаимодействии света с веществом, приводящей к дисперсии, играют внешние, валентные электроны атомов (видимая и ближняя ультрафиолетовые области) и ионы (инфракрасная область); под действием электрической составляющей электромагнитной волны происходит смещение зарядов, что приводит к поляризации атомов и молекул, при этом справедливы соотношения электростатики Используя приведенные три допущения, рассмотрим поведение атома под действием падающей электромагнитной волны, условно полагая атом одноэлектронным. На электрон действуют следующие силы: а) «вынуждающая» внешняя сила:
где б) «упругая» сила, возвращающая его в исходное состояние и определяемая соотношением:
где в) тормозящая сила:
обусловленная действием на электрон соседних атомов, здесь Уравнение динамики для электрона может быть записано в следующем виде:
Введем
Смещение электрона приводит к появлению у атома момента
получаем выражение для диэлектрической проницаемости:
а с учетом соотношения (6.5) и
При более точном решении, если не пренебрегать трением, в знаменателе получится величина Таким образом, мы получили выражение (6.8), в котором показатель преломления вещества Анализ полученного решения позволяет сделать три заключения: – в области – при – при Наглядно это представлено на рис. 6.1, а. С учетом затухания колебаний электрона, т.е. если не пренебрегать «трением», решение несколько меняется: исчезает разрыв в области,
1.2. Количественные характеристики дисперсии вещества Количественной мерой при описании дисперсии света в веществе являются следующие физические величины: а) набор из показателей преломления для фиксированных длин волн, например, б) средняя дисперсия:
в) дисперсия вещества В экспериментальной практике под дисперсией вещества в области
1.3. Количественные характеристики дисперсии спектральных приборов В спектральных измерительных приборах используются весьма точно изготовленные дисперсионные призмы разного типа – от одиночных трехгранных до сложных многогранных или составных. В этом случае принято говорить о дисперсии пробора в целом и использовать следующие характеристики: а) угловая дисперсия прибора б) линейная дисперсия прибора в) разрешающая способность прибора
|

 , где
, где 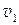 и
и  – скорости распространения света соответственно в первой и второй средах. Вычисленная таким образом величина носит название относительного показателя преломления. Если первой средой является вакуум, то показатель преломления называется абсолютным.
– скорости распространения света соответственно в первой и второй средах. Вычисленная таким образом величина носит название относительного показателя преломления. Если первой средой является вакуум, то показатель преломления называется абсолютным.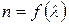 или
или  . Эта функциональная зависимость вытекает из более общей
. Эта функциональная зависимость вытекает из более общей 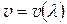 или
или  , что позволяет считать дисперсией света зависимость скорости распространения его в данной среде от частоты или длины волны.
, что позволяет считать дисперсией света зависимость скорости распространения его в данной среде от частоты или длины волны. ; в соответствии с теорией Максвелла относительный показатель преломления света связан с электрическими и магнитными свойствами среды соотношением
; в соответствии с теорией Максвелла относительный показатель преломления света связан с электрическими и магнитными свойствами среды соотношением  , а поскольку для большинства веществ
, а поскольку для большинства веществ  , то будем считать, что
, то будем считать, что  .
. (6.1)
(6.1) – напряженность электрической составляющей электромагнитной волны;
– напряженность электрической составляющей электромагнитной волны;  – заряд электрона;
– заряд электрона;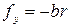 (6.2)
(6.2)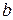 – коэффициент «упругости»,
– коэффициент «упругости», 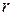 – смещение электрона от положения равновесия;
– смещение электрона от положения равновесия; (6.3)
(6.3)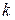 – коэффициент «трения»,
– коэффициент «трения»,  – скорость движения электрона.
– скорость движения электрона.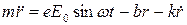 (6.4)
(6.4)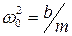 и, полагая трение ничтожно малым
и, полагая трение ничтожно малым  , получим дифференциальное уравнение второй степени, решением которого является:
, получим дифференциальное уравнение второй степени, решением которого является: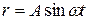 , где
, где 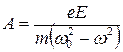 (6.5)
(6.5) , а синхронное смещение
, а синхронное смещение  электронов единицы объема вещества создает поляризуемость
электронов единицы объема вещества создает поляризуемость 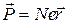 . Используя известное из электростатики соотношение
. Используя известное из электростатики соотношение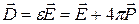 , (6.6)
, (6.6)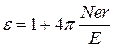 , (6.7)
, (6.7) получаем:
получаем: . (6.8)
. (6.8) .
. зависит от частоты
зависит от частоты 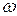 падающего света. Сюда входят такие характеристики самого вещества, как концентрация атомов, собственная частота колебаний электронов
падающего света. Сюда входят такие характеристики самого вещества, как концентрация атомов, собственная частота колебаний электронов 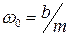 , масса электронов
, масса электронов  (или иона).
(или иона).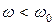 показатель преломления больше 1 и с увеличением частоты падающего света растет;
показатель преломления больше 1 и с увеличением частоты падающего света растет; показатель преломления принимает значение
показатель преломления принимает значение  ;
;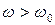 показатель преломления меньше 1 и с увеличением частоты растет, стремясь к 1.
показатель преломления меньше 1 и с увеличением частоты растет, стремясь к 1.
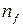 для
для  (синяя линия водорода) и
(синяя линия водорода) и 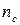 для
для  (красная линия водорода);
(красная линия водорода); ;
;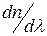 – скорость изменения показателя преломления в данном вещества, зависящая от рода вещества и спектрального интервала. Она вводится из-за сложного нелинейного характера зависимости
– скорость изменения показателя преломления в данном вещества, зависящая от рода вещества и спектрального интервала. Она вводится из-за сложного нелинейного характера зависимости 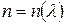 . В области пропускания вещества, т.е. вдали от резонансных частот
. В области пропускания вещества, т.е. вдали от резонансных частот 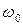 , дисперсия
, дисперсия 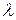 понимают отношение
понимают отношение 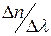 , характерное для данной длины волны. В ее окрестности выбирается интервал
, характерное для данной длины волны. В ее окрестности выбирается интервал 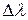 и соответствующая ему величина
и соответствующая ему величина  .
.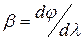 , где
, где 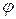 – угол отклонения луча от оси прибора;
– угол отклонения луча от оси прибора; , где
, где 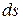 – расстояние между изображением спектральных линий в фокальной плоскости выходного коллиматора;
– расстояние между изображением спектральных линий в фокальной плоскости выходного коллиматора; , где
, где 


