Кинематические параметры движения точки
Пусть имеется две декартовых системы координат в трехмерном евклидовом пространстве, которые обозначим индексами Матрица преобразования координат имеет следующую структуру:
где
Используя однородные координаты и матрицы их преобразования, можно записать следующие выражения:
Используя выражения для матриц преобразования однородных координат и выражения для параметров углового движения систем координат, выражение (2) можно записать в следующем виде
или окончательно
Равенство (4) выражает теорему о сложении скоростей, которую в теоретической механике, опуская операции преобразования векторов к единой системе координат, принято записывать в следующем виде
Используя выражения для матриц преобразования однородных координат и выражения для параметров углового движения систем координат, выражение (3) можно записать в следующем виде
или окончательно
Равенство (5) выражает теорему Кориолиса о сложении ускорений, которую в теоретической механике, опуская операции преобразования векторов к единой системе координат, принято записывать в следующем виде
|

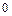 и
и 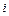 . Будем считать систему координат с индексом
. Будем считать систему координат с индексом 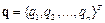 . Положение некоторой произвольной точки в системе координат
. Положение некоторой произвольной точки в системе координат 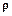 , а положение этой же точки в системе координат
, а положение этой же точки в системе координат 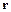 .
.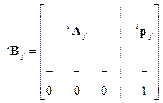 , (2)
, (2)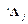 - матрица направляющих косинусов, или матрица поворота осей, при переходе от
- матрица направляющих косинусов, или матрица поворота осей, при переходе от 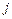 -й системы координат к
-й системы координат к 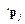 - вектор смещения центра
- вектор смещения центра 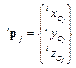 .
. ; (1)
; (1) ; (2)
; (2) . (3)
. (3)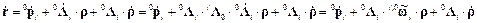 ;
;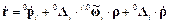 . (4)
. (4)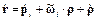 .
.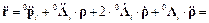

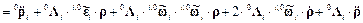 ;
;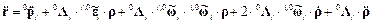 . (5)
. (5) .
.


