Основы зонной теории твердых тел. Распределение Ферми-Дирака.
В процессе образования твердого тела электронные энергетические уровни отдельных атомов из-за взаимодействия электронов смещаются и образуют энергетические полосы (разрешенные зоны), чередующиеся с уровнями энергий, значений которых электроны принимать не могут (запрещенные зоны). Энергетическая ширина как разрешенной так и запрещенной зон имеет порядок ~10-19 Дж. Энергетический зазор между отдельными уровнями разрешенных зон составляет ~10-41 Дж, поэтому обычно считают, что энергетический спектр электронов внутри разрешенной зоны практически непрерывен. Наиболее сильно расщепляются энергетические уровни валентных электронов, образуя так называемые валентную зону (ВЗ) и зону проводимости (ЗП). Вероятность того, что осотояние с энергией Е при температуре Т занято электроном, определяется, как известно, функцией Ферми – Дирака:
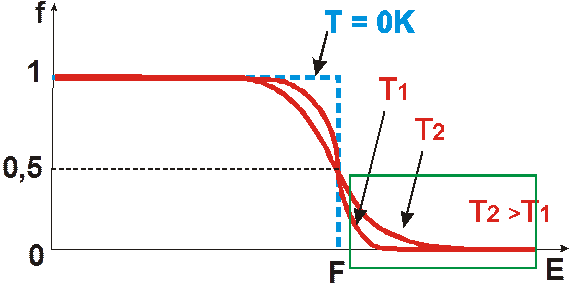
Величину EF называют энергией Ферми (уровнем Ферми). Легко видеть, что при Т=0 К функция
С хорошим приближением можно считать, что D(E) имеет вид:
где m* - эффективная масса электрона, EC – энергия, соответствующая дну зоны проводимости. Плотность заполнения электронами энергетической зоны описывается, таким образом, следующей формулой:
Как видно из (2.1) и рис. 2 вероятность нахождения частицы на уровне с энергией EF всегда равна
Используя сделанные допущения, возможно рассчитать количество электронов находящихся в заданном энергетическом интервале ΔE = E2 -E1:
где D(E) – распределение плотности энергетических состояний по энергиям, ω(E) – вероятность нахождения электрона на уровне с энергией E, В качестве примера на рис. 2.1 показано, как используя функцию распределения ω(E) и функцию плотности состояния (D(E)~E1/2) определить распределение электронов по энергиям в металле или вырожденном полупроводнике.
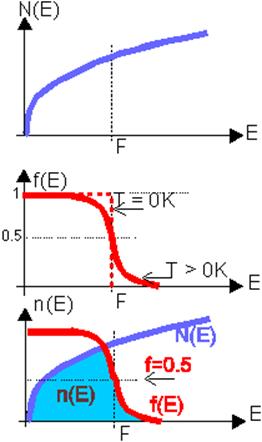
Рис. 2.1. Схема расчета распределения электронов по энергиям в металле (или вырожденном полупроводнике) при использовании зависимостей D(E), ω(E); n(E)=D(E)ω(E)
На рис. 2.1 (нижний график) показано распределение электронов характерное для металлов или вырожденных полупроводников, т.е полупроводников имеющих настолько высокую концентрацию примесей, что в них уровень Ферми попадает в разрешенную зону и их проводимость становится близкой к металлической. Из распределения рис. 2 можно сделать один важный вывод, то в проводимости металлов могут участвовать не все электроны, а только те энергия которых лежат вблизи уровня Ферми (в объемном случае вблизи поверхности Ферми). Действительно, в электрическом поле электрон приобретает энергию, следовательно, он должен перемещаться на уровень расположенный выше его начального состояния, а сделать это возможно только в том случае, если лежащий над ним уровень не занят (запрет Паули), такая ситуация имеет место только для электронов расположенных в энергетической области непосредственно примыкающей к уровню Ферми.
|

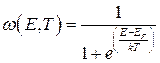 (2.1)
(2.1)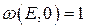 - если Е<ЕF; и равна нулю – если Е>ЕF. График этой функции изображен на рис. 2. При любой другой температуре энергия Ферми совпадает с энергией того уровня, вероятность заполнения которого равна 0,5. Если бы энергетические уровни в зоне были распределены равномерно то, число электронов, имеющих энергию Еi в небольшом интервале dE, определялось бы из функции распределения (2.1). Однако вблизи дна зоны проводимости энергетические уровни расположены реже, чем в верхней её части. Распределение энергетических уровней характеризуют функцией D(E) – функцией плотности энергетических состояний.
- если Е<ЕF; и равна нулю – если Е>ЕF. График этой функции изображен на рис. 2. При любой другой температуре энергия Ферми совпадает с энергией того уровня, вероятность заполнения которого равна 0,5. Если бы энергетические уровни в зоне были распределены равномерно то, число электронов, имеющих энергию Еi в небольшом интервале dE, определялось бы из функции распределения (2.1). Однако вблизи дна зоны проводимости энергетические уровни расположены реже, чем в верхней её части. Распределение энергетических уровней характеризуют функцией D(E) – функцией плотности энергетических состояний.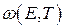
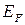
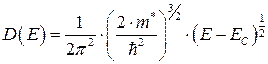 (2.2)
(2.2)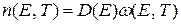 (2.2а)
(2.2а)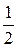 при всех температурах. В то же время по мере роста температуры вероятность появления частиц выше уровня Ферми возрастает. При температурах отличных от нуля, если E - EF > kT, то функция Ферми-Дирака хорошо представляется экспоненциальной зависимостью (область в квадрате на рис. 2). Соответствующее распределение называется распределением Больцмана:
при всех температурах. В то же время по мере роста температуры вероятность появления частиц выше уровня Ферми возрастает. При температурах отличных от нуля, если E - EF > kT, то функция Ферми-Дирака хорошо представляется экспоненциальной зависимостью (область в квадрате на рис. 2). Соответствующее распределение называется распределением Больцмана: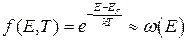 (2.3)
(2.3)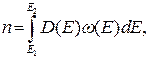 (2.4)
(2.4)


