Составитель: канд. техн. наук доц. Л.А. Федорова, ассистент Гладкий Н.А.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский Государственный университет аэрокосмического приборостроения
ИССЛЕДОВАНИЕ ДИСПЕРСИИ И ЗАТУХАНИЯ ВОЛН В ВОЛНОВОДАХ
Методические указания к выполнению лабораторной работы
Санкт-Петербург
Составитель: канд. техн. наук доц. Л.А. Федорова, ассистент Гладкий Н.А. Рецензент: канд. техн. наук доц. А.Ю.Гулевитский В настоящих методических указаниях рассмотрены явления дисперсии и затухания электромагнитных волн в волноводе прямоугольного сечения. Приводятся краткие сведения из теории и основные аналитические выражения для расчета дисперсных характеристик волновода. Излагается методика я порядок выполнения экспериментальных исследований на прямоугольном волноводе, дается описание лабораторной установки. Методические указания предназначены для студентов дневного, вечернего и заочного факультетов, изучающих курс «Электродинамика и РРВ» «Техническая электродинамика» «Электродинамика и техника СВЧ» «Основы электродинамики и РРВ» «Электромагнитные поля и волны» по специальностям 2007, 2016, 2008 2013, 2014, 1312 и направлениям 5520 и 5525. Подготовлены к публикации кафедрой антенн и эксплуатации РЭА по рекомендации методической комиссии факультета радиотехники, электроники и связи Санкт-Петербургского государственного университета аэрокосмического приборостроения.
Ó Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2002
Лицензия ЛР № 020341 от 07. 05. 97
Редакционно- издательский отдел Отдел оперативной полиграфии СПбГУАП 190000, Санкт-Петербург, ул. Б.Морская,67
Лабораторная работа. Исследование дисперсии и затухания волн в волноводах. Цель работы: 1.Изучить явление дисперсии и затухания волн в волноводе прямоугольного сечения. 2.Изучить метода измерения параметров, характеризующих дисперсию и затухание. 3.Исследовать экспериментально изменение фазовой и групповой скоростей, а также затухания в зависимости от частоты генерируемых колебаний. 4.Исследовать математически зависимости затухания, фазовой и групповой скоростей от поперечных размеров волновода, диэлектрической проницаемости заполнения и удельной проводимости стенок в заданном частотном диапазоне. 1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Электромагнитные волны, распространяющиеся в линиях передачи, делятся на поперечные волны, электрические и магнитные. Поперечными или Т-волнами называются волны, у которых векторы E электрического и H магнитного полей лежат в плоскости, перпендикулярной направлению распространения. Электрическими или E-волнами называют волны, у которых вектор электрического поля E помимо поперечных составляющих по отношении к направлению распространения имеет в продольную составляющую E Z. Продольная же составляющая H Z равна нулю. Волны типа E иногда называют поперечными магнитными волнами ТМ. Магнитными или Н-волнами называют волны, у которых вектор магнитного поля H помимо поперечных составляющих имеет продольную составляющую H Z Продольная же составляющая электрического поля Е Z равна нулю, поэтому Н-волны иногда называют поперечными электрическими волнами или волнами ТЕ. В прямоугольном волноводе в общем случае может существовать бесконечное множество волн типа Emn и Hmn, отличающихся значениями индексов m и n, которые определяют число полуволн поля, укладывающихся по широкой стенке a и узкой стенке b соответственно. Каждая из этих волн существует совершенно независимо друг от друга и имеет свою критическую длину волны
Условием распространения волн Emn иHmn в прямоугольном волноводе с рабочей длиной волны Диапазон длин волн, при которых длина волны больше критической длины волны, называют областью отсечки, так как распространения волны не происходит. Волну с наибольшей величиной Низший тип волны обеспечивает наименьшие размеры поперечного сечения, а следовательно, наименьшие габариты и вес волновода для заданной длины волны (a Поясним физический смысл критической длины волны, используя концепцию парциальных волн, распространяющихся по волноводу путем многократных переотражений от боковых стенок волновода. Прямоугольный волновод с волной типа Н10 имеет одну составляющую Еу электрического поля и две составляющие Hx и Hz магнитного поля (см. рис.1).
Рис.1. Такую волну можно представить в виде двух плоских Т-волн. Одна из них распространяется вдоль оси
Значения электрического и магнитного полей во внутренней полости волновода будут определяться как геометрическая сумма падающих и отраженных волн, образуя максимумы там, где поля складываются в фазе, и минимумы – при противофазном сложении. При этом на проводящей поверхности волновода выполняются граничные условия: касательные составляющие электрического поля и нормальные составляющие магнитного поля равны нулю. Для волн Нmo минимумы напряженности электрического доля E образуются на узких стенках волновода при любом расстоянии a между ними. Для любого заданного размера широкой стенки a всегда выполняется равенство а = m где cos Если волновод заполнен диэлектриком, относительные диэлектрическая
Применение диэлектрического заполнения позволяет использовать волновод при неизменных габаритах на более низких частотах. Однако необходимо учесть, что в большинстве своем диэлектрики имеют значительные потери в области сверхвысоких частот и обладают низкой температурной стойкостью, что ограничивает их применение. Относительную магнитную проницаемость диэлектриков можно в практических случаях считать равной единице, исключение составляют ферромагнетики. Важными параметрами, характеризующими распространение волны в волноводе, являются затухание V = При воздушной заполнении Найдем величину фазовой скорости VФ. Из треугольника АВС следует: AC = AB /sin Vф = С /sin Так как АС больше АВ, а время распространения t одинаково, то фазовая скорость волны в волноводе больше скорости волны в свободном пространстве (больше скорости света). Если принять время t равным периоду Т, то путь АВ равен длине волны
|

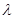 кр, которая связана с поперечными размерами прямоугольного волновода соотношением
кр, которая связана с поперечными размерами прямоугольного волновода соотношением .
. кр.
кр.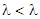 крН10) и (
крН10) и ( 2 a) и (2 b
2 a) и (2 b  ).
).
 волновода и имеет составляющие поля Ey и Нx, связанные с вектором Умова-Пойнтинга соотношением Пz=[Ey х Hx]. Другая Т-волна распространяется в направлении оси
волновода и имеет составляющие поля Ey и Нx, связанные с вектором Умова-Пойнтинга соотношением Пz=[Ey х Hx]. Другая Т-волна распространяется в направлении оси  и имеет вектор Умова-Пойнтинга Пх = [Ey x Hz]. В результате сложения двух плоских Т-волн энергия будет переноситься в направлении Ппад, определяемом сложением векторов Пz и Пx. В таком случае естественно предположить, что электромагнитная волна Т распространяется по волноводу путем многократного переотражения от боковых стенок волновода. В этом случае вектора Ey и Hпад. волны Т должны находиться в плоскостях, перпендикулярных соответствующим участкам ломаной линии, определяющей направление падения П пад. на стенку под углом
и имеет вектор Умова-Пойнтинга Пх = [Ey x Hz]. В результате сложения двух плоских Т-волн энергия будет переноситься в направлении Ппад, определяемом сложением векторов Пz и Пx. В таком случае естественно предположить, что электромагнитная волна Т распространяется по волноводу путем многократного переотражения от боковых стенок волновода. В этом случае вектора Ey и Hпад. волны Т должны находиться в плоскостях, перпендикулярных соответствующим участкам ломаной линии, определяющей направление падения П пад. на стенку под углом 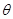 . Отражается волна в строго определенном направлении Потр. в соответствии с законом Снеллиуса – угол падения равен углу отражения [1, 2].
. Отражается волна в строго определенном направлении Потр. в соответствии с законом Снеллиуса – угол падения равен углу отражения [1, 2].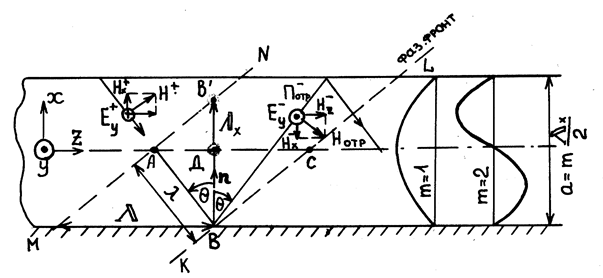
 x / 2 = m
x / 2 = m  должен увеличиваться, что ведет к уменьшению cos
должен увеличиваться, что ведет к уменьшению cos  Тогда из формулы (2) получим
Тогда из формулы (2) получим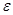 и магнитная
и магнитная  проницаемости которого отличны от единицы, то длина волны
проницаемости которого отличны от единицы, то длина волны  .
.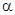 , а также фазовая Vф и групповая Vгр скорости. Рассмотрим плоскую электромагнитную Т-волну, падающую на боковую стенку волновода под углом
, а также фазовая Vф и групповая Vгр скорости. Рассмотрим плоскую электромагнитную Т-волну, падающую на боковую стенку волновода под углом 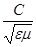 . (4)
. (4) и
и 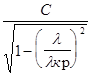 . (5)
. (5) =
=  . (6)
. (6)


