Представление дерева в виде списка

Деревья

1. Общие положения(Повторение)

Представление дерева

Двоичные деревья

Сбалансированные деревья

Дерево — это совокупность элементов, называемых узлами (при этом один из них определен как корень), и отношений (родительский–дочерний), образующих иерархическую структуру узлов. Узлы могут являться величинами любого простого или структурированного типа, за исключением файлового. Узлы, которые не имеют ни одного последующего узла, называются листьями.

По величине степени дерева(количество дуг из вершины) можно выделить два типа деревьев:

- двоичные - степень дерева не более двух;

- сильноветвящиеся – степень дерева произвольная.

Если двоичное дерево организовано таким образом, что для каждого узла все ключи (значения узлов) его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева больше. Такой способ построения дерева называется деревом поиска или двоичным упорядоченным деревом.

Представление дерева в виде списка

Для дерева произвольной степени список дерева можно представить следующим образом

 

 

 

Указатель на дерево

 

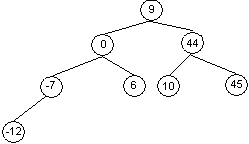
Тогда запишем указатель на вершину(корень) дерева

type

PTree=^TTree;

TTree=record

Data:TypeElement;{поле данных}

Chids,Next:PTree;{указатели на потомков и на следующий}

end;

В двоичном (бинарном) дереве каждый узел может быть связан не более чем двумя другими узлами. Рекурсивно двоичное дерево определяется так: двоичное дерево бывает либо пустым (не содержит ни одного узла), либо содержит узел, называемый корнем, а также два независимых поддерева — левое поддерево и правое поддерево.

Двоичное дерево поиска может быть либо пустым, либо оно обладает таким свойством, что корневой элемент имеет большее значение узла, чем любой элемент в левом поддереве, и меньшее или равное, чем элементы в правом поддереве. Указанное свойство называется характеристическим свойством двоичного дерева поиска и выполняется для любого узла такого дерева, включая корень. Далее будем рассматривать только двоичные деревья поиска. Такое название двоичные деревья поиска получили по той причине, что скорость поиска в них примерно такая же, что и в отсортированных массивах: O (n) = C • log₂ n (в худшем случае O (n) = n).

Пример. Для набора данных 9, 44, 0, –7, 10, 6, –12, 45 построить двоичное дерево поиска.

Согласно определению двоичного дерева поиска число 9 помещаем в корень, все значения, меньшие его — на левое поддерево, большие или равные — на правое. В каждом поддереве очередной элемент можно рассматривать как корень и действовать по тому же алгоритму. В итоге получаем

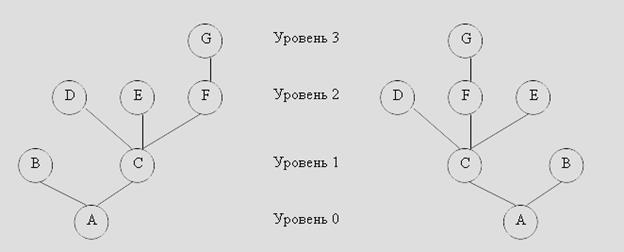
Необходимо отметить, что деревья – это одна из наиболее важных нелинейных структур, которые встречаются при работе с компьютерными алгоритмами, их используют при анализе электрических цепей, математических формул, для организации информации в системах управления базами данных и для представления синтаксических структур в компиляторах.

Вообще говоря, древовидная структура задает для элементов дерева (узлов) отношение «ветвления», которое во многом напоминает строение обычного дерева.

Формально дерево (tree) определяется как конечное множество T одного или более узлов.

При этом каждый узел дерева является корнем некоторого поддерева данного дерева. Количество поддеревьев узла называется степенью этого узла. Узел с нулевой степенью называется концевым узлом или листом. Не концевой узел называется узлом ветвления. Каждый узел имеет уровень, который определяется следующим образом: уровень корня дерева равен нулю, а уровень любого другого узла на единицу выше, чем уровень корня ближайшего поддерева, содержащего данный узел.

Рассмотрим эти понятия на примере дерева с семью узлами (см. рисунок). Узлы часто изображаются буквами, они так же, как и элементы списков могут быть элементами любого типа.

 

 

Узел A является корнем, который имеет два поддерева { B } и { C, D, E, F, G }. Корнем дерева{ C, D, E, F, G } является узел C. Уровень узла C равен 1 по отношению ко всему дереву. Он имеет три поддерева { D }, { E }и { F, G }, поэтому степень узла C равна 3. Концевыми узлами (листьями) являются узлы B, D, E, G.

Путем из узла n₁ в узел n_k называется последовательность узлов n ₁, n ₂, … n _k. Узел n_i является родителем узла n_{i +1} . Длиной пути называется число, на единицу меньшее числа узлов, составляющего этот путь. Таким образом, путем нулевой длины будет путь из любого узла к самому себе. Например, на рисунке путем длины 2 будет путь от узла A к узлу F или от узла C к узлу G.

Если существует путь из узла a в узел b, то в этом случае узел a называется предком узла b, а узел b – потомком узла a. Отметим, что любой узел одновременно является предком и потомком самого себя. Например, на рисунке предками узла G будут сам узел G и узлы F, C и A. Потомками узла C будут являться сам узел C и узлы D, T, F, G. В дереве только корень не имеет предков, а листья не имеют потомков.

Предок узла, имеющий уровень на единицу меньше уровня самого узла, называется родителем. Потомки узла, уровень которых на единицу больше относительно самого узла, называются сыновьями или детьми. Узлы, являющиеся сыновьями одного родителя, принято называть братьями.

Высотой узла дерева называется длина самого длинного пути от этого узла до какого-либо листа. Глубина узла определяется как длина пути от корня до этого узла.

Лес – это множество (обычно упорядоченное), содержащее несколько непересекающихся деревьев. Узлы дерева при условии исключения корня образуют лес.

Порядок узлов

 

 

Если в определении дерева имеет значение порядок поддеревьев T₁, T ₂,... T _m, то дерево является упорядоченным.

Сыновья узла обычно упорядочиваются слева направо. Поэтому деревья, приведенные на рисунке, являются различными.

Если порядок сыновей игнорируется, то такое дерево называется неупорядоченным. Далее будем неявно предполагать, что все рассматриваемые деревья являются упорядоченными, если явно не указано обратное.

Выделяют следующие типовые операции над двоичными деревьями поиска:

· добавление элемента в дерево;

· удаление элемента из дерева;

· обход дерева (для печати элементов и т.д.);

· поиск в дереве.