Прямолинейные колебания точки
§ 2. Свободные незатухающие колебания точки под действием линейной восстанавливающей силы
Свободные незатухающие колебания точки можно изучить на следующей механической модели. Рассмотрим тело массой m которое может скользить по гладкой горизонтальной плоскости. Прикрепим тело к пружине с коэффициентом жесткости, равным С. Совместим начало координат с центром тяжести неподвижного груза (пружина не деформирована) и направим ось Оx параллельно опорной плоскости. Пусть в начальный момент (t0=0) груз отклонен от положения равновесия на расстояние x0 и ему сообщена начальная скорость Fx=-cx. Дифференциальное уравнение движения груза
или
Начальные условия
Решение уравнения (2.1), удовлетворяющее начальным условиям (2.2), можно записать в следующей форме:
где
Параметры А (амплитуда), К (частота) и Уравнение (2.3) описывает свободные гармонические колебания точки с периодом
Вопросы для самоконтроля 1. Каково математическое выражение линейной восстанавливающей силы? 2. Запишите дифференциальное уравнение движения точки под действием восстанавливающей силы. 3. Какой вид имеет общее решение этого уравнения? 4. Как формулируются начальные условия? 5. Представьте общее решение дифференциального уравнения в амплитудной форме. Как выражаются постоянные А и 6. Разъясните физический смысл постоянных А, 7. Начертите график свободных гармонических колебаний. 8. При каких начальных условиях амплитуда А больше начального отклонения x0? 9. Запишите выражение периода свободных (гармонических) колебаний. Зависит ли он от начальных условий? Покажите на графике колебаний период Т. 10. Как влияет постоянная сила на свободные гармонические колебания? 11. Что называется статическим отклонением точки? Почему удобно помещать начало координат в положение статического равновесия? 12. Как выражается период свободных колебаний точки через статическое отклонение? Пример 1. Неупругий удар груза о балку Груз Q, падая с высоты h=1 м без начальной скорости, ударяется об упругую горизонтальную балку АВ в ее середине; концы балки закреплены. Написать уравнение дальнейшего движения груза на балку, отнеся движение к оси, проведенной вертикально вниз из положения статического равновесия груза на балке, если статический прогиб балки в ее середине при указанной нагрузке равен 0,5 см., массой балки пренебрегаем. Определить наибольшее давление груза на балку и динамический коэффициент. Будем предполагать, что после удара груз не отделяется от балки (абсолютно неупругий удар). Рассмотрим движение груза. Отметим три точки: О1 – положение середины недеформированной балки; О – положение статического равновесия груза на балке; М – текущее положение груза. Поместим начало координат в точке О. Ось Оx направим по вертикали вниз. Текущее положение груза определим координатой x относительно точки О. В положении М на груз действуют две силы: сила тяжести Q и упругая реакция балки, проекция которой на ось x равна:
Здесь С – коэффициент жесткости, ƒ – статический прогиб в середине балки. Запишем дифференциальное уравнение движения груза:
Так как в положении статического равновесия имеет место равенство Q=cƒ,
то (2.6) можно переписать в виде (2.1). Уравнение (2.1) описывает движение груза с момента соприкосновения его с балкой в точке О1. Этот момент мы примем за начало отсчета времени (t0=0). Тогда начальное отклонение x0=-ƒ, а начальная скорость груза
X0=x(0)=-ƒ;
Общее решение уравнения (2.1) можно записать в виде (2.3). Остается определить А и α. Для нахождения численных значений параметров А и α предварительно вычислим
Используя условия задачи и принимая во внимания (2.4) и (2.7) –(2.8), находим
Закон движения (2.3) принимает вид
Следовательно, груз совершает свободные гармонические колебания; частота колебаний Определим теперь давление груза на балку. Оно равно упругой реакции балки
F=c(ƒ+x)+cƒ+cAsin(кƒ+α).
Максимальное значение силы
Используя соотношения
получаем
где
Величину H называют динамическим коэффициентом, который показывает, во сколько раз максимальная динамическая нагрузка превышает соответствующую статическую. При числовых данных нашей задачи
Как видно динамическое воздействие груза на балку может в десятки раз превышать статическое. Это обстоятельство необходимо учитывать при расчете балки на прочность. После определения динамического коэффициента расчет балки производится на статическую нагрузку Q*=HQ. Упражнения. 1. Как изменяются амплитуда, период, частота колебаний, если: а) массу увеличить в 4 раза; б) массу точки уменьшить в 9 раз; в) жесткость пружины С увеличить (уменьшить) в 2 раза? 2. Под действием груза, подвешенного к концу пружины, она получила статическое удлинение ƒ=5 см. Записать начальные условия движения груза, поместив начало координат в положение статического равновесия и направив ось Оx вертикально вниз, если известно, что в начальный момент: а) пружина растянута на 7 см и груз отпущен без начальной скорости; б) груз находится в положении статического равновесия и ему сообщена начальная скорость, направленная вертикально вниз, равная 4 см/сек; в) пружина сжата на 1 см и грузу сообщена начальная скорость 8 см/сек, направленная вертикально вверх. 3. Решите задачи 32.2; 32.10;32.11; 32.24; 32.13; 32.16; 32.17; 32.6; 32.28 из (7)
|

 в направлении оси Ox. Движение груза вдоль оси Ox будет проходить под действием восстанавливающей силы F, проекция которой на ось Ox
в направлении оси Ox. Движение груза вдоль оси Ox будет проходить под действием восстанавливающей силы F, проекция которой на ось Ox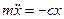
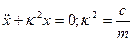 . (2.1)
. (2.1)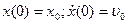 . (2.2)
. (2.2)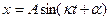 , (2.3)
, (2.3)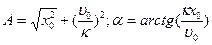 . (2.4)
. (2.4) (начальная фаза) являются основными физическими характеристиками рассматриваемого движения.
(начальная фаза) являются основными физическими характеристиками рассматриваемого движения.
 . (2.5)
. (2.5)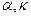 .
.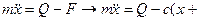 ƒ). (2.6)
ƒ). (2.6) . Решение задачи сводится к интегрированию уравнения (2.1) при начальных условиях:
. Решение задачи сводится к интегрированию уравнения (2.1) при начальных условиях: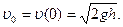

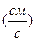 . (2.8)
. (2.8)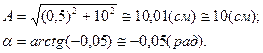
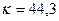 с-1, амплитуда А = 10 см, начальная фаза α=0,05 рад.
с-1, амплитуда А = 10 см, начальная фаза α=0,05 рад.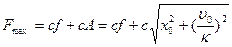 .
. ,
,
 .
. .
.


