Влияние сил сопротивления на свободные колебания материальной точки
Воспользуемся вновь механической моделью §2. Движение материальной точки под действием восстанавливающей силы F=-cx и силы сопротивления
где
Характер решения уравнения (3.1) зависит от дискриминанта Д характеристического уравнения, составленного для (3.1)
Могут представиться следующие случаи: 1. 2. Д<0 - условно периодическое движение (затухающие колебания).
При Д<0 вводят обозначение
В этом случае решение уравнения (3.1) представимо в следующем виде:
Здесь
Быстрота затухания колебаний характеризуется декрементом. Рассмотрим последовательность амплитуд
Величина
Вопросы для самоконтроля 1. Запишите дифференциальное уравнение движения точки под действием линейной восстанавливающей силы и силы сопротивления, пропорциональной первой степени скорости. 2. Какой вид имеет общее решение дифференциального уравнения движения точки под действием восстанавливающей силы и силы сопротивления, пропорциональной скорости для случаев 3. Представьте общее решение дифференциального уравнения (для случая 4. Выразите новые произвольные постоянные A0,α через начальные условия. 5. Начертите график затухающих колебаний. Запишите выражение условного периода этих колебаний Т*. Покажите Т* на графике. 6. Как зависит период Т* от коэффициента сопротивления? 7. По какому закону убывает амплитуда затухающих колебаний? 8. Что называется декрементом затухания? Логарифмическим декрементом? 9. Постройте графики апериодических движений точки. Во многих отраслях техники, где колебания играют отрицательную роль, возникает проблема гашения колебаний. Для ее решения используются различные устройства, среди которых широко применяются демпферы.
Пример. Гидравлический демпфер
Гидравлический демпфер представляет собой поршень массой m, движущийся в вязкой жидкости. Найти закон движения поршня, зная, что в начальный момент (t0=0) поршень отклонен от положения равновесия на h=0,5 см и отпущен без начальной скорости. Определить число полупериодов колебаний, необходимое для того, чтобы отклонение поршня от положения равновесия уменьшилось в 50 раз. Коэффициент жесткости пружины С=3 кг/см, вес поршня Q=2, 73 кг, коэффициент вязкого сопротивления Пусть O1- положение центра тяжести поршня при недеформированной пружине; О – положение статического равновесия. Поместим начало отсчета в точку О и направим ось x вертикально вниз. Рассмотрим произвольное положение груза (точка М), которое определяется координатой x. Укажем все силы, приложенные к грузу в этом положении: силу веса З, восстанавливающую силу F и силу сопротивления среды R. Проекции этих сил на ось x есть соответственно
Запишем дифференциальное уравнение движения поршня в проекции на ось x
Так как в положении статического равновесия P=cƒ, то уравнение (3.6) примет вид (3.1), где введены обозначения (3.2). Уравнение (3.1) надо проинтегрировать при следующих начальных условиях:
Ниже, производя вычисления, мы убедимся, что Для определения постоянных А и α используем начальные условия (3.7). Дифференцируя по времени (3.4), получаем
Из (3.1), (3.7) и (3.8) следует
Откуда
Для определения числовых значений параметров А0,Н и α вычисляем
Имеем
Легко проверить, что, полагая
Определим теперь число полупериодов колебаний, необходимое для практического погашения колебаний. Так как
Отсюда, принимая во внимание (3.5), находим
По условия задачи
Следовательно, можно принять n=9. Отметим, что распоряжаясь параметрами
Упражнения
1. Груз весом Р=98 кг, подвешенный к концу пружины, движется в жидкости. Коэффициент жидкости пружины С=10 г/см. Сила сопротивления движению пропорциональна первой степени скорости. Каким (периодическим или апериодическим) будет движение груза, если: а) μ=1,6 г.с/см; б) μ=5,2 г.с/см; в) μ=2 г.с/см? Найти уравнение движения груза во всех этих случаях, если в начальный момент груз был смещен из положения статического равновесия вниз на 6 см и ему была сообщена начальная скорость 2. Решить задачи: № 32.62, 32.63, 32.64, 32.67 из (7).
|

 описывается дифференциальным уравнением
описывается дифференциальным уравнением , (3.1)
, (3.1)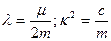 . (3.2)
. (3.2)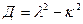 .
.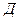 ≥0 - апериодическое движение;
≥0 - апериодическое движение;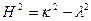 . (3.3)
. (3.3)
 . (3.4)
. (3.4)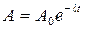 - амплитуда, Н- частота, α- начальная фаза затухающих колебаний. Движение, представленное уравнением (3.4) является непериодическим. Промежуток времени между двумя последовательными прохождениями точки через начало координат называют условным полупериодом затухающих колебаний. Условный период Т и частота колебаний связаны зависимостью
- амплитуда, Н- частота, α- начальная фаза затухающих колебаний. Движение, представленное уравнением (3.4) является непериодическим. Промежуток времени между двумя последовательными прохождениями точки через начало координат называют условным полупериодом затухающих колебаний. Условный период Т и частота колебаний связаны зависимостью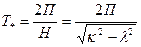 . (3.5)
. (3.5)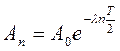 , (n=0,1,2,…)
, (n=0,1,2,…) называется декрементом, а величина
называется декрементом, а величина  - логарифмическим декрементом затухающих колебаний.
- логарифмическим декрементом затухающих колебаний.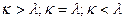 ?
? ) в амплитудной форме.
) в амплитудной форме.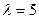 с -1.
с -1.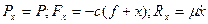 .
. . (3.6)
. (3.6)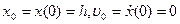 . (3.7)
. (3.7) , следовательно, движение представляет собой затухающие колебания. Поэтому общее решение уравнения (3.1) должно иметь вид (3.4).
, следовательно, движение представляет собой затухающие колебания. Поэтому общее решение уравнения (3.1) должно иметь вид (3.4).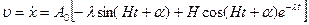 . (3.8)
. (3.8)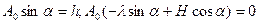 .
.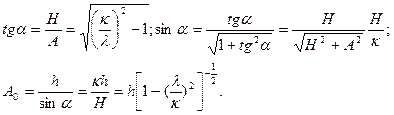
 (с -2);
(с -2); 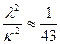 ;
; (с -1).
(с -1).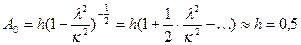 (см);
(см);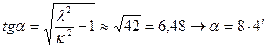 .
. , мы допускаем пренебрежимо малую ошибку. Поэтому искомый закон движения поршня (3.4) можно записать в следующем виде:
, мы допускаем пренебрежимо малую ошибку. Поэтому искомый закон движения поршня (3.4) можно записать в следующем виде: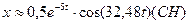 .
.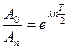 , то, логарифмируя, получаем
, то, логарифмируя, получаем  .
. .
. , имеем
, имеем .
. , можно управлять гашением колебаний, добиваясь практического приведения механической системы в равновесие в заданный промежуток времени или заданного рассеяния энергии колебаний.
, можно управлять гашением колебаний, добиваясь практического приведения механической системы в равновесие в заданный промежуток времени или заданного рассеяния энергии колебаний.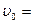 10 см/сек, направленная вверх.
10 см/сек, направленная вверх.


