Постановка второй основной задачи динамики
Рассмотрим материальную точку массой m. Дифференциальные уравнения точки в прямоугольных декартовых координатах имеют следующий вид:
Здесь X, Y, Z означают проекции равнодействующей системы сил, действующих на материальную точку. В дальнейшем будем предполагать, что эти проекции являются функциями семи переменных: времени t, координат x, y, z, точки и проекций ее скорости Вторая основная задача динамики ставится следующим образом. Даны: масса материальной точки, проекции действующей на нее силы как функции семи переменных t, x, y, z,
Требуется найти решение системы дифференциальных уравнений (1.1), удовлетворяющее условиям (1.2). Существование и единственность решения поставленной задачи гарантируется теоремой Коши, которая доказывается в подробных курсах дифференциальных уравнений. Искомыми решениями второй основной задачи динамики являются кинематические уравнения вида
Для решения второй основной задачи динамики применяются различные методы: аналитические (точные и приближенные), численные и качественные. Среди аналитических методов чаще всего используют метод разделения переменных и известные методы решения линейных дифференциальных уравнений с постоянными коэффициентами. Перед изучением раздела «Прямолинейные колебания» рекомендуется повторить соответствующие разделы из курса высшей математики.
План решения второй основной задачи динамики точки При решении второй основной задачи динамики точки рекомендуем руководствоваться следующим планом. 1. Выбрать и начертить систему координат (если она не задана в условии задачи). 2. Изобразить на чертеже точку текущий (произвольный) момент времени и все силы, действующие на нее в процессе движения. 3. Записать математические выражения действующих на точку сил и найти их проекции на координатные оси. 4. Составить дифференциальные уравнения движения. 5. Показать на чертеже положение точки и направление скорости в начальный момент времени; записать начальные условия. 6. Проинтегрировать дифференциальные уравнения движения и определить постоянные интегрирования из начальных условий. 7. Ответить на другие вопросы задачи. 8. Произвести исследование и проверку правильности решения задачи.
При разборе типовых задач рекомендуем проследить как реализуется этот план и самостоятельно выделить основные этапы решения. Отметим, что основной целью решения рассматриваемой задачи является выяснение физических свойств изучаемого движения. Математический аппарат, применяемый при решении задачи, является лишь средством для достижения этой цели. Поэтому последний пункт приведенного выше плана играет доминирующую роль. Постановка второй основной задачи динамики связана с выполнением первых пяти пунктов упомянутого плана. Она также играет основную роль в решении задачи. Целесообразно далее рассмотреть несколько примеров на постановку и решение второй основной задачи динамики для колебательных движений точки.
|

 . (1.1)
. (1.1)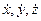 . Кроме того, потребуем, чтобы X, Y, Z имели непрерывные производные по каждой из указанных переменных.
. Кроме того, потребуем, чтобы X, Y, Z имели непрерывные производные по каждой из указанных переменных.
 (1.2)
(1.2)


