Вынужденные колебания точки
Используя прежнюю механическую модель (§2) и предполагая, что на груз в произвольном положении действуют линейная восстанавливающая сила F и вынуждающая сила
Полагая
Будем различать два случая: 1.
. Второе слагаемое в правой части (4.3) представляет вынужденные колебания. Амплитуда этих колебаний
Их частота
2.
Амплитуда вынужденных колебаний возрастает пропорционально времени t. Сдвиг фазы В случае произвольной вынуждающей силы F (t) дифференциальное уравнение вынужденных колебаний имеет вид
С помощью метода вариации произвольных постоянных можно представить общее решение уравнения (6.8), удовлетворяющее начальным условиям (4.2), в следующем виде:
В частности, если сила Ф(t) действует на материальную точку, которая в начальный момент (t=t0) находится в покое, то x0=0,
Решение (4.10) представляет собой вынужденное движение, порожденное силой Ф(t) группы слагаемых
В правой части (4.9) - это свободные колебания точки, вызванные возмущением ее состояния покоя, т.е. сообщением ей начального отклонения x0 начальной скорости Если на точку действуют линейная восстанавливающая сила F=cx, сила вязкого сопротивления
Ограничимся случаем затухающих колебаний. С помощью метода вариации произвольных постоянных можно представить решение уравнения (4.12), удовлетворяющее начальным условиям (4.2) в виде
В частности, если сила Ф(t) действует на материальную точку, которая в начальный момент находится в покое, то
Формула (4.14) представляет собой вынужденное движение точки, порожденное силой. Группа слагаемых
Вопросы для самоконтроля 1. Запишите дифференциальное уравнение движения точки под действием восстанавливающей и возмущающей силы. 2. Какой вид имеет частное решение этого уравнения при 3. Зависят ли чисто вынужденные колебания от начальных условий? 4. Как выражается амплитуда чисто вынужденных колебаний при отсутствии сил сопротивления? Постройте график изменения этой амплитуды в зависимости от отношения 5. Запишите дифференциальное уравнение движения точки под действием восстанавливающей, возмущающей сил и силы сопротивления, пропорциональной первой степени скорости? 6. В каком виде ищется частное решение этого уравнения? Как выражается амплитуда вынужденных колебаний в этом случае? Начертите график изменения амплитуды в зависимости от отношения 7. Запишите формулу, определяющую сдвиг фазы вынужденных колебаний. Постройте график изменения сдвига фазы в зависимости от отношения 8. В чем заключается явление резонанса? Как влияют силы сопротивления на это явление? 9. Выведите формулы (4.9) и (4.13) с помощью метода вариации произвольных постоянных. 10. Рассмотрите случай гармонической возмущающей силы
Пример
При вертикальных колебаниях станины вибрографа магнит совершает вертикальные колебания. Абсолютное движение магнита складывается из переносного движения (по отношению к станине). Будем рассматривать магнит как материальную точку. Поместим начало координат О в положении покоя магнита, соответствующем y=0. Отметим еще четыре точки: верхний конец А и нижний конец О1 недеформированной пружины при y=0; положение этих точек в текущий момент времени обозначим буквами А и М соответственно. В текущем положении на магнит действуют: сила тяжести Р и упругая реакция пружины F=c(ƒ+x+y). Дифференциальное уравнение абсолютного движения магнита примет вид
Вводя обозначение
Дифференциальное уравнение (4.16) имеет вид (4.2). Его частное решение при
Описывает вынужденные колебания магнита относительно неподвижных осей (абсолютное движение). Движение магнита относительно станины вибрографа описывается уравнением
Из (4.17) видно, что частота и фаза колебаний записываются точно, а амплитуда колебаний - с искажением. Так как
то при
Упражнения 1. Решите задачи: № 32.78; 32.84; 32.80; 32.86 из (7). 2. Найти движение материальной точки, пренебрегая силами сопротивления, при нулевых начальных условиях
Редактор Н.Е. Гладких Темплан 2007г., поз.156. Подписано в печать 22.05.07. Формат 60х84 1/16. Ризограф. Бумага писчая. Уч.-изд.л.1,2. Тираж 50 экз. Заказ 412. Редакционно-издательский центр РГСУ. 344022, Ростов н/Д, ул.Социалистическая, 162.
|

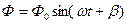 , получаем следующее дифференциальное уравнение движения
, получаем следующее дифференциальное уравнение движения . (4.1)
. (4.1)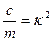 , запишем (6.1) в стандартной форме
, запишем (6.1) в стандартной форме . (4.2)
. (4.2) и
и 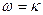 .
. (4.3)
(4.3) . (4.4)
. (4.4) совпадает с частотой вынуждающей силы,
совпадает с частотой вынуждающей силы, 
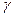 - сдвиг фазы
- сдвиг фазы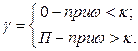
 .
. (4.7)
(4.7) .
. . (4.8)
. (4.8) . (4.9)
. (4.9)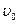 и (4.9) принимает вид
и (4.9) принимает вид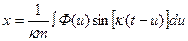 . (4.10)
. (4.10) . (4.11)
. (4.11)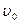 .
.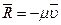 и произвольная возмущающая сила Ф(t), то дифференциальное уравнение вынужденного движения точки имеет вид
и произвольная возмущающая сила Ф(t), то дифференциальное уравнение вынужденного движения точки имеет вид . (4.12)
. (4.12)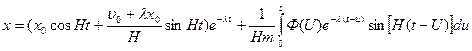 . (4.13)
. (4.13)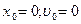 и (4.13) принимает вид
и (4.13) принимает вид .
.  представляет собой свободные затухающие колебания точки, вызванные возмущением ее состояния покоя, т.е. сообщением ей начального отклонения x0 и начальной скорости
представляет собой свободные затухающие колебания точки, вызванные возмущением ее состояния покоя, т.е. сообщением ей начального отклонения x0 и начальной скорости 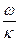 .
.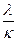 и сравните его с соответствующим графиком при
и сравните его с соответствующим графиком при  .
.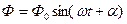 . найдите движение точки с помощью формул (4.9) и (4.13).
. найдите движение точки с помощью формул (4.9) и (4.13). .
. и принимая во внимание, что P=cƒ, получаем
и принимая во внимание, что P=cƒ, получаем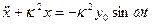 . (4.16)
. (4.16)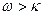
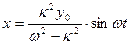 .
. . (4.17)
. (4.17)
 искажение амплитуды становится весьма малым. Распоряжаясь параметрами С и m, можно поэтому добиться выполнения условия
искажение амплитуды становится весьма малым. Распоряжаясь параметрами С и m, можно поэтому добиться выполнения условия 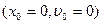 , если вынуждающая сила Ф(t) имеет синусоидальный вид.
, если вынуждающая сила Ф(t) имеет синусоидальный вид.


