1. Придание наглядности комплексному чертежу. На комплексном чертеже прямую, пересекающуюся с плоскостью, изображают: сплошной линией - проекции видимой части прямой, расположенной перед или над плоскостью: и штриховой — невидимой части, расположенной за или под плоскостью.
Границей видимой части в каждом случае служит проекция точки пересечения прямой с плоскостью.
Определить видимую часть прямой в каждой проекции следует отдельно.
2. Понятие видимости точек на комплексном чертеже. На (фиг.255,а) на горизонтально-проектирующей прямой лежат точки А, В и С. Наблюдатель, смотрящий «сверху» (показано стрелкой), первой увидит точку А и не может видеть остальные точки В и С, так как они закрыты точкой А.
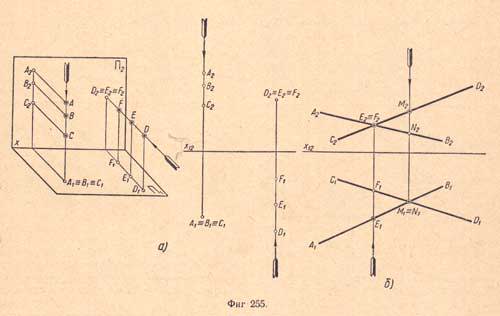
Отсюда видимой точкой из трех будет точка А, как наиболее удаленная от плоскости П1 т.е. имеющая наибольшую высоту; она определяется на комплексном чертеже по наибольшему расстоянию фронтальной проекции от оси х12.
То же можно сказать и о точке D. Наблюдатель, смотрящий «спереди» (показано стрелкой), первой увидит точку D и не может видеть точек Е и F, так как они закрыты точкой D; следовательно, из трех данных точек будет видимой только точка D; она наиболее удалена от плоскости П2, так как имеет наибольшую глубину. На комплексном чертеже она определяется по наибольшему расстоянию горизонтальной проекции от оси x12
Определив понятие видимости точки, рассмотрим это в применении на двух скрещивающихся прямых (фиг.255,б).
Задача состоит в том, чтобы установить, какая из точек является видимой и какая невидимой.
Рассматривая на комплексном чертеже одноименные горизонтальные проекции E1 и F1 устанавливаем, что точка Е1 имеет глубину большую, чем точка F1 т. е. точка Е удалена от плоскости П2 дальше, чем точка F. Следовательно, точка Е при виде спереди (в плоскости П2) является видимой. По одноименным фронтальным проекциям прямых видно, что прямая АВ в точке Е расположена перед прямой CD.
По расположению на фронтальных проекциях точек М2 и N2 видно, что высота точки М2 больше высоты точки N2, т.е. точка М находится дальше от плоскости П1 чем точка N. Следовательно, точка М при виде сверху (в плоскости П1) является видимой. Рассматривая одноименные горизонтальные проекции прямых, заключаем, что прямая CD в точке Мнаходится над прямой АВ.
Разберем, как на комплексном чертеже пересечения прямой с треугольником следует определять видимые участки прямых (фиг.256).
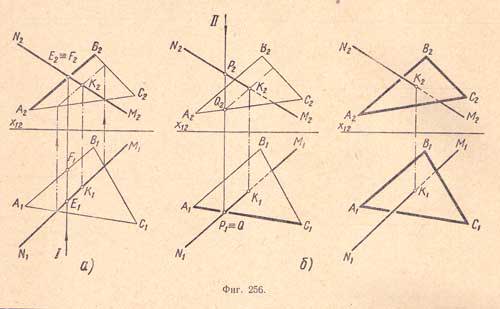
Точка К пересечения данной прямой с треугольником найдена согласно указаниям, данным в описании к (фиг.251).
а) Точка Е принадлежит отрезку NK; точка F - стороне АВ треугольник. Надо определить, какой из отрезков, NK или AB, находится перед другим.
Возьмем направление лучей зрения по стрелке 1 (фиг.256,a), горизонтальная проекция - точка Е1 - находится дальше от оси х12, чем проекция точки F1отсюда следует, что точка Е является видимой. Следовательно, на виде спереди отрезок, проходящий через точку Е, будет находиться перед стороной АВ треугольника AВС.
б) Точка Р принадлежит отрезку NК; точка Q - стороне АС треугольника. Надо определить, какой из отрезков, NK или АС, находится один над другим. Возьмем направление луча зрения по стрелке 11 (фиг.256,б); фронтальная проекция - точка Р2 - находится дальше от оси х12, чем проекция точки Q2, отсюда точка Р2 является видимой и, следовательно, отрезок, проведенный через эту точку, будет находиться над стороной АСтреугольника ABC.






