Общие сведения. Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Наиболее простыми являются гармонические колебания, при которых какая-либо физическая величина, характеризующая колебание, изменяется со временем по закону синуса или косинуса. Примером может служить колебание маленького шарика, подвешенного на длинной нити. Если пренебречь силой трения, то величина смещения шарика из положения равновесия изменяется по закону
или (1)
Колебательные процессы будут незатухающими, если они совершаются под действием только упругой или квазиупругой силы. В любой реальной колебательной системе всегда существует сила сопротивления, поэтому все реальные колебательные процессы затухающие. Отклоним шарик, подвешенный на нити, из положения равновесия (рис. 1). Применив к нему второй закон Ньютона, имеем
или
где m - масса шарика, a - ускорение, При малых колебаниях F 1 = - kx, а F C = - rυ;, где x - смещение, r - коэффициент сопротивления. Введем следующие обозначения:
Тогда уравнение (2) примет вид:
Уравнение (4) называется уравнением динамики затухающих гармонических колебаний, где b - коэффициент затухания. Если затухание невелико (b <;w0), то решением уравнения (4) является выражение
Здесь e - основание натурального логарифма.
Следует отметить, что затухающие колебания не являются периодическими, т.к. через одинаковые промежутки времени состояние наблюдаемой системы в точности не повторяется. Однако эти колебания условно характеризуют частотой и периодом в том смысле, что колеблющаяся система проходит положение равновесия в одном и том же направлении через равные промежутки времени. Частоту затухающих колебаний определим по формуле
где Изучать затухающие колебания можно только при b<w0. При b>w0 колебания становятся апериодическими. Отметим, что в данной работе период затухающих колебаний незначительно отличается от периода свободных колебаний, т.е. b<<w0. Для характеристики быстроты затухания колебаний вводят величину, называемую логарифмическим декрементом затухания d, который числено равен натуральному логарифму отношения двух амплитудных значений изменяющийся величины, отстоящих по времени одно от другого на период:
Выясним физический смысл этой характеристики. Пусть за t секунд амплитуда колебаний уменьшится в e раз. Тогда из (6), зная, что lne = 1, имеем
bt = 1. (7)
Тогда из (6) с учетом (7) получим
где Ne - число колебаний, совершенных системой за время t. Из выражения (8) следует, что d есть величина, обратная числу колебаний Ne, совершенных системой за время, в течение которого амплитуда уменьшится в e раз. Время t называется временем релаксации. Скорость затухания колебаний характеризуется также физической величиной, называемой добротностью Q, которая может быть определена как отношение максимального значения квазиупругой силы к максимальной силе сопротивления:
Максимальное значение квазиупругой силы F 1max = kA, где Максимальное значение силы сопротивления пропорционально максимальной скорости F cmax = ru max, где umax = A w0 (см. (3)). Тогда
Сделав замену ω0 = 2π/ T и учитывая (6), окончательно получим
Из выражения (9) следует, что добротность колебательной системы тем выше, чем большее число колебаний успевает совершиться, прежде чем амплитуда уменьшится в e раз. При слабом затухании добротность системы пропорциональна отношению энергии W, запасенной в системе, к убыли этой энергии Δ W за один период:
В этом заключается энергетический смысл добротности колебательной системы.
|

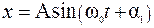 ,
,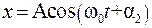 ,
, где A - амплитуда колебания; w0 - циклическая частота; a1, a2 - начальные фазы колебания.
где A - амплитуда колебания; w0 - циклическая частота; a1, a2 - начальные фазы колебания.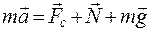 , (2)
, (2)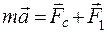 ,
,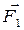 - квазиупругая сила,
- квазиупругая сила, 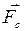 - сила сопротивления.
- сила сопротивления.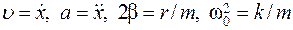 . (3)
. (3)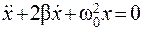 . (4)
. (4)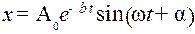 . (5)
. (5) Графически это решение представлено на рис. 2. Амплитуда затухающих колебаний изменяется по экспоненциальному закону.
Графически это решение представлено на рис. 2. Амплитуда затухающих колебаний изменяется по экспоненциальному закону.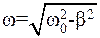 ,
,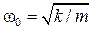 - частота собственных колебаний системы при отсутствии силы сопротивления.
- частота собственных колебаний системы при отсутствии силы сопротивления.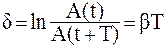 . (6)
. (6) , (8)
, (8)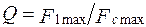 .
.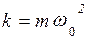 , (см. (3)).
, (см. (3)).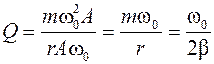 .
.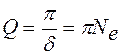 . (9)
. (9) . 10
. 10


