Выявление нормального распределения

Обычно в статистике предполагают, что распределение данных приблизительно соответствует нормальному. Это объясняется тем, что многие стандартные методы статистического анализа, например, вычисление доверительных интервалов или проверка статистических гипотез, требуют нормального распределения данных (хотя бы приблизительно). Зная свойства нормального распределения и изучив внимательно гистограмму, важно определить, являются ли данные нормально распределенными.

Теоретически нормальное распределение представляет собой гладкую гистограмму в форме колокола без случайных отклонений. Кривая нормального распределения задается функцией плотности распределения:

,

где a и σ;² – параметры распределения: a – математическое ожидание; σ;² – дисперсия данной случайной величины. Для идеального набора нормально распределенных данных такая кривая имеет следующий вид:

Как видим, большинство чисел сконцентрировано в средней части диапазона значений (центр колокола a), а оставшиеся значения с затуханием симметрично располагаются по обе стороны от вершины колокола. Величина σ; характеризует ширину (масштаб) колокола.

Фактически существует много кривых нормального распределения, форма которых напоминает симметричный колокол. Эти кривые отличаются друг от друга расположением центра и масштабом σ;. Ниже показаны кривые нормального распределения, построенные в разных масштабах.

Поскольку реальные наборы нормально распределенных данных носят случайный характер, то они не имеют идеальную степень гладкости гистограмм и содержат некоторые случайные отклонения от теоретической кривой.

Задание 2.

Построить гистограммы для двух различных выборок объемом по 100 значений каждая из нормально распределенного набора данных.

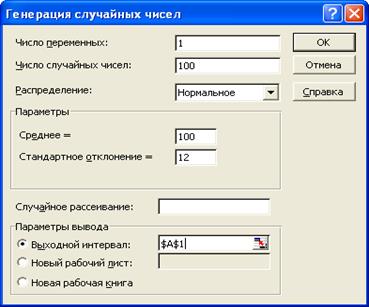
Для получения выборки из нормально распределенного набора данных используйте статистический пакет Анализ данных. Выполните следующие действия.

1. Откройте файл Гистограммы.xls и выделите Лист2.

2. Выберите из меню команду: Сервис®Анализ данных®Генерация случайных чисел. Щелкните на кнопке OK.

3. В появившемся диалоговом окне установите параметры, как показано ниже. Щелкните на кнопке OK.

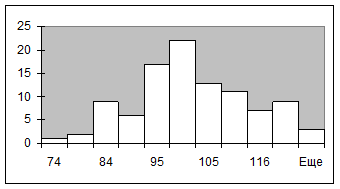
4. Для полученной выборки на том же Листе2 постройте гистограмму, разместите ее вместе с таблицей распределения частот в диапазоне G1:N16 и приведите к виду, указанному ниже.

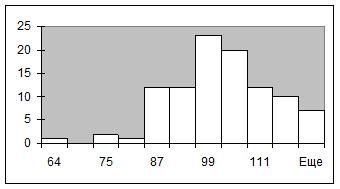
5. Получите вторую выборку из нормально распределенных данных с теми же параметрами и разместите ее на Листе2 в диапазоне B1:B100.

6. Для второй выборки постройте гистограмму, расположите ее вместе с таблицей распределения частот в диапазоне G21:N36 и приведите к виду, указанному ниже. Щелкните на кнопке Сохранить.

Сравнение этих двух гистограмм показывает, насколько случайной может быть форма распределения при ограниченном объеме выборки. Значительное уменьшение объема выборки приводит к увеличению случайности и может быть недостаточно для представления полной картины распределения.

Задание 3.

Построить гистограммы для двух различных выборок объемом по 15 значений каждая из нормально распределенного набора данных.

В файле Гистограммы.xls выделите Лист3.

Используя статистический пакет Анализ данных, получите две выборки объемом по 15 значений каждая из нормально распределенных данных с параметрами, указанными в Задании 2. Постройте гистограммы и сравните форму распределения. Щелкните на кнопке Сохранить.