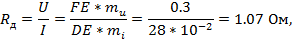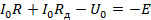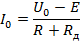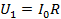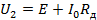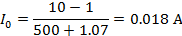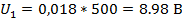Часть 2. Нелинейные электрические цепи.

 

Задание:

1. Изобразить электрическую схему нелинейной цепи, используя графическое обозначение конкретного нелинейного элемента (стабилитрона, диода, и т.п.) в соответствии с вариантом задания.

2. Построить в масштабе ампер–вольтные характеристики I(U) нелинейного элемента и резистора.

3. Определить ток I₀ в цепи и напряжения U₁ и U₂ на элементах цепи:

а) методом построения результирующей характеристики цепи;

б) методом построения опрокинутой характеристики.

4. Рассчитать заданную электрическую цепь методом линеаризации ампер – вольтной характеристики нелинейного элемента:

a) найти параметры линеаризации на рабочем участке характеристики (в окрестности рабочей точки, указанной в табл. 4);

b) составить схему замещения линеаризованной электрической цепи, используя найденные параметры Е, R_д линеаризации нелинейного элемента;

c) воспользовавшись схемой замещения, записать выражения для тока в цепи I₀ и напряжений U₁ и U₂ на элементах цепи;

d) найти конкретные значения величин I₀, U₁ и U₂.

Исходные данные:

Параметры нелинейной цепи

Номера личных в-тов	Название нелин. элемента НЭ	Номер хар-ки НЭ	Напряжение U0,В	Сопротивление R,Ом	Координаты точки на линеаризуемом участке НЭ
	Туннельный диод				U=1,3 В

 

Характеристика туннельного диода

 

U, В		0,1	0,2	0,5	1,0	1,2	1,5	Номер характеристики
I, мА

 

Электрическая схема нелинейной цепи:

Строим характеристики I(U) нелинейного элемента и резистора.

Характеристика резистора строится по уравнению I=U/R. Задаемся U=10B и получаем I= 10/500=20мА.

Строим результирующую характеристику по II закону Кирхгофа U=U₁+U₂. Задаемся несколькими значениями тока, для каждого по графикам определяем U₁ и U₂, складываем их, а полученные точки соединяем плавной кривой. По напряжению U₀ на результирующей характеристике определяем I₀. По току I₀ на характеристиках резистора и нелинейного элемента определяем U₁, U₂.

Строим опрокинутую характеристику резистора. Для этого определяем положение точек M и N

I_M=0, U_M=U₀=10B

U_N=0, I_N=U₀/R=20мА

Строим точки M и N и соединяем их прямой линией. В точке пересечения опрокинутой характеристики и ВАХ нелинейного элемента получаем ток I₀, U₂, U₁.

Проводим касательную к графику нелинейного элемента в точке с I=10 мА. Получаем прямую DF. В точке F определяем величину ЭДС схемы замещения (E=1B). Из треугольника DEF получаем

где m_u и m_i – масштабы по осям координат.

 

Схема замещения:

 

По второму закону Кирхгофа:

Отсюда

Для R:

Для R_д:

Подставляем числовые значения: