Поверхности.
1. 2. 3. Однополостный гиперболоид: 4. Двуполостный гиперболоид: 5. Эллиптический параболоид: 6. Гиперболический параболоид: 7. Цилиндры имеют те же уравнения, что и кривые второго порядка, но рассматриваются в пространстве: а). эллиптический
б). гиперболический
в). параболический
Образующие || оси OZ, а направляющий является эллипс, гипербола, парабола. 8. Конус второго порядка:
Исследование функции y=f(x). Если
Если
Вертикальная асимптота x=a, если Горизонтальная асимптота y=b, если Наклонная асимптота y=Kx+b, если K=
Точки разрыва функции могут быть в точках где функция не определена или при переходе через которые меняется формула для функции. Например, в точках, где знаменатель дроби = 0.
|
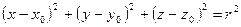- уравнение сферы радиуса r с центром в точке С (
).
- уравнение эллипсоида с полуосями a, b, c с центром в точке С 
.
.
.
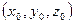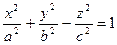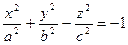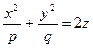(p>0, q>0).
(p>0, q>0).
.
.
или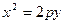 
с вершиной в начале координат, осью которого служит ось OZ.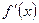
>0, то функция 
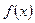возрастает,
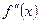<0, то график выпуклый (выпуклость вверх),
.
.
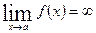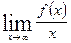, b=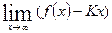 
.
