Рекомендации по обработке экспериментальных данных. Экспериментальные данные используются для расчёта среднего значения коэффициента теплопередачи за период охлаждения и для расчёта теоретического времени
Экспериментальные данные используются для расчёта среднего значения коэффициента теплопередачи за период охлаждения и для расчёта теоретического времени охлаждения жидкости при нестационарном теплообмене.
1. Расчёт коэффициента теплопередачи рекомендуется выполнить по уравнению (2.3.2) аддитивности термических сопротивлений при переносе теплоты через цилиндрическую незагрязненную стенку, для чего необходимо рассчитать коэффициенты теплоотдачи aвн и aн. 1.1. Расчёт коэффициента теплоотдачи от охлаждаемой воды к поверхности теплообменной трубы (a1 = aн) рекомендуется выполнять в следующем порядке:
а) определить физические свойства охлаждаемой воды при температуре, средней за период эксперимента, и, к тому же, средней вдоль поверхности теплообмена. Если найденное при выполнении работы 1.8 число ячеек идеального перемешивания п ≤ 2, то перемешивание жидкости в ёмкости с работающей мешалкой близко к идеальному. Принимая идеальное перемешивание охлаждаемой жидкости, то есть, полагая, что её температура не зависит от пространственной координаты, а зависит только от времени [ T 1= f (t)], средняя за период эксперимента температура может быть определена по соотношению:
б) определить критерий Нуссельта (Nu1), используя критериальное уравнение:
где
Определяющий линейный размер в критериях подобия уравнения (2.6.4) есть диаметр мешалки – d м. Поскольку температуры теплообменных поверхностей в данном аппарате не измеряются, рекомендуется сделать допущение: (m/mст)0,25» 1.
в) рассчитать коэффициент теплоотдачи:
1.2. Расчёт коэффициента теплоотдачи от поверхности теплообменной трубы к охлаждающей воде (a2 = aвн) рекомендуется выполнять в следующем порядке:
а) определить физические свойства охлаждающей воды при температуре, средней за период эксперимента, и, к тому же, средней вдоль поверхности теплообмена. Температура охлаждающей воды, подаваемой в змеевик, в общем случае изменяется во времени как в точке входа в змеевик, так и в точке выхода из него. Средняя за период эксперимента температура воды на входе в змеевик может быть определена по соотношению:
Средняя за период эксперимента температура воды на выходе из змеевика:
Осреднение температуры по длине змеевика может быть выполнено по упрощённому соотношению:
б) рассчитать среднюю скорость воды в трубке змеевика и критерий Рейнольдса (Re2);
в) рассчитать число Нуссельта (Nu2), используя одно из приведённых ниже критериальных уравнений: ▫ при 13,5·(d вн/ D вит) -0,5 < Re < 18500·(d вн/ D вит)0,28, что соответствует ламинарному течению с вторичной циркуляцией жидкости,
▫ при Re > 18500·(d вн/ D вит)0,28, что соответствует турбулентному течению с вторичной циркуляцией жидкости,
Поскольку температуры теплообменных поверхностей в данном аппарате не измеряются, рекомендуется сделать следующее допущение:
г) рассчитать коэффициент теплоотдачи:
1.3. Рассчитать коэффициент теплопередачи по (2.3.2).
2. Вычисленное значение коэффициента теплопередачи использовать для расчета теоретического времени охлаждения по формуле (2.6.1).
Сделать заключение о применимости теоретического расчёта к прогнозированию времени охлаждения жидкости в аппарате с мешалкой и змеевиком при заданном коэффициенте теплопередачи и при заданных начальной и конечной температурах.
|

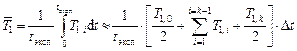 ;
;
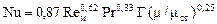 ,
,
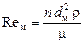 – критерий Рейнольдса при перемешивании;
– критерий Рейнольдса при перемешивании;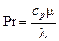 – критерий Прандтля;
– критерий Прандтля;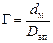 – симплекс геометрического подобия.
– симплекс геометрического подобия. .
.
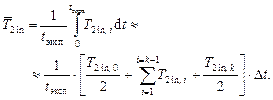
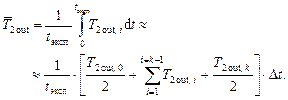
 ;
;
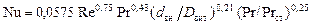 ;
;

 .
.
 ;
;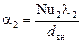 .
.



