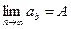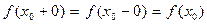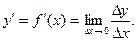Словарь терминов. Тема 1. Элементы теории множеств
Тема 1. Элементы теории множеств q Множество - совокупность, набор каких-либо предметов (объектов). q Элементы множества - предметы, составляющие множество. q Пустое множество - множество, не содержащее ни одного элемента. q Равные множества - если AÌB и одновременно BÌA, то A = B. q Объединение множеств - такое множество AÈB, которое состоит из всех элементов, принадлежащих множеству A или B. q Пересечение множеств - такое множество AÇB, которое состоит из элементов, принадлежащих множеству A и множеству B одновременно. q Разность множеств - множество A\B, состоящее из всех элементов множества A, не входящих во множество B. q Открытый интервал (числовой промежуток) - множество всех чисел x, которые удовлетворяют неравенствам a < x < b. q Замкнутый интервал (числовой отрезок) - множество всех чисел x, которые удовлетворяют неравенствам a £ x £ b. q Окрестность точки - любой открытый интервал, содержащий эту точку. q Отображение множества A во множество B - такое соответствие, при котором каждому элементу aÎA некоторым способом поставлен в соответствие элемент bÎB. q Отображение множества A на множество B - такое соответствие, при котором каждому элементу aÎA некоторым способом поставлен в соответствие элемент bÎB, и при этом каждый элемент множества B соответствует какому-либо элементу множества A. q Взаимно- однозначное соответствие (взаимно-однозначное отображение) множеств - такое соответствие, при котором каждому элементу aÎA некоторым способом поставлен в соответствие элемент bÎB, и при этом каждый элемент bÎB соответствует одному и только одному элементу aÎA. q Эквивалентные множества - множества, между которыми можно установить взаимно- однозначное соответствие. q Счетное множество - бесконечное множество, эквивалентное множеству натуральных чисел. Тема 2. Прогрессии. Проценты q Арифметическая прогрессия - числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d (d - разность прогрессии). q Геометрическая прогрессия - последовательность на равных нулю чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число q (q - знаменатель прогрессии). q Бесконечная убывающая геометрическая прогрессия - геометрическая прогрессия, у которой модуль знаменателя меньше единицы. q Процент - сотая часть числа. q Формула простых процентов - S = P×(1+n×i), где P - первоначальный вклад, i - процентная ставка, S - суммарная величина вклада в конце n-го периода, величина (1+n×i) - множитель наращения простых процентов. q Формула сложных процентов - S =P×(1+i)n, где P - первоначальный вклад, i - процентная ставка, S - суммарная величина вклада в конце n-го периода, величина (1+×i)n - множитель наращения сложных процентов. Тема 3. Числовые функции и графики q Числовая функция – отображение числового множества D (область определения функции) в числовое множество Ф (область значений функции). q График функции - множество точек на плоскости, у которых абсциссы являются допустимыми значениями аргумента, а ординаты - соответствующими значениями функции. q Область определения функции – множество значений независимой переменной, при которой функция y = f(x) имеет смысл. q Область значений функции – множество значений, которые принимает функция на всей области своего определения q Основные элементарные функции - степенная, показательная, логарифмическая, тригонометрическая, обратные тригонометрические. q Сложная функция - функция, получающаяся из элементарных функций с помощью операции «взятия функции от функции». q Четная функция - функция, для которой при любом xÎD выполняется равенство f(-x) = f(x). q Нечетная функция - функция, для которой при любом xÎD выполняется равенство f(-x) = -f(x). q Возрастающая в интервале функция - такая функция, для которой при любых x1,x2Î(a,b) таких, что x1 < x2, выполняется неравенство f(x1) < f(x2). q Убывающая в интервале функция - такая функция, для которой при любых x1,x2Î(a,b) таких, что x1 < x2, выполняется неравенство f(x1) > f(x2). q Четная функция - функция f, у которой для всех x из ее области определения справедливо равенство f(-x) = f(x). q Нечетная функция - функция f, у которой для всех x из ее области определения справедливо равенство f(-x) = -f(x). Тема 4. Начала математического анализа q
Предел последовательности {an} - число A, к которому можно приблизиться с любой степенью точности при стремлении номера члена последовательности к бесконечности q
Предел функции y = f(x) при стремлении аргумента x к фиксированному значению x0 - число A, к которому значение функции y может приблизиться с любой наперед заданной точностью e: q
Два замечательных предела -
q
Функция y = f(x) непрерывна в точке x =x0 - если ее предел в точке x0 равен значению функции в этой точке
т.е. существует значение функции в точке x0, y =f(x0), ее предел справа равен пределу слева при x®x0 и равен значению функции в этой точке:
Тема 5. Понятие производной. Применение производной при исследовании функций q
Производная функции в точке x0 - предел отношения приращения функции Dy к приращению аргумента Dx при стремлении Dx к нулю: q Дифференциал функции y = f(x) в точке x0 - произведение производной функции f¢(x0) на приращение аргумента Dx, т.е. dy = f¢(x0)×Dx, если x - независимая переменная, то dy = f¢(x0)×dx. q Геометрический смысл дифференциала - дифференциал функции y = f(x) в точке x0 равен приращению ординаты касательной при x®x0, первое линейное приращение. q Точка максимума (минимума) функции y = f(x) - точка x0, для которой существует такая окрестность точки x0, что для всех точек x ¹ x0 принадлежащих этой окрестности, выполняется неравенство f(x0) > f(x) (f(x0) < f(x)). q Асимптота к графику функции y = f(x) -прямая, к которой приближается точка M(x,y), лежащая на графике, при неограниченном удалении ее от начала координат; асимптоты бывают наклонные y = kx+b или вертикальные x = a. Тема 6. Неопределенный интеграл q Первообразная функция от заданной функции f(x) - функция F(x), производная которой равна f(x), или дифференциал которой равен f(x)dx, т.е. F¢(x) = f(x) dF(x) = f(x)dx. q Неопределенный интеграл функции f(x) - совокупность всех первообразных, т.е. выражение вида F(x) + C, где F(x) - первообразная функции f(x), C - постоянная величина: òf(x)dx = F(x) + C. Тема 7. Определенный интеграл q Определенный интеграл функции f(x) - число, равное площади криволинейной трапеции, ограниченной непрерывной кривой y = f(x) (f(x) ³ 0 на отрезке [a,b]), осью OX и прямыми x = a, x = b. q
Основные свойства определенного интеграла: если интервал интегрирования [a,b] разбит на части [a,c] и [c,b]. q Несобственный интеграл по бесконечному промежутку интегрирования - определенный интеграл, у которого хотя бы один из пределов бесконечен. q
Несобственный интеграл сходится, если существует конечный предел:
|