Построение симплекс-таблиц
Переход от одного базисного решения к другому соответствует переходу от одной симплекс-таблицы к другой. 1. Заполнить таблицу данными задачи 2. Рассмотреть все коэффициенты 3. Пусть среди коэффициентов при x в целевой функции есть положительные. Выбираем любой из них. Смотрим на соответствующий ему столбец. Если среди коэффициентов a в этом столбце все неположительные, то оптимального решения нет 4. Пусть в этом столбце имеются коэффициенты больше 0. Для каждого из них находим отношение
Строка с номером i – разрешающая, столбец j – разрешающий, элемент aij – разрешающий элемент 5. В нижнюю половину разрешающей клетки пишем 6. Каждый элемент разрешающей строки (кроме aij) умножаем на 7. Каждый эл-т разрешающего столбца (кроме aij) умножаем на 8. Выделяем в строке верхние половины клеток а в столбце – нижние. 9. Для всех клеток не принадлежащих раз-м столбцу и строке в нижнюю половину запишем произведение выделенных эд-в в данной строке и столбце. 10. Составим новую таблицу, в которой поменяем местами xi и xj 11. В верхние половины клеток бывшей разре-й строки и столбца запишем нижние элементы соотв. клеток старой таблицы. Во все остальные клетки запишем сумму верхних и нижних клеток. 12. переход на 2
|
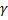при переменных x в целевой функции, если они все отрицательные, значит решение оптимально
и среди них выбираем минимальное
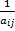
и пишем в нижнюю половину клетки
