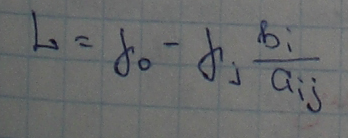Основные положения симплекс-методаЕсли число нулевых свободных переменных равно n-m, то это решение – вершина симплекса. Значение целевой функции 1. Пусть в решении (1) все Значения свободных переменных нельзя уменьшить, так как тогда они станут меньше 0 (они уже все равны 0 и меньше 0 быть не могут). Но и при увеличении любого из x значение функции L также будет увеличиваться. Значит данное решение (со всеми неположительными гамма) оптимально. 2. Существует a.
В этом случае нет оптимального решения b.
Тогда при увеличении
Элемент
Такое увеличение привело к тому, что переменная xi уменьшилась до 0 и стала свободной, а переменная xj стала базисной. Значение целевой функции уменьшилось до
|
.
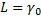
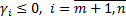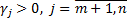
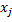некоторые базисные x будут уменьшаться.
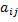удовлетворяющий условию (*) называют разрешающим, строку и столбец с ним – разрешающей строкой и столбцом.
