Примеры решения задач
ЗАДАЧА 1. Определить амплитуду AР вынужденных колебаний при резонансе, если при очень малой (по сравнению с собственной) частоте вынужденных колебаний она равна А 0 = 0,10 см, а логарифмический декремент затухания Q =0,010.
АНАЛИЗ. В задаче рассматривается резонанс вынужденных колебаний. РЕШЕНИЕ. Амплитуда вынужденных колебаний при резонансе (w=w Р) достигает максимального значения АР согласно формуле (1.4.5): Найдем значения величин f 0 и b. Учтем, что амплитуда вынужденных колебаний определяется по формуле (1.4.2) Из условия задачи следует, что w<<w0 при А = А 0, поэтому
Считая затухание b малым по сравнению с собственной частотой w0 осциллятора, получим: Найдем затухание b по известному значению логарифмического декремента затухания из соотношения (1.3.9) ОТВЕТ: АР = 0,31 см.
ЗАДАЧА 2. Определить жесткость пружин рессор вагона, масса которого с грузом 50 тонн, если при скорости u = 12 м/с вагон начинает сильно раскачиваться вследствие толчков на стыках. Длина рельса 12,8 м. Вагон имеет четыре рессоры.
АНАЛИЗ. В задаче рассматривается динамика вынужденных колебаний, вызванных ударами колес на стыках рельс. Раскачка вагона усиливается вследствие резонанса между собственными колебаниями вагона и вынуждающей силой. РЕШЕНИЕ. Пренебрегая затуханием, будем считать, что резонанс наступает, когда период Т 0 собственных колебаний вагона совпадает с периодом вынуждающей силы (Т = Т 0). Период вынуждающей силы равен времени прохождения вагоном длины рельса:
ОТВЕТ:
ЗАДАЧА 3. Тело массой т подвешено на пружине (ее жесткость
АНАЛИЗ. В задаче исследуется динамика вынужденных колебаний под действием упругой, вязкой и вынуждающей сил. Для получения уравнения колебаний следует воспользоваться вторым законом Ньютона.
РЕШЕНИЕ. На тело в жидкости (рис. 1.4.3) действуют: вынуждающая сила Запишем второй закон Ньютона:
Уравнение спроектируем на ось ОХ, учитывая, что
где V – объем тела. Продифференцируем (1.4.8) по времени и проведем преобразования:
Обозначив
Уравнение (1.4.9) линейное с постоянными коэффициентами, неоднородное. Его решение будем искать в виде
где u0 – амплитуда скорости, a – разность между фазами скорости и вынуждающей силы. Величины u0 и a найдем, подставив (1.4.10) в уравнение (1.4.9). Для этого найдем:
Представим тригонометрические функции от сложного аргумента
тогда
Уравнение (1.4.11) обратится в тождество, если в обеих частях равенства коэффициенты при
Из уравнения (1.4.12 а) получим:
Следовательно, разность фаз между скоростью и вынуждающей силой равна Проверим размерность: Чтобы найти амплитуду скорости, нужно возвести в квадрат и почленно сложить уравнения (1.4.12 а) и (1.4.12 б):
В результате получим: Найдем смещение х:
Учитывая (1.4.13), определим амплитуду смещения х 0:
Чтобы найти резонансную частоту w Р, продифференцируем выражение (1.4.14) по времени и приравняем к нулю. В результате получим:
После математических преобразований запишем: проверим размерность: Таким образом, скорость u и смещение х изменяются по гармоническому закону с частотой, равной частоте вынуждающей силы: Смещение х отстает по фазе от скорости u на ОТВЕТ:
ЗАДАЧА 4. Шарик массы m, подвешенный на невесомой пружине, может совершать вертикальные колебания с коэффициентом затухания b. Собственная частота колебаний w0. Под действием внешней вертикальной силы, меняющийся по закону:
АНАЛИЗ. Задача на динамику вынужденных колебаний. При решении необходимо воспользоваться вторым законом Ньютона. РЕШЕНИЕ. Под действием силы Сила Fх изменяется со временем. Найдем элементарную работу
где
Решением этого дифференциального уравнения будет гармоническая функция. Смещение х колеблющегося тела от положения равновесия вдоль оси ОХ определится как:
Величина амплитуды А 0 и сдвиг по фазе j между смещением и вынуждающей силой определяется при подстановке решения (1.4.17) в дифференциальное уравнение (1.4.16) как
Найдем скорость колеблющегося шарика, продифференцировав (1.4.17) по времени:
Элементарная работа, совершаемая вынуждающей силой, определяется по формуле (1.4.15), подстановкой значений u и F:
Элементарная работа знакопеременна; Мгновенная мощность определяется как Функцию
Интегрирование по переменной t в пределе от нуля до T соответствует интегрированию по переменой w t в пределе от 0 до 2p, поэтому
Подставим найденные значения интегралов и величину А 0из равенства (1.4.18). В результате средняя мощность силы F равна
т.е. Выразим sinj через величины w0, w,b, используя равенства (1.4.18) и (1.4.19). Учтем, что После математических преобразований запишем:
Отсюда получим Следовательно,
Проверим размерность: Мощность вынуждающей силы за период максимальна, если скорость колеблющегося шарика и вынуждающая сила изменяются со временем без сдвига по фазе, т. е. ОТВЕТ:
ЗАДАЧА 5. Найти период автоколебаний стержня массой m, лежащего на двух шероховатых валиках, вращающихся в противоположных направлениях с одинаковыми угловыми скоростями w. Расстояние между осями валиков
АНАЛИЗ. В задаче определяются условия возникновения автоколебаний стержня, расположенного на двух вращающихся валиках. При этом гармонические колебания происходят, если возвращающая сила в процессе колебания изменяется пропорционально смещению и направлена к положению равновесия. В задаче используются законы динамики для поступательного и вращательного движений.
РЕШЕНИЕ. Выберем систему координат, начало которой О совпадает с центром масс стержня, когда он находится посередине между осями валиков; ось ОХ направим вдоль стержня. В некоторый момент времени принятый за начальный, стержень выведен из этого положения, в результате чего его центр масс О отклонился на величину х по оси ОХ. На стержень действует сила тяжести
т. к. стержень вдоль оси ОY не перемещается. Стержень не вращается в вертикальной плоскости, поэтому сумма моментов сил относительно точки В равна нулю. На стержень относительно точки В действуют: момент силы тяжести Уравнение движения стержня вдоль оси ОХ согласно второму закону Ньютона имеет вид: Положительную величину
В результате получили уравнение колебаний ОТВЕТ: ЗАДАЧА 6. В колебательном контуре (рис. 1.4.6) емкость конденсатора изменяется скачком от значения С 1 до С 2 и обратно с периодом Т. Определить условия параметрического возбуждения колебаний, если добротность контура Q, а период собственных колебаний Т 0 = 2 Т.
АНАЛИЗ. В задаче определяются условия, необходимые для возбуждения в LCR – контуре параметрических колебаний, возникающих при изменении емкости С с периодом
РЕШЕНИЕ. Представим процесс, происходящий в колебательном контуре (рис. 1.4.6.) на фазовой плоскости осциллятора (рис. 1.4.7). Пусть в начальный момент времени, когда фаза колебаний равна нулю (точка А), емкость конденсатора мгновенно падает от значения С 1 до значения С 2. В этот момент частота колебаний осциллятора увеличивается до значения
При пересечении оси Q точка попадает в положение D, отстоящее от начала координат дальше, чем точка В контуре (рис. 1.4.6) есть потери энергии (на сопротивлении R выделяется джоулева теплота), которые должны приводить к скручиванию спирали на фазовой плосткости. Для возбуждения колебаний необходимо, чтобы эти потери энергии были меньше, чем энергия, подводимая к контуру извне при раздвижении пластин заряженного конденсатора (точка А). В этом случае для резкого уменьшения емкости конденсатора (
где С другой стороны в контуре за время Для возбуждения колебаний необходимо, чтобы увеличение энергии конденсатора Таким образом, условие параметрического возбуждения колебаний осциллятора с добротностью Q после подстановки значений При условии ОТВЕТ: Условие параметрического возбуждения колебаний осциллятора с добротностью Q имеет вид:
ЗАДАЧА 7. Найти закон изменения напряжения на обкладках конденсатора С в релаксационном генераторе с неоновой лампочкой Л. Схема генератора изображена на рис. 1.4.8.
АНАЛИЗ. Задача на электромагнитные колебания в релаксационном генераторе с неоновой лампочкой под действием внешней ЭДС. Лампочка Л представляет собой систему из двух электродов, промежуток между которыми заполнен неоном. Она является нелинейным элементом: если напряжение на конденсаторе меньше напряжения зажигания лампочки, (UC < U З) ее сопротивление бесконечно велико, ток через лампу не проходит; если напряжение UC больше напряжения зажигания лампы, ток проходит через нее, причем сопротивление неоновой лампы стремится к нулю. В генераторе возникают незатухающие колебания.
РЕШЕНИЕ. Уравнение зарядки конденсатора С можно получить, используя второе правило Кирхгофа:
Получили дифференциальное уравнение. Решим его методом разделения переменных:
Используем начальные условия: t =0, q 0 = 0 (конденсатор не заряжен, точка О на графике 1.4.9). Определив константу, найдем закон изменения заряда q на обкладках конденсатора при его зарядке со временем
Учитывая, что
Зависимость Когда разность потенциалов на обкладках конденсатора достигает напряжения зажигания (UC = U З), в неоновой лампе начинается ионизация газа. Плазма в разрядном промежутке становится хорошим проводником, сопротивление лампы RЛ ® 0. В результате начинается релаксационный процесс разрядки конденсатора C (участок графика ВС на рис. 1.4.9). Уравнение разрядки конденсатора найдем, используя второе правило Кирхгофа для контура АDEF Решая полученное дифференциальное уравнение методом разделения переменных, получим: За время горения лампы конденсатор разряжается от потенциала UЗ зажигания до потенциала U Г гашения по закону При Процесс периодический, но изменение напряжения на обкладках конденсатора не является косинусоидальной (синусоидальной) зависимостью. Это связано с тем, что в схеме рис. 1.4.8. имеется нелинейный элемент (неоновая лампочка). Процесс релаксационный, т. к. восстанавливается равновесное состояние. ОТВЕТ: ЗАДАЧА 8. В цепи, состоящей из последовательно соединенных резистора сопротивлением R =20 Ом, катушки индуктивностью L = 1,1 мГн и конденсатора емкостью C =0,10 мкФ действует синусоидальная ЭДС (рис 1.4.10). Определить частоту изменения ЭДС, при которой в цепи наступает резонанс. Найти действующие значения силы тока I и напряжений UR, UL, UC на всех элементах цепи при резонансе, если действующее значение ЭДС xД = 30 В.
АНАЛИЗ. Под действием переменной ЭДС в цепи, представляющей собой колебательный контур, установятся вынужденные электромагнитные колебания. При этом амплитудные значения тока I 0 и ЭДС x0 связаны по закону Ома (1.4.6).
РЕШЕНИЕ. Для действующих значений величин тока и напряжения
Максимальным будет значение тока IД для частоты
Следовательно, резонансная циклическая частота: Используя закон Ома, определим значение напряжения на каждом из элементов контура R, L, C для найденного значения IД:
При резонансе емкостное ОТВЕТ: ЗАДАЧА 9. Определить действующее значение силы тока на всех участках цепи, изображенной на рис. 1.4.12, если R = 1,0 Ом, L = 1,00 мГн,
АНАЛИЗ. В задаче рассматривается разветвленная цепь переменного тока: участок 1-2 является параллельным соединением двух ветвей, одна из которых содержит конденсатор С, другая – элементы R и L, соединенные между собой последовательно. Каждая из ветвей вместе с источником ЭДС образует колебательный (неполный) контур, поэтому силу тока в каждой ветви можно найти по формуле (1.4.23).
РЕШЕНИЕ. Для силы тока в ветви 1 С 2, где R = 0, L = 0, получим
Если бы переменные токи в обеих ветвях имели одинаковые фазы, то сила тока в неразветвленной части цепи согласно первому правилу Кирхгофа была бы равна сумме сил токов Таким образом, ток IC, текущий через емкость, опережает по фазе ЭДС на Токи IC и ОТВЕТ: ЗАДАЧА 10. Активное сопротивление R, индуктивность L и емкость С соединены параллельно и подключены к источнику переменного тока с ЭДС
АНАЛИЗ. В задаче рассматриваются вынужденные электромагнитные колебания в электрическом колебательном контуре с параллельно соединенными элементами LCR. Задача решается с использованием закона Фарадея и первого правила Кирхгофа. РЕШЕНИЕ. Из условия задачи (рис. 1.4.14) следует, что напряжение на всех элементах контура C, L, R одинаково и равно ЭДС, т. е.
Найдем токи в ветвях контура (IC, IL, IR), выразив их через соответствующее значение напряжения. Напряжение на обкладках конденсатора
Сравнивая выражения (1.4.24) и (1.4.25), получим, что ток через конденсатор опережает напряжение на конденсаторе UС на Напряжение на индуктивности связано с величиной тока
|

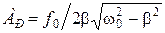 .
.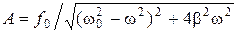 .
. , и
, и 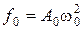 . Значение f 0 подставим в соотношение (1.4.5):
. Значение f 0 подставим в соотношение (1.4.5): .
. .
. , т. е.
, т. е.  . При затухании период Т затухающих колебаний, которые начались бы после прекращения действия вынуждающей силы, мало отличается от периода Т 0 собственных колебаний, т. е. Т» Т 0» 2 p / w0. В результате
. При затухании период Т затухающих колебаний, которые начались бы после прекращения действия вынуждающей силы, мало отличается от периода Т 0 собственных колебаний, т. е. Т» Т 0» 2 p / w0. В результате  , и
, и  . Подставим это значение b в выражение (1.4.6):
. Подставим это значение b в выражение (1.4.6): 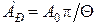 = 0,31 см.
= 0,31 см.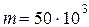 кг
u = 12 м/с
кг
u = 12 м/с
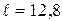 м
м
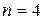
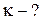
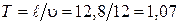 с, где
с, где 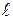 – длина рельса, u – скорость вагона. По условию период Т 0 собственных колебаний вагона связан с коэффициентом упругости, определяющим жесткость пружин рессоры по формуле:
– длина рельса, u – скорость вагона. По условию период Т 0 собственных колебаний вагона связан с коэффициентом упругости, определяющим жесткость пружин рессоры по формуле: 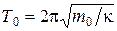 , и
, и 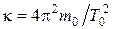 , где m 0 – масса вагона, приходящаяся на одну рессору. Считая, что на одну рессору приходится
, где m 0 – масса вагона, приходящаяся на одну рессору. Считая, что на одну рессору приходится  , получим m 0 = 12,5×103 кг. В результате жесткость пружины рессоры
, получим m 0 = 12,5×103 кг. В результате жесткость пружины рессоры 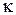 определится как
определится как (Н/м).
(Н/м).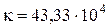 Н/м.
Н/м. . Найти скорость колебаний, смещение и резонансную частоту этого осциллятора. Коэффициент сопротивления жидкости считать равным r.
. Найти скорость колебаний, смещение и резонансную частоту этого осциллятора. Коэффициент сопротивления жидкости считать равным r.
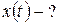
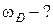
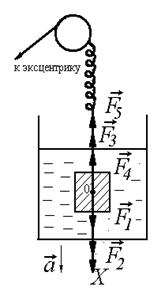 Рис. 1.4.3
Рис. 1.4.3
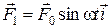 ; сила тяжести
; сила тяжести  ; сила Архимеда
; сила Архимеда 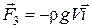 ; сила сопротивления жидкости
; сила сопротивления жидкости 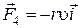 ; сила упругости пружины
; сила упругости пружины  ,
,  единичный вектор, направленный вдоль оси ОХ.
единичный вектор, направленный вдоль оси ОХ.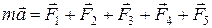 .
.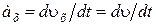 :
: , (1.4.8)
, (1.4.8) .
.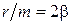 ,
, 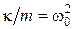 ,
, 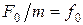 , получим дифференциальное уравнение:
, получим дифференциальное уравнение: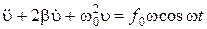 . (1.4.9)
. (1.4.9)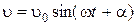 , (1.4.10)
, (1.4.10)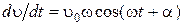 ,
, 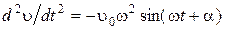 . Значения
. Значения  подставим в уравнение (1.4.10):
подставим в уравнение (1.4.10):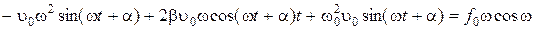 .
. в раскрытом виде:
в раскрытом виде: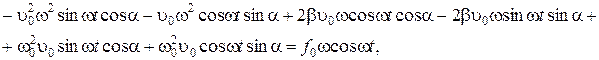
 (1.4.11)
(1.4.11) , а также коэффициенты при
, а также коэффициенты при  будут равны. В результате получим систему из двух уравнений, в которых неизвестными являются величины амплитуды скорости u0 и сдвиг фаз a:
будут равны. В результате получим систему из двух уравнений, в которых неизвестными являются величины амплитуды скорости u0 и сдвиг фаз a: , (1.4.12 а)
, (1.4.12 а) . (1.4.12 б)
. (1.4.12 б)
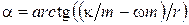 .
.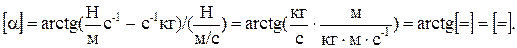
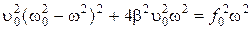 , тогда
, тогда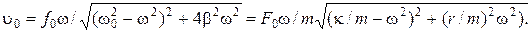
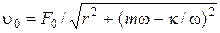 (1.4.13)
(1.4.13)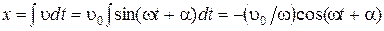 ,
, , где
, где 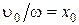 – амплитуда смещения х.
– амплитуда смещения х. (1.4.14)
(1.4.14)
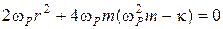 , и
, и 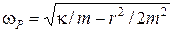 , что согласуется с (1.4.4).
, что согласуется с (1.4.4).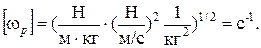
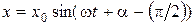 ,
,  . Скорость опережает по фазе вынуждающую силу F на a.
. Скорость опережает по фазе вынуждающую силу F на a.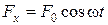 , шарик совершает установившиеся колебания. Найти: 1) среднюю за период колебания мощность < Р > силы F; 2) частоту вынуждающей силы, при которой < Р > максимальна; 3) величину максимальной мощности < Р >.
, шарик совершает установившиеся колебания. Найти: 1) среднюю за период колебания мощность < Р > силы F; 2) частоту вынуждающей силы, при которой < Р > максимальна; 3) величину максимальной мощности < Р >.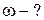 < Р >max –?
< Р >max –?
 , которая совершается вынуждающей силой за время dt:
, которая совершается вынуждающей силой за время dt: Рис. 1.4.4
Рис. 1.4.4
 (1.4.15)
(1.4.15)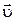 – скорость шарика. Определим скорость шарика. Проекция силы
– скорость шарика. Определим скорость шарика. Проекция силы  на ось ОХ изменяется по закону
на ось ОХ изменяется по закону  . Введем обозначения
. Введем обозначения  ,
, 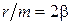 , тогда уравнение колебаний имеет вид:
, тогда уравнение колебаний имеет вид: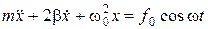 . (1.4.16)
. (1.4.16) . (1.4.17)
. (1.4.17)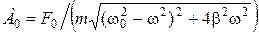 , (1.4.18)
, (1.4.18) . (1.4.19)
. (1.4.19)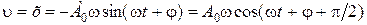 .
. .
. , а ее среднее значение за период равно
, а ее среднее значение за период равно 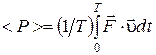 ,
, 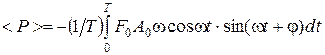 .
.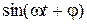 представим, используя тригонометрическую формулу для синуса суммы двух углов:
представим, используя тригонометрическую формулу для синуса суммы двух углов:  . Тогда получим
. Тогда получим 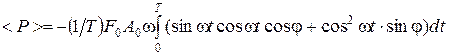 и
и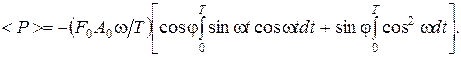
 ;
; 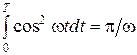 .
.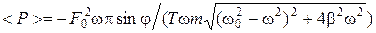 ,
, .
.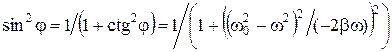 .
. .
.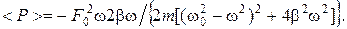
 (1.4.20)
(1.4.20)
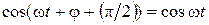 , и
, и 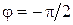 , а
, а  . Тогда, как следует из формулы (1.4.19),
. Тогда, как следует из формулы (1.4.19),  . Таким образом, скорость шарика и вынуждающая сила изменяются со временем без сдвига по фазе, если циклическая частота вынуждающей силы равна собственной частоте колебаний шарика. Следовательно, наибольшее значение средней мощности определяется из равенства (1.4.20), при
. Таким образом, скорость шарика и вынуждающая сила изменяются со временем без сдвига по фазе, если циклическая частота вынуждающей силы равна собственной частоте колебаний шарика. Следовательно, наибольшее значение средней мощности определяется из равенства (1.4.20), при 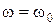 :
:  .
. ;
;  ;
;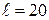 см. Коэффициент трения между стержнем и валиком равен m= 0,18. (рис. 1.4.5).
см. Коэффициент трения между стержнем и валиком равен m= 0,18. (рис. 1.4.5).

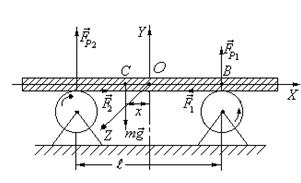 Рис. 1.4.5
Рис. 1.4.5
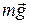 , а со стороны валиков действуют силы реакции
, а со стороны валиков действуют силы реакции 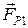 и
и  и силы трения
и силы трения 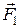 и
и  . Сумма проекций этих сил на ось ОY равна нулю:
. Сумма проекций этих сил на ось ОY равна нулю: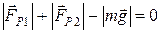 , (1.4.21)
, (1.4.21)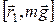 , направленный по оси ОZ и имеющий модуль
, направленный по оси ОZ и имеющий модуль  , т. к.
, т. к. 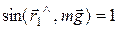 ,
, 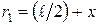 , и момент силы
, и момент силы 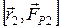 , направленный в сторону, противоположную оси ОZ и имеющий модуль
, направленный в сторону, противоположную оси ОZ и имеющий модуль 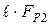 , т. к.
, т. к. 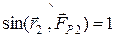 ,
, 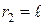 . В результате в проекции на ось ОZ получим
. В результате в проекции на ось ОZ получим 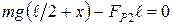 , отсюда
, отсюда  . Значение
. Значение 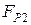 подставим в равенство (1.4.21) и найдем
подставим в равенство (1.4.21) и найдем 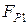 :
: 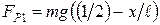 . Стержень проскальзывает относительно блоков, и силы трения определяются по формулам:
. Стержень проскальзывает относительно блоков, и силы трения определяются по формулам:  ,
,  .
.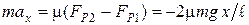 , иначе
, иначе  , или
, или 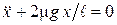 .
.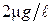 обозначим
обозначим 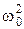 , т. е.
, т. е.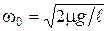 . (1.4.22)
. (1.4.22) – дифференциальное линейное однородное уравнение с постоянными коэффициентами. Решением этого уравнения будет гармоническая функция
– дифференциальное линейное однородное уравнение с постоянными коэффициентами. Решением этого уравнения будет гармоническая функция 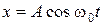 , где
, где 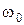 определяется из равенства (1.4.22). Стержень совершает гармонические колебания с периодом
определяется из равенства (1.4.22). Стержень совершает гармонические колебания с периодом  ,
, 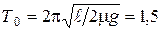 с.
с.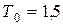 с.
с.
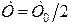 .
.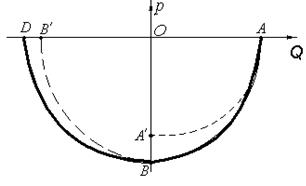 Рис. 1.4.7
Рис. 1.4.7
 Рис. 1.4.6
Рис. 1.4.6
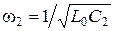 . Если закон изменения заряда
. Если закон изменения заряда 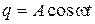 , то его колебательная скорость
, то его колебательная скорость  , а, следовательно, колебательный импульс
, а, следовательно, колебательный импульс 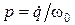 окажутся больше тех значений, которые они имели бы при неизменной частоте
окажутся больше тех значений, которые они имели бы при неизменной частоте  . В результате точка на фазовой плоскости будет двигаться не по окружности
. В результате точка на фазовой плоскости будет двигаться не по окружности  , а по эллипсу, вытянутому вдоль оси Р:
, а по эллипсу, вытянутому вдоль оси Р:  . В момент, когда фазовая точка пересекает ось Р, она окажется не в точке
. В момент, когда фазовая точка пересекает ось Р, она окажется не в точке 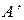 , лежащей на окружности радиуса А, а в точке В, отстоящей дальше от начала координат и лежащей на эллипсе. В этот момент по условию задачи емкость мгновенно увеличивается от значения С 2 до С 1, а частота w падает до значения w1 < w0. В результате движение точки происходит по эллипсу, вытянутому вдоль оси Q; его уравнение
, лежащей на окружности радиуса А, а в точке В, отстоящей дальше от начала координат и лежащей на эллипсе. В этот момент по условию задачи емкость мгновенно увеличивается от значения С 2 до С 1, а частота w падает до значения w1 < w0. В результате движение точки происходит по эллипсу, вытянутому вдоль оси Q; его уравнение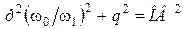 .
. Таким образом, движение точки на фазовой плоскости происходит по раскручивающейся спирали, происходит “раскачка” колебаний. Чтобы возникло параметрическое возбуждение колебаний, необходимо, чтобы период Т изменения параметра (емкости С) был связан с собственным периодом контура соотношением:
Таким образом, движение точки на фазовой плоскости происходит по раскручивающейся спирали, происходит “раскачка” колебаний. Чтобы возникло параметрическое возбуждение колебаний, необходимо, чтобы период Т изменения параметра (емкости С) был связан с собственным периодом контура соотношением: 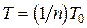 . В задаче n = 2, т. е.
. В задаче n = 2, т. е.  .
.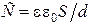 ) внешние силы преодолевают притяжение пластин, увеличивая расстояние d между ними. Энергия конденсатора вырастает на величину
) внешние силы преодолевают притяжение пластин, увеличивая расстояние d между ними. Энергия конденсатора вырастает на величину  , причем
, причем ,
,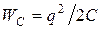 – энергия заряженного конденсатора. При увеличении емкости в точке В (сближение пластин) работа не производится, т. к. в этот момент
– энергия заряженного конденсатора. При увеличении емкости в точке В (сближение пластин) работа не производится, т. к. в этот момент 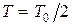 (участок фазовой траектории АВD) осциллятор теряет энергию:
(участок фазовой траектории АВD) осциллятор теряет энергию: 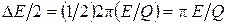 , где
, где 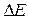 – потери энергии за период, Е – энергия осциллятора, Q – добротность осциллятора, в данном случае
– потери энергии за период, Е – энергия осциллятора, Q – добротность осциллятора, в данном случае 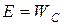 .
.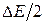 (за половину периода
(за половину периода  ), т. е.
), т. е. 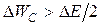 .
. имеет вид:
имеет вид: 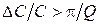 .
.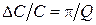 осциллятор совершает незатухающие колебания, его фазовая траектория становится окружностью, он выходит на предельный цикл.
осциллятор совершает незатухающие колебания, его фазовая траектория становится окружностью, он выходит на предельный цикл.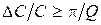 .
.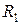
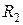 , x
, x
 Рис. 1.4.8
Рис. 1.4.8
 , или
, или  .
.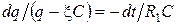 ;проинтегрируем:
;проинтегрируем: 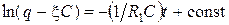 .
. .
. Рис. 1.4.9
Рис. 1.4.9
 , получим закон изменения напряжения на конденсаторе UС:
, получим закон изменения напряжения на конденсаторе UС: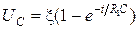 .
.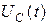 изображена на рис. 1.4.9. участком графика ОВ.
изображена на рис. 1.4.9. участком графика ОВ.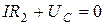 (RЛ << R 1);
(RЛ << R 1); 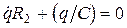 .
. и
и 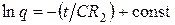 . Найдем const, учитывая, что при t = 0 заряд конденсатора q = q 0= CU 0, имеем
. Найдем const, учитывая, что при t = 0 заряд конденсатора q = q 0= CU 0, имеем  тогда
тогда  . Закон изменения напряжения на обкладках конденсатора при его разрядке через лампу Л имеет вид:
. Закон изменения напряжения на обкладках конденсатора при его разрядке через лампу Л имеет вид: 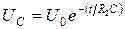 . Графически решение представлено участком кривой ВС на рис. 1.4.9. Разрядка происходит до тех пор, пока напряжение на обкладках конденсатора выше напряжения U Г гашения неоновой лампы. При U<U Г сопротивление R Л резко возрастает, ток через лампу прекращается, наступает процесс зарядки конденсатора.
. Графически решение представлено участком кривой ВС на рис. 1.4.9. Разрядка происходит до тех пор, пока напряжение на обкладках конденсатора выше напряжения U Г гашения неоновой лампы. При U<U Г сопротивление R Л резко возрастает, ток через лампу прекращается, наступает процесс зарядки конденсатора. . Энергия, запасенная в процессе зарядки конденсатора, полностью расходуется в процессе разрядки.
. Энергия, запасенная в процессе зарядки конденсатора, полностью расходуется в процессе разрядки. происходит вновь зарядка конденсатора до
происходит вновь зарядка конденсатора до 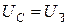 по закону
по закону  .
. IД –? UR –?
UL –? UC –?
IД –? UR –?
UL –? UC –?
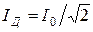 ,
, 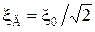 существует такое же соотношение как и для их амплитудных значений (1.4.6)
существует такое же соотношение как и для их амплитудных значений (1.4.6)
 . (1.4.23)
. (1.4.23)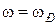 при которой знаменатель выражения (1.4.23) минимальный. Это соответствует резонансной частоте w Р, при которой обращается в нуль реактивное сопротивление
при которой знаменатель выражения (1.4.23) минимальный. Это соответствует резонансной частоте w Р, при которой обращается в нуль реактивное сопротивление 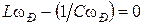 .
.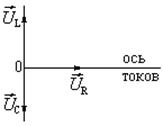 Рис. 1.4.11
Рис. 1.4.11
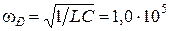 рад/с. При этом сила тока согласно (1.4.23) равна
рад/с. При этом сила тока согласно (1.4.23) равна 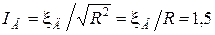 А.
А.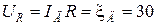 В;
В; 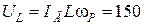 В;
В;  В.
В. и индуктивное
и индуктивное  сопротивления равны, напряжения на них изменяются в противофазе (рис. 1.4.11.) и равны по величине.
сопротивления равны, напряжения на них изменяются в противофазе (рис. 1.4.11.) и равны по величине. ;
;  А,
А,  В;
В;  В;
В;  В.
В.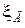 = 30 В, w= 1,00×105 рад/с.
= 30 В, w= 1,00×105 рад/с.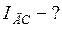
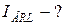
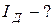

 А. В ветви 1 LR 2, где отсутствует емкостное сопротивление
А. В ветви 1 LR 2, где отсутствует емкостное сопротивление 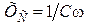 , действующая сила тока:
, действующая сила тока: А.
А.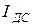 и
и  . Однако эти токи имеют различные фазы: между каждым из них и ЭДС существует сдвиг фаз, определяемых формулой (1.4.7):
. Однако эти токи имеют различные фазы: между каждым из них и ЭДС существует сдвиг фаз, определяемых формулой (1.4.7): 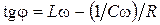 . Для ветви 1 С 2 R =0, L = 0, tgj C = – ¥, j C = –
. Для ветви 1 С 2 R =0, L = 0, tgj C = – ¥, j C = –  , получим
, получим 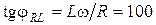 ;
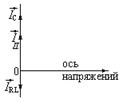
; 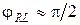 . (см. диаграмму токов на рис. 1.4.13).
. (см. диаграмму токов на рис. 1.4.13). – отстает по фазе от ЭДС на
– отстает по фазе от ЭДС на 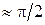 , т. к.
, т. к. 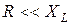 . В результате токи IC и
. В результате токи IC и  и
и 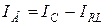 = 0,03 А.
= 0,03 А.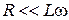 .
. А;
А; 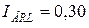 А;
А;  А.
А. . Вывести соотношение между амплитудными значениями тока I 0 и напряжения
. Вывести соотношение между амплитудными значениями тока I 0 и напряжения 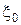 . Найти сдвиг по фазе между напряжением и током.
. Найти сдвиг по фазе между напряжением и током.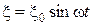
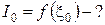 j –?
j –?
 . (1.4.24)
. (1.4.24)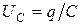 . Согласно условию (1.4.24)
. Согласно условию (1.4.24)  , отсюда
, отсюда  . Полученное равенство продифференцируем по времени и учтем, что
. Полученное равенство продифференцируем по времени и учтем, что 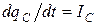 :
:

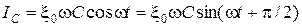 . (1.4.25)
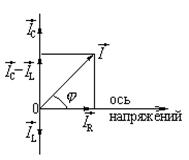
. (1.4.25)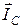 , направлен вверх и составляет угол
, направлен вверх и составляет угол 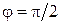 с осью напряжений.
с осью напряжений.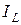 через
через


