Краткие теоретические сведения. Если на осциллятор кроме упругой силы и сил сопротивления действует еще добавочная периодическая сила
Если на осциллятор кроме упругой силы и сил сопротивления действует еще добавочная периодическая сила В этом случае уравнение колебаний осциллятора имеет вид: или если ввести обозначения: В результате действия всех сил получится колебание, частота которого совпадает с частотой w вынуждающей силы, и решение уравнения колебаний (1.4.1.) запишется так: где w – частота вынуждающей силы, А – амплитуда смещения, a – сдвиг по фазе между смещением S и силой Эти величины определяются из следующих выражений:
Из равенства (1.4.3) следует, что смещение отстает по фазе от вынуждающей силы. Амплитуда А (1.4.2) и сдвиг по фазе a (1.4.3) между смещением и силой зависят от соотношения частоты w вынуждающей силы и частоты собственных колебаний осциллятора. Амплитуда вынужденных колебаний достигает максимума при резонансной частоте при w=w Р, удовлетворяющей соотношению: Максимальная (резонансная) амплитуда АР достигает значения: которое получается, если значение w Р из формулы (1.4.4) подставить в выражение (1.4.2). Если сопротивление среды мало (b= 0), то согласно (1.4.4) w Р = w0, а АР ® ¥, как следует из формулы (1.4.5). В условиях резонанса сдвиг по фазе между смещением и силой определяется выражением: В колебательном контуре вынужденные колебания возникают, например, если включить последовательно с элементами контура LCR переменную ЭДС (подать переменное напряжение U = U 0cosw t)
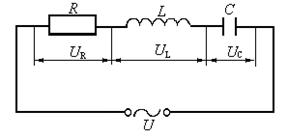
Колебательный контур, в котором элементы R, L, C включены параллельно, подробно рассматривается в задаче 10 этого раздела. В цепи, схема которой приведена на рис. 1.4.1, установятся вынужденные колебания тока I той же частоты w, как и у переменной ЭДС, по закону: I = I 0 cos (w t – j).
Величина амплитуды I 0 тока и j – сдвиг по фазе между током и напряжением определяются по формулам:
если элементы R, L, C включены в контур последовательно с источником напряжения. Соответствующая векторная диаграмма напряжений показана на рис. 1.4.2 при этом Напряжения в цепи переменного тока складываются по правилу сложения векторных величин с учетом угла (разности фаз) между векторами Закон (1.4.6) можно рассматривать как закон Ома для амплитудных значений тока и напряжения для цепи переменного тока с последовательным соединением R, L, C с источником ЭДС, если величину Сопротивление где Мощность, выделяемая в цепи переменного тока при сдвиге фазы j, равна где
В любой момент времени для квазистационарного тока имеют место законы Кирхгофа, установленные для постоянных токов:
Для токов в произвольной электрической цепи можно, используя правила Кирхгофа, записать систему дифференциальных уравнений, решение которой позволит определить токи и напряжения в цепи как функцию времени. Система, которая сама регулирует поступление энергии от внешнего источника так, чтобы поддерживать режим незатухающих колебаний, называется автоколебательной. Параметрические колебания возбуждаются путем периодического изменения величины параметра, определяющего собственную частоту осциллятора.
|

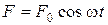 , то возникают вынужденные колебания.
, то возникают вынужденные колебания.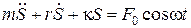 ,
, , (1.4.1)
, (1.4.1)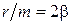 ,
, 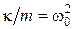 ,
, 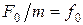 .
.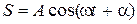 ,
,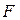 .
.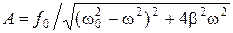 , (1.4.2)
, (1.4.2)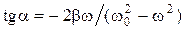 . (1.4.3)
. (1.4.3) . (1.4.4)
. (1.4.4)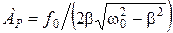 , (1.4.5)
, (1.4.5)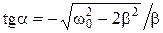 . При b® 0
. При b® 0  , а
, а  .
.
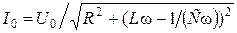 , (1.4.6)
, (1.4.6)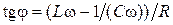 , (1.4.7)
, (1.4.7)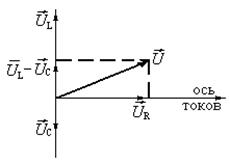 Рис. 1.4.2
Рис. 1.4.2
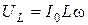 ;
; 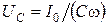 ,
, 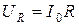 .
.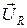 ,
, 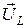 ,
, 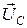 . Амплитуда I 0 тока при последовательном соединении в цепи (рис. 1.4.1) достигает максимального значения (явление резонанса), если частота w вынужденных колебаний совпадает с частотой w0 свободных незатухающих колебаний
. Амплитуда I 0 тока при последовательном соединении в цепи (рис. 1.4.1) достигает максимального значения (явление резонанса), если частота w вынужденных колебаний совпадает с частотой w0 свободных незатухающих колебаний 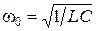 .
.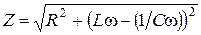 считать полным сопротивлением цепи.
считать полным сопротивлением цепи.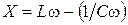 называется реактивным сопротивлением,
называется реактивным сопротивлением,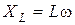 – индуктивное,
– индуктивное, 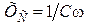 – емкостное сопротивление цепи.
– емкостное сопротивление цепи.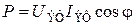 ,
, и
и  – эффективные (действующие) значения напряжения и силы тока:
– эффективные (действующие) значения напряжения и силы тока: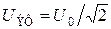 ,
, 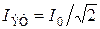 .
.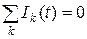 ,
, 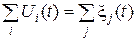 .
.


