Введение. Для наблюдения процесса восстановления вынужденных электрических колебаний в колебательном контуре с начальным запасом энергии
Пусть в начальный момент времени ток в контуре нарастает (рис.1). Выбрав направление обхода контура по часовой стрелке, запишем второе правило Кирхгофа:
U R+ U C= e s+ e,(1) где: U R – напряжение на сопротивлении R; UC – напряжение на конденсаторе С; e s – эдс самоиндукции в катушке индуктивности L; e - внешняя ЭДС. Учитывая, что
Разделив (2) на L и введя обозначения R/L = 2b, 1/(LC) = w02, получим неоднородное дифференциальное уравнение:
где β – коэффициент затухания; w0 – собственная частота коле-бательного контура. Решение этого неоднородного дифференциального уравнения равно сумме
и частного решения неоднородного уравнения q2(t), где qm/, α/, ω/- соответственно амплитуда заряда, начальная фаза и циклическая частота затухающих колебаний.
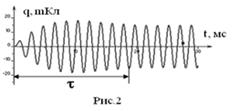 Но q1(t) играет роль только в течение времени τ; востановления колебаний, т.е. t≤τ; (рис.2), в дальнейшем Но q1(t) играет роль только в течение времени τ; востановления колебаний, т.е. t≤τ; (рис.2), в дальнейшем (t> τ) q=q2(t). Частное решение уравнения (4) имеет вид:
где ψ – разность фаз между колебаниями заряда и внешней ЭДС. Сила тока в контуре:
Напряжение на конденсаторе
Напряжение на сопротивлении
Величина напряжения на катушке UL индуктивности равна ЭДС самоиндукции εs, направление которой зависит от направления тока в контуре и от скорости его изменения
Представим уравнение (1)в виде UR+UC+ UL= emcos wt и подставим в него уравнения (5)-(8):
Величины, стоящие в (9) перед косинусами, представим в виде векторов, а их фазовые соотношения указаны в аргументах. На основании (9) построим векторную диаграмму (рис.3), из которой следует, что em2 = (ULm-UCm)2 + URm2 = Im2((wL - 1/(wC))2+R2),а амплитуда тока
где контура (импеданс); ωL=XL и 1/(ωC)=XC – соответственно индуктивное и емкостное сопротивление контура.
Из векторной диаграммы
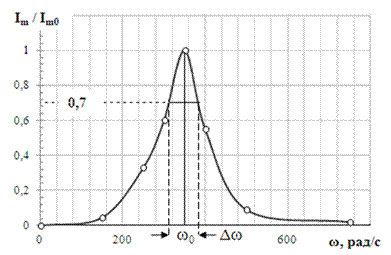
Из анализа (12) следует: 1) если XL> XC (w> w0), то ток отстает по фазе от приложенного ЭДС на j; 2) если XL< XC (w< w0), то ток опережает по фазе приложенное ЭДС на j; 3) если XL=XC (w = w0), то ток совпадает по фазе с приложенным ЭДС. При равенстве индуктивного и емкостного сопротивлений XL=XC наступает резонанс, при котором величина тока в контуре достигает максимального значения Im0 (см.(10)). Разделим ампли-туду тока Im при любой частоте на Im0 и построим график зависи-мости Im/ Im0(ω) (рис.4). Из этого графика можно определить Рис. 4 ширину полосы пропускания Δω; контура, которая берется на высоте 0,7. При небольшом коэффициенте затухания β добротность Q колебательного контура можно определить путем деления резонансной частоты ω0 на ширину полосы пропускания Δω:
или с помощью параметров контура, по формуле:
О программе
Программа наглядно иллюстрирует физические процес-сы, протекающие в колебательном контуре при вынужденных колебаниях. Разработана студентами факультета «Автоматизация и информатика» Бондаренко Владимиром и Антоновым Антоном.
Подготовка к эксперименту
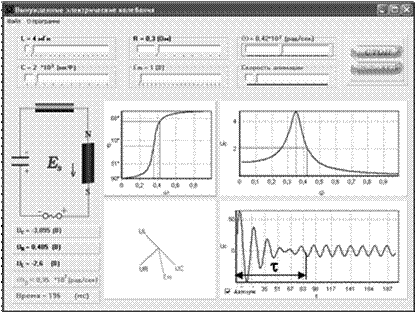
1. Открыть папку «Вынужденные электрические колебания» и файл «Resonans.ехе». 2. Познакомиться с рабочей панелью (рис.5).
Рис. 5 3. В четырех окнах рабочей панели представлены (слева направо): фазовая зависимость от частоты между током в контуре и внешней ЭДС;зависимость амплитуды напряжения UC на конденсаторе от частоты; векторная диаграмма; временная развертка текущего напряжения на конденсаторе. 4. В верхней части панели расположены органы управления, с помощью которых устанавливают: величину индуктивности L, электроемкости C и сопротивления контура R; циклическую частоту ω и амплитуду εm внешней ЭДС; скорости анимации. 5. В левой части панели расположена модель колебательного контура, с помощью которой отображаются в динамике полярность напряжений на конденсаторе и внешней ЭДС, направление эдс самоиндукции в катушке индуктивности и направление магнитного поля. 6. Под контуром отображается: текущее значение напряжений на конденсаторе, сопротивлении и катушке индуктивности; циклическая частота собственных колебаний контура; время эксперимента. 7. С помощью регуляторов «С», «L», «Em», «ω» установить на рабочей панели: 1) электроемкость конденсатора из интервала 1 – 10 мкФ; 2) индуктивность катушки из интервала 3-20 мГн; 4) амплитуду внешней ЭДС из интервала 1-10В. 8. Установить флажок в окошке «Автозум».
Проведение эксперимента Задание 1. Исследование влияния внешней ЭДС и сопротивления колебательного контура на его характеристики. 1. Установить частоту ω внешней ЭДС примерно в два раза меньше ω0. 2. Для выбранной частоты вычислить индуктивное сопротивление (XL=ωL) и емкостное сопротивление (XC=1/(ωC). 3. Установите первое значение сопротивления контура 4. Вычислить: полное сопротивление контура по формуле (11); добротность контура по формуле (14); разность фаз между током в контуре и внешней ЭДС φ; по формуле (12). 5. Запустите программу в работу клавишей «Пуск» и, наблюдая за временной разверткой U(t), дождитесь начала вынужденных колебаний с постоянной амплитудой. Остановите работу прог-раммы клавишей «Пауза». По оси времени t измерьте время τ; восстановления вынужденных колебаний (см. рис.5). 6. Продолжить работу программы (клавишей «Продолжить») и остановить (клавишей «Пауза») в момент, когда напряжение на конденсаторе достигнет амплитудного значения Um. 7. Вычислить амплитудное значение тока в контуре 8. Повторить пункты 4 – 8 для сопротивлений контура R=0,5 и 0,9 Ом. 9. Результаты измерений и вычислений занести в табл. 1. Таблица 1
10. Повторить пункты 2 – 9 для частот вынужденных колебаний ω > ω0 и ω ≈ ω0. 11. По выполненному заданию сделать вывод.
Задание 2. Определение полосы пропускания колебательного контура
1. Установить сопротивление контура из интервала 2. Выбрать по три значения ω, отличающихся от ω0 примерно на 15, 30 и 45%, как в большую, так и в меньшую сторону. 3. Вычислить для каждой ω индуктивное XL, емкостное XC сопротивление и импеданс Z колебательного контура. 4. Установите первое значение циклической частоты ω. 5. Запустите программу в работу клавишей «Пуск» и, дождавшись начала вынужденных колебаний с постоянной амплитудой, остановите (клавишей «Пауза») работу программы в момент, когда напряжение на конденсаторе достигнет амплитудного значения Um. 6. Вычислите амплитудное значение тока в контуре 7. Повторите пункты 5 – 6 для остальных циклических частот. 8. Каждое значение амплитуды тока разделить на максимальную амплитуду тока Im0, соответствующую резонансной частоте ω0. 9. Результаты измерений и вычислений занести в табл. 2. Таблица 2
10. Построить график зависимости Im/ Im0(ω). 11. На уровне 0,7 графика определить полосу пропускания Δω колебательного контура, а по формуле (13) вычислить доброт-ность контура. 12. По выполненному заданию сделать вывод.
Контрольные вопросы
1. Какие физические процессы протекают в колебательном контуре? 2. Приведите дифференциальное уравнение вынужденных колебаний в реальном колебательном контуре и его решение? 3. Перечислите основные характеристики реального колеба-тельного контура: L, C, R, ω0, β, Q. 4. Как с помощью векторной диаграммы определить амплитуду тока в контуре и фазовые соотношения между током и внешней ЭДС? 5. В каких случаях ток в колебательном контуре отстает, опере-жает или совпадает по фазе по отношению к внешней ЭДС? 6. Как по резонансной кривой для силы тока определить ширину полосы пропускания колебательного контура? 7. Как можно определить добротность колебательного контура?
Рекомендуемая литература 1. СавельевИ.В. Курс физики. Т2. / И.В. Савельев. – М.: Наука, 1989. §§70,71. 2. Трофимова Т.И. Курс физики / Т.И. Трофимова. – М.: Высшая школа, 2003. §§ 146-148. 3. Яворский В. М. Справочник по физике / В.М. Яворский, А.А. Детлаф. – М.: Наука, 1985. § IV.2.1.
Составители: Кудря А.П., Бондаренко В.В., Антонов А.И., Шполянский А.Я.
Лабораторная работа № 19В
|

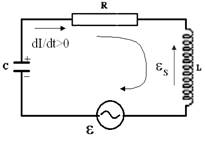 Для наблюдения процесса восстановления вынужденных электрических колебаний в колебательном контуре с начальным запасом энергии, необходимо в его разрыв подключить внешний источник с ЭДС (рис.1), изменяющийся по гармоническому закону:
Для наблюдения процесса восстановления вынужденных электрических колебаний в колебательном контуре с начальным запасом энергии, необходимо в его разрыв подключить внешний источник с ЭДС (рис.1), изменяющийся по гармоническому закону: 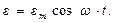
 , а в уравнении (1)
, а в уравнении (1) 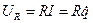 ,
, 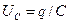 ,
, 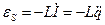 , перепишем его в виде:
, перепишем его в виде: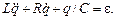 (2)
(2)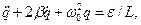 (3)
(3) общего решения соответствующего однородного уравнения
общего решения соответствующего однородного уравнения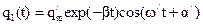
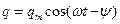 , (4)
, (4) (5)
(5)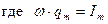 - амплитуда тока в контуре, а
- амплитуда тока в контуре, а 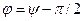 – разность фаз между током и внешней ЭДС.
– разность фаз между током и внешней ЭДС.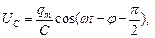 (6)
(6)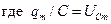 – амплитуда напряжения на конденсаторе.
– амплитуда напряжения на конденсаторе.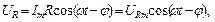 (7)
(7)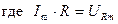 – амплитуда напряжения на сопротивлении.
– амплитуда напряжения на сопротивлении.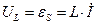 :
: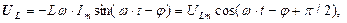 (8)
(8)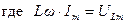 – амплитуда напряжения на катушке.
– амплитуда напряжения на катушке.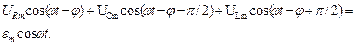 (9)
(9) (10)
(10)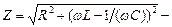 полное сопротивление (11)
полное сопротивление (11)
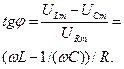 (12)
(12)
 (13)
(13)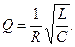 (14)
(14)