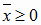Показатели работы отраслей
Балансовый характер этой таблицы выражается в том, что при любом i = l,..., n должно выполняться соотношение
означающее, что валовой выпуск xi расходуется на производственное потребление, равное x i1 + xi 2 +...+ xin, и непроизводственное потребление, равное уi. Будем называть (1.1) соотношениями баланса. Для выпуска любого объёма хj продукции отрасли j необходимо затратить продукцию отрасли i в качестве aij x j, где аij - постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объёму производимой продукции. Это допущение постулирует, как говорят, линейность существующей технологии.
Коэффициенты аij называют коэффициентами прямых затрат (коэффициент материалоемкости). В предположении линейности соотношения (1.1) принимают вид: x 1 = a 11 x 1 + a 12 x 2 +... + a 1 n xn + y 1 x 2 = a 21 x 1 + a 22 x 2 +... + a 2 n xn + y 2 ......................................... xn = an 1 x 1 + an 2 x 2 +... + ann xn + yn, или, в матричной записи,
где
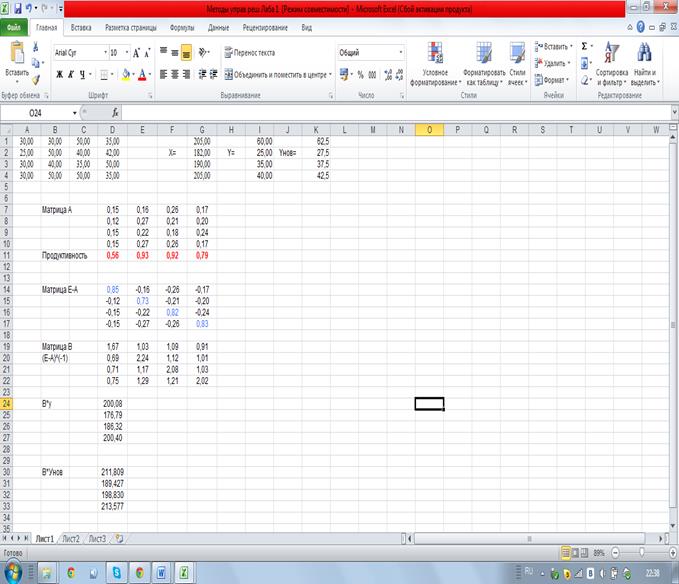
Вектор Уравнения межотраслевого баланса можно использовать для целей планирования. В этом случае задача ставится так: для предстоящего планового периода [ T 0, T 1] задается вектор При этом нужно иметь в виду следующие особенности системы (1.3):
1. Все компоненты матрицы А и вектора 2. Все компоненты вектора
Из матричного уравнения (1.3) сразу следует:
3. Решение задачи
4. Анализ результатов
Матрица прямых затрат продуктивна, так как каждое значение не должно превосходить 1 (0.56<1, 0.93<1, 0.92<1, 0.79<1). Валовый продукт, соответствующий увеличению конечного продукта на 2,5%, был рассчитан.
|

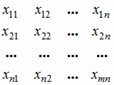
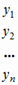
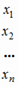
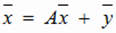 ,
,
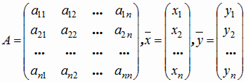
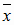 называется вектором валового выпуска, вектор
называется вектором валового выпуска, вектор 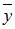 - вектором конечного потребления, а матрица А - матрицей прямых затрат. Соотношение (1.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов
- вектором конечного потребления, а матрица А - матрицей прямых затрат. Соотношение (1.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов 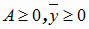 .
.