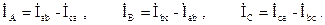Соединение фаз нагрузки звездой
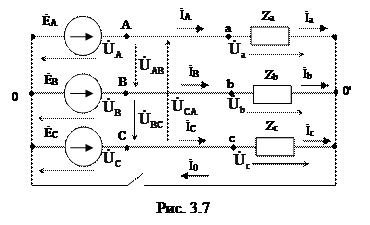
При соединении фаз генератора и нагрузки по схеме «звезда-звезда» (рис. 3.7) провод 0'0, соединяющий нулевую точку трехфазного источника с нулевой точкой приемника (рис. 3.7), называется нулевым или нейтральным. Существуют четырехпроводная (с нулевым проводом – ключ замкнут) и трехпроводная (без нулевого провода - ключ разомкнут) схемы соединения фаз трехфазной нагрузки.
Напряжение между нулевой точкой генератора и нулевой точкой приёмника называется напряжением смещения нейтрали  . При условии, что потенциал нулевой точки генератора равен нулю, напряжение смещения нейтрали определяется по методу двух узлов . При условии, что потенциал нулевой точки генератора равен нулю, напряжение смещения нейтрали определяется по методу двух узлов
Фазные напряжения приемника при соединении фаз по схеме звезда определяются:
Линейные напряжения равны разности соответствующих фазных напряжений приемника:
Фазные токи определяются по закону Ома:
Ток нейтрального провода для четырехпроводных цепей определяется согласно первому закону Кирхгофа как сумма фазных токов: При соединении фаз приемников по схеме «звезда» токи, протекающие по линейным проводам IЛ, равны токам в фазах приемника IФ
Схема с нулевым проводом. В случае, если сопротивление нулевого провода равно нулю (рис. 3.7- ключ замкнут), потенциалы нулевой точки генератора и приемника равны между собой
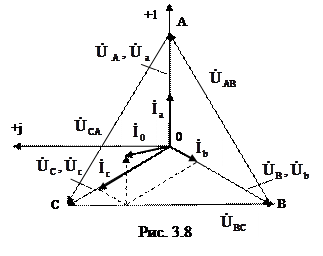
Наличие нулевого провода при неравномерной нагрузке фаз обеспечивает независимость режима работы одной фазы от другой. Линейные напряжения будут связаны с фазными соотношением UЛ= Фазные токи определяются по закону Ома: Ток нейтрального провода для четырехпроводных цепей определяется согласно первому закону Кирхгофа как сумма фазных токов: Векторная диаграмма напряжений и токов для случая неравномерной активной нагрузки Rа ≠ Rb ≠ Rc приведена на рис. 3.8.
В частном случае при симметричной нагрузке фаз приемника, когда Zа=Zb=Zc = zejφ, ток в нулевом проводе нет:
так как
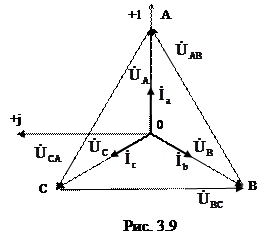
Векторная диаграмма напряжений и токов для случая симметричной активной нагрузки Rа=Rb= Rc приведена на рис. 3.9. Схема без нулевого провода. Потенциал нулевой точки приемника в схеме без нулевого провода (рис. 3.7- ключ разомкнут) отличается от потенциала нулевой точки генератора. Напряжение между этими точками - напряжение смещения нейтрали
Фазные напряжения приемников в этом случае рассчитываются:
То есть фазные напряжения приемников отличаются от соответствующих фазных напряжений генератора на величину напряжения смещения нейтрали. Линейные напряжения при любом распределении нагрузок между фазами сохраняют симметричный характер и остаются неизменными. Фазные токи определяются по закону Ома: Сумма фазных токов в трехпроводной цепи равна нулю
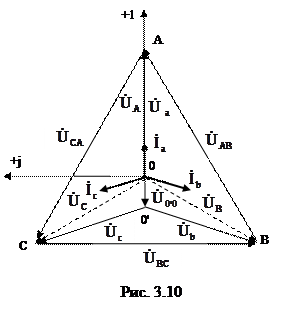
Векторная диаграмма напряжений и токов для случая неравномерной активной нагрузки Rа ≠ Rb ≠ Rc приведена на рис. 3.10. В частном случае при симметричной нагрузке фаз приемника, когда Zа= Zb = Zc = zejφ, напряжение смещения нейтрали будет равно нулю:
так как То есть потенциал нулевой точки приемника и нулевой точки генератора равны. Тогда фазные напряжения приемников будут равны фазным напряжениям генератора, как и в схеме с нулевым проводом. Таким образом, в симметричной трехфазной системе нулевой провод оказывается лишним.
Соединение фаз нагрузки треугольником При соединении фаз нагрузки по схеме «треугольник» (рис. 3.11) обеспечивается независимость работы фаз друг от друга, так как к фазам подводятся непосредственно линейные напряжения сети, то есть линейные напряжения равны соответствующим фазным напряжениям приемников: UЛ = UФ. Линейные напряжения генератора одинаковы по модулю и сдвинуты друг относительно друга по фазе на 120°. Учитывая это, можно записать:
По линейным проводам протекают линейные токи, положительное направление которых от генератора к нагрузке. Линейные токи рассчитываются с помощью первого закона Кирхгофа:
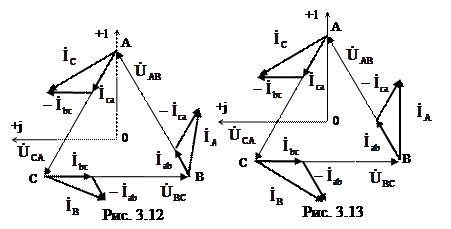
Векторная диаграмма напряжений и токов для случая неравномерной активной нагрузки Rаb ≠ Rbc ≠ Rca приведена на рис. 3.12. В частном случае при симметричной нагрузке фаз приемника, когда Zа= Zb = Zc = zejφ, фазные токи нагрузки одинаковы по модулю и сдвинуты друг относительно друга по фазе на угол 120°.
Линейные токи при симметричной нагрузке также одинаковы по модулю и сдвинуты относительно друг друга по фазе на 120°. Это хорошо видно на векторной диаграмме (рис. 3.13), Причем линейные и фазные токи приемника при симметричной нагрузке связаны соотношением
IЛ= 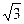 IФ. IФ.
|

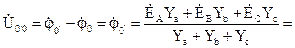
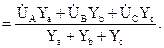

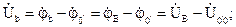
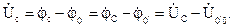

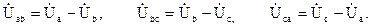
 .
.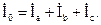
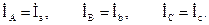
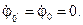 Тогда фазные напряжения приемников равны соответствующим фазным напряжениям генератора при любых нагрузках фаз:
Тогда фазные напряжения приемников равны соответствующим фазным напряжениям генератора при любых нагрузках фаз: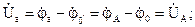


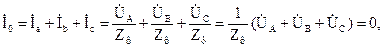
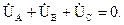
 , которое определяется по методу двух узлов:
, которое определяется по методу двух узлов: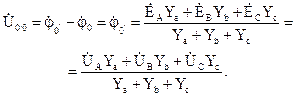
 .
.
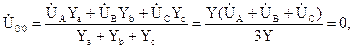
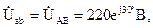
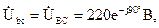

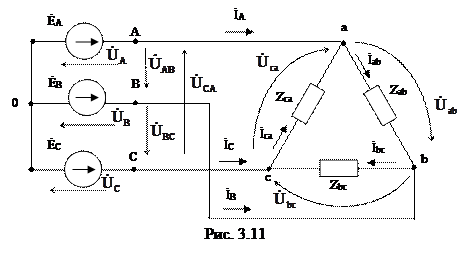
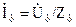 .
.