Математический анализ
3.1 Множества. Операции над множествами. Числовые множества. 3.2 Функции одной переменной: определение, график функции, способы задания, основные характеристики функции. Понятие сложной и обратной функции. 3.3 Графики и свойства основных элементарных функций. Метод сдвига и деформации при построении графиков. 3.4 Предел функций в точке, предел функций при 3.5 Основные теоремы о функциях имеющих предел. 3.6 Бесконечно малые и бесконечно большие функции, их связь и свойства. Теорема о связи функции, её предела и бесконечно малой функции. 3.7 Эквивалентные бесконечно малые функции 3.8 Математические неопределенности. Раскрытие математических неопределенностей. 3.9 Замечательные пределы, их применение при раскрытии математических неопределенностей. 3.10 Непрерывность функции в точке. Классификация точек разрыва. Свойства непрерывных функций. 3.11 Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке. 3.12 Приращение функции и аргумента функции в данной точке. Понятие производной функции, её геометрический и механический смысл. Уравнения касательной и нормали к графику функции. 3.13 Основные правила дифференцирования. Производные некоторых элементарных функций (их нахождение на основе определения). Таблица производных. 3.14 Понятие дифференцируемой функции. Критерий дифференцируемости. Необходимое и достаточное условия дифференцируемости функции. 3.15 Дифференциал функции, его геометрический смысл. Свойство инвариантности формы первого дифференциала функции. Свойства дифференциалов. 3.16 Производные и дифференциалы высших порядков, их свойства. Механический смысл второй производной. 3.17 Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа, Коши. 3.18 Правила Лопиталя (применение дифференциального исчисления к вычислению пределов). 3.19 Условия возрастания и убывания функции на промежутке. Необходимые и достаточные условия существования точек экстремума. 3.20 Выпуклость вверх и вниз, точки перегиба графика функции 3.21 Асимптоты графика функции. 3.22 Общая схема исследования функций и построения графиков. 3.23 Первообразная. Неопределенный интеграл и его свойства. 3.24 Таблица основных неопределенных интегралов. 3.25 Условия интегрируемости функций. 3.26 Основные методы интегрирования: метод непосредственного интегрирования, замена переменной в неопределенном интеграле, интегрирование по частям. 3.27 Интегрирование рациональных дробей: разложение дробной рациональной функции на простейшие дроби, интегрирование простейших рациональных дробей, интегрирование рациональных функций. 3.28 Интегрирование выражений, содержащих тригонометрические функции. 3.29 Интегрирование некоторых иррациональностей. 3.30 Определенный интеграл и его основные свойства. Геометрический смысл определенного интеграла. 3.31 Теорема о производной интеграла по верхнему переменному пределу интегрирования. Формула Ньютона-Лейбница. 3.32 Замена переменной в определенном интеграле. Интегрирование по частям определенного интеграла. 3.33 Несобственные интегралы первого и второго рода. 3.34 Геометрические приложения определенного интеграла. Вычисление длины дуги, площади плоской фигуры, объема тела вращения. 3.35 Определение функции нескольких переменных, геометрическое изображение функции двух переменных. 3.36 Предел, непрерывность функции нескольких переменных. 3.37 Частные производные функции двух переменных. 3.38 Дифференцируемость функции нескольких переменных. Необходимые и достаточные условия дифференцируемости. 3.39 Полный дифференциал. Свойство инвариантности формы первого полного дифференциала функции нескольких переменных. 3.40 Производная сложной и неявно заданной функции. 3.41 Частные производные и дифференциалы высших порядков. 3.42 Производная по направлению, градиент функции нескольких переменных. 3.43 Экстремумы функции двух переменных, необходимые и достаточные условия существования точек экстремума. 3.44 Условный экстремум. Метод множителей Лагранжа. 3.45 Наименьшее и наибольшее значения функции нескольких переменных в замкнутой области. 3.46 Двойной интеграл: определение, свойства, вычисление. 3.47 Тройной интеграл: определение, свойства, вычисление. 3.48 Криволинейный интеграл: определение, свойства, вычисление. Формула Грина. 3.49 Определение дифференциального уравнения. Порядок дифференциального уравнения. Начальные условия, задача Коши. Общее и частное решения. Общий и частный интеграл. Интегральная кривая. 3.50 Теорема существования и единственности решения уравнения 3.51 Дифференциальное уравнение первого порядка. 3.52 Дифференциальные уравнения с разделенными и разделяющимися переменными. Понятие особого решения. 3.53 Однородные уравнения первого порядка. 3.54 Линейное уравнение первого порядка. 3.55 Уравнения Бернулли. 3.56 Уравнения в полных дифференциалах. 3.57 Решение дифференциального уравнения вида 3.58 Дифференциальные уравнения, допускающие понижение порядка. Методы их решения. 3.59 Линейно зависимые и линейно независимые системы функций. 3.60 Определитель Вронского. Теорема о линейной зависимости системы функций. 3.61 Линейные однородные дифференциальные уравнения n -го порядка с постоянными коэффициентами. Теорема о структуре общего решения. Метод Эйлера. 3.62 Линейные неоднородные дифференциальные уравнения n -го порядка с постоянными коэффициентами. Теорема о структуре общего решения. Метод Лагранжа. 3.63 Линейное неоднородное дифференциальное уравнения n -го порядка со специальной правой частью. Метод неопределенных коэффициентов. 3.64 Определение системы дифференциальных уравнений. Начальные условия, задача Коши. Общее и частное решения системы дифференциальных уравнений. 3.65 Нормальная система дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. 3.66 Решение системы линейных однородных уравнений методом Эйлера. 3.67 Решение системы линейных однородных и неоднородных уравнений методом исключения. 3.68 Алгебраическая форма комплексного числа. Действия с комплексными числами в алгебраической форме. 3.69 Геометрическое изображение комплексного числа. Аргумент и модуль комплексного числа. 3.70 Тригонометрическая форма комплексного числа. Действия с комплексными числами в тригонометрической форме. 3.71 Показательная форма комплексного числа. Действия с комплексными числами в показательной форме. 3.72 Функция комплексного переменного. 3.73 Предел функции комплексного переменного. Непрерывность. 3.75 Дифференцируемая функция. Необходимые и достаточные условия дифференцируемости функции комплексного переменного. Аналитическая (регулярная) функция. Производная от функции комплексного переменного. 3.76 Гармонические функции. Связь аналитических функций с гармоническими. 3.77 Элементарные функции комплексного переменного: показательная функция, логарифмическая функция, тригонометрические функции, обратные тригонометрические функции. Гиперболические функции. 3.78 Интеграл от функции комплексного переменного. Способы вычисления. Свойства. 3.79 Теорема Коши для односвязной области. Следствия. 3.80 Теорема Коши для многосвязной области. Следствия. 3.81 Интегральная формула Коши. Производные высших порядков аналитической функции. 3.82 Изолированные особые точки. Классификация изолированных особых точек. 3.83 Вычеты. Основная теорема о вычетах. 3.84 Вычет относительно устранимой особой точки. 3.85 Вычет относительно полюса. 3.86 Понятие оригинала и изображения по Лапласу. Изображение единичной функции Хевисайда. Теорема существования изображения. 3.87 Свойства преобразования Лапласа. 3.88 Свойство линейности. 3.89 Теорема подобия. 3.90 Теорема смещения. 3.91 Дифференцирование оригинала. 3.92 Дифференцирование изображения. 3.93 Интегрирование оригинала. 3.94 Интегрирование изображения. 3.95 Теорема запаздывания. 3.96 Свертка двух функций. Интеграл Дюамеля. 3.97 Способы восстановления оригинала по известному изображению. 3.98 Решение обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений операционным методом.
|

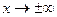
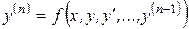 (формулировка).
(формулировка). .
.


