E.2.7. Двоичные деревья
В упражнениях 1-27 использовать двоичные деревья при следующем их описании. type ТЭД=...: {тип элементов дерева} дерево= вершина; вершина=record элем:ТЭД; лев, прав: дерево end; В этих упражнениях Т, 1. Создать и продемонстрировать работу программы, которая определяет, входит ли элемент Е в дерево Т. 2. Создать и продемонстрировать работу программы, которая определяет число вхождений элемента Е в дерево Т. 3. Создать и продемонстрировать работу программы, которая вычисляет сумму элементов непустого дерева Т (ТЭД=real). 4. Создать и продемонстрировать работу программы, которая находит величину наибольшего элемента непустого дерева Т (ТЭД=real). 5. Создать и продемонстрировать работу программы, которая печатает элементы из всех листьев дерева Т (ТЭД=char). 6. Создать и продемонстрировать работу программы, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от корня дерева до листьев. 7. Создать и продемонстрировать работу программы, которая подсчитывает число вершин на n-ом уровне непустого дерева Т (корень считать вершиной 0-го уровня). 8. Рекурсивно и не рекурсивно создать и продемонстрировать работу логической функции equal (T1,T2), проверяющую на равенство деревья Т1 и Т2. 9. Создать и продемонстрировать работу процедуры copy(Т, Т1), которая строит Т1 - копию дерева Т. 10. Создать и продемонстрировать работу процедуры create(T,n), где n - положительное целое число, которое строит дерево Т, показанное на рис. 9.1.
11. Создать и продемонстрировать работу логической функции same(T), определяющую, есть ли в дереве Т хотя бы два одинаковых элемента. 12. Формулу вида <формула>::= <терминал> ï (<формула><знак><формула>) <знак>:: = + ï - ï * <терминал>::= 0 ï 1 ï 2 ï 3 ï 4 ï 5 ï 6 ï 7 ï 8 ï 9 можно представить в виде двоичного дерева ("дерева-формулы") с ТЭД=char согласно следующим правилам: формула из одного терминала (цифры) представляется деревом из одной вершины с этим терминалом, а формула вида (f1 s f2) - деревом, в котором корень - это знак s, а левое и правое поддеревья - это соответствующие представления формул f1 и f2. На рис. 9.2 показано дерево-формула, соответствующее формуле (5*(3+8)). Создать и продемонстрировать работу программы, которая вычисляет (как целое число) значение дерева-формулы Т.
13. Создать и продемонстрировать работу программы, которая по формуле (см. упр.12) из текстового файла f строит соответствующее дерево-формулу Т. 14. Создать и продемонстрировать работу программы, которая печатает дерево-формулу Т (см. упр.12) в виде соответствующей формулы. 15. Создать и продемонстрировать работу программы, которая проверяет, является ли двоичное дерево Т деревом-формулой (см. упр.12). 16. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f +1), (0+ f), (f -0), (f *1) и (1* f), на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f *0) и (0* f), - на вершину с 0. 17. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)). 18. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)) на поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)). 19. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая строит дерево-формулу Т1 - производную дерева-формулы Т по переменной, однобуквенное имя которой является значением литерного параметра v. 20. Предложить и описать на Паскале представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая вычисляет (как целое число) значение дерева-формулы Т. 21. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая по формуле из текстового файла f строит соответствующее дерево-формулу Т. 22. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая печатает дерево-формулу Т в виде соответствующей формулы. 23. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая проверяет, является ли двоичное дерево Т деревом-формулой. 24. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f+1), (0+f), (f-0), (f*1) и (1*f), на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f), - на вершину с 0. 25. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)). 26. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)) на поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)). 27. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая строит дерево-формулу Т1 - производную дерева-формулы Т по переменной, однобуквенное имя которой является значением литерного параметра v. 28. Деревом поиска, или таблицей в виде дерева, называется двоичное дерево, в котором слева от любой вершины находятся вершины с элементами, меньшими элемента из этой вершины, а справа - с большими элементами (предполагается, что все элементы дерева попарно различны и что их тип (ТЭД) допускает применение операций сравнения). Пример такого дерева показан на рис. 9.2. Описав тип дерево (см. выше) и тип файл: type файл=file of ТЭД; написать и продемонстрировать программу, которая проверяет, входит ли элемент Е в дерево поиска Т. 29. Тип дерево и тип файл, такие же, как в упр 28. Написать и продемонстрировать программу, которая записывает в файл f элементы дерева поиска Т в порядке их возрастания. 30. Тип дерево и тип файл, такие же как в упр 28. Написать и продемонстрировать программу, которая добавляет к дереву поиска Т новый элемент Е, если его не было в Т. 31. Тип дерево и тип файл, такие же как в упр 28. Написать и продемонстрировать программу, которая по файлу f, все элементы которого различны, строит соответствующее дерево поиска Т. 32. Во внешнем текстовом файле PROG записана (без ошибок) некоторая программа на языке Паскаль. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и/или цифр. Напечатать в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождений в текст программы. (Учесть, что в идентификаторах одноименные прописные и строчные буквы отождествляются, что внутри литерных значений, строк-констант и комментариев последовательности из букв и цифр не являются идентификаторами и что в записи вещественных чисел может встречаться буква Е или е). Для хранения идентификаторов использовать дерево поиска, элементами которого являются пары - идентификатор и число его вхождений в текст программы. 33. Решить предыдущую задачу, но вместе с каждым идентификатором печатать в возрастающем порядке номера всех строк текста программы, в которых он встречается. 34. Решить задачу 32 при условии, что максимальная длина идентификаторов заранее не известна. 35. Решить задачу 33 при условии, что максимальная длина идентификаторов заранее не известна. E.2.8. Литература по теме «Структуры данных» 1. Берзтисс А.Т. Структуры данных. - М.: Статистика, 1974. 2. Трамбле Ж., Соренсон П. Введение в структуры данных. - М.: Машиностроение, 1982. 3. Вирт Н. Алгоритмы + структуры данных = программы. - М.: Мир, 1985. 4. Костин А.Е., Шаньгин В.Ф. Организация и обработка структур данных в вычислительных системах. - М.: Высшая школа, 1987. 5. Липский В. Комбинаторика для программистов. – М.: Мир, 1988. 6. Абрамов С.А. и др. Задачи по программированию. – М.: Наука, 1988. 7. Вирт Н. Алгоритмы и структуры данных. - М.: Мир, 1989. 8. Иенсон К., Вирт Н. Паскаль. Руководство для пользователя. - М.: Финансы и статистика, 1989. 9. Пильщиков В.С. Сборник упражнений по языку Паскаль: Учеб. пособие для вузов. - М.: Наука, 1989. 10. Попов А.А. Программирование в среде СУБД FoxPro 2.0. – М.: Радио и связь, 1994. 11. Воробович Н.П. Введение в структуры данных. - Красноярск: СТИ, 1994.
|

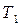 и
и 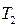 обозначают деревья, а Е – величину типа ТЭД.
обозначают деревья, а Е – величину типа ТЭД.




