E.2.6. Очереди, стеки, деревья
1. Для работы с очередью, т.е. последовательностью элементов, в которую элементы всегда добавляются в конец, а удаляются из начала ("первым пришел - первым ушел"), нужны обычно следующие операции: ОЧИСТОЧ(Q) - создать пустую очередь Q (очистить очередь); ПУСТОЧ(Q) - проверить, является ли очередь Q пустой; ПЕЧОЧ(Q) – распечатать содержимое очереди; ВОЧЕРЕДЬ(Q,x) - добавить в конец очереди Q элемент x; ИЗОЧЕРЕДЬ(Q,x) - удалить из очереди Q первый элемент, присвоив его параметру x. Требуется для каждого из указанных ниже представлений очереди описать соответствующий тип ОЧЕРЕДЬ, считая, что все элементы очереди имеют некоторый тип ТЭО, и реализовать в виде процедур или функций перечисленные операции над очередью (если операция по тем или иным причинам не может быть выполнена, следует передать управление некоторой процедуре ОШИБКА(k), считая ее уже описанной, где k - номер ошибки: 1 - переполнение очереди, 2 - исчерпание очереди). Представление очереди (n – целая константа >1): а) для каждой очереди отводится свой массив из N компонентов типа ТЭО, в котором элементы очереди занимают группу соседних компонент, индексы первой и последней из которых запоминаются; при этом, когда очередь достигает правого края массива, все ее элементы сдвигаются к левому краю; б) аналогичное представление, но массив как бы склеивается в кольцо, поэтому если очередь достигает правого края массива, то новые элементы записываются в начало массива; в) для каждой очереди создается свой однонаправленный список из элементов типа ТЭО, при этом запоминаются ссылки на первое и последнее звенья списка. 2. Для работы со стеком, т.е. последовательностью элементов, в которой элементы всегда добавляются в конец и удаляются из конца ("последним пришел - первым ушел"), нужны обычно следующие операции: ОЧИСТЕК(S) - создать пустой стек S (очистить стек); ПЕЧСТЕК(S) – распечатать содержимое стека; ПУСТЕК(S) - проверить, является ли стек S пустым; ВСТЕК(S,X) - добавить в конец стека S элемент X; ИЗСТЕК(S,X) - удалить из очереди S последний элемент, присвоив его параметру X. Требуется для каждого из указанных ниже представлений стека описать соответствующий тип СТЕК, считая, что все элементы стека имеют некоторый тип ТЭC, и реализовать в виде процедур или функций перечисленные операции над стеком (если операция по тем или иным причинам невыполнима, следует передать управление некоторой процедуре ОШИБКА(k), считая ее уже описанной, где k - номер ошибки: 1 -переполнение стека, 2 -исчерпание стека). Представление стека (n -целая константа>1): а) для каждого стека отводится свой массив из n компонентов типа ТЭC, в начале которого располагаются элементы стека, при этом запоминается индекс компоненты массива, занятой последним элементом стека; б) для каждого стека создается свой однонаправленный список, в котором элементы стека располагаются в обратном порядке. 3. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1)), решить следующую задачу. За один просмотр файла f и без использования дополнительных файлов напечатать элементы файла f в следующем порядке: сначала - все числа, меньшие A, затем - все числа из отрезка [ A,B ] (где A<B), и, наконец, - все остальные числа, сохраняя исходный взаимный порядок в каждой из этих трех групп чисел. 4. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1))), решить следующую задачу. Содержимое текстового файла f, разделенное на строки, переписать в текстовый файл g, перенося при этом в конец каждой строки все входящие в нее цифры (с сохранением исходного взаимного порядка как среди цифр, так и среди остальных литер строки). 5. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1))), решить следующую задачу. type имя= (Анна,..., Яков); дети= array [имя,имя] of boolen; потомки=file of имя; Считая заданными имя И и массив Д типа ДЕТИ(Д[X,Y]=true, если человек по имени Y является ребенком человека по имени X), записать в файл P типа ПОТОМКИ имена всех потомков человека с именем И в следующем порядке: сначала - имена всех его детей, затем - всех его внуков, затем - всех правнуков и т.д.. 6. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК(S), ПЕЧСТЕК(S), ОЧИСТЕК(S), ВСТЕК(S,x) и ИЗТЕК(S,x) (задача 2)), решить следующую задачу. Напечатать содержимое текстового файла t, выписывая литеры каждой его строки в обратном порядке. 7. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК(S), ПЕЧСТЕК(S), ОЧИСТЕК(S), ВСТЕК(S,x) и ИЗТЕК(S,x) (задача 2))), решить следующую задачу. Проверить, является ли содержимое текстового файла t правильной записью формулы следующего вида: <формула>::= <терм> ï <терм>+<формула> ï <терм>-<формула> <терм>::= <имя> ï <(<формула>) ï [<формула>] ï {<формула>} <имя::= x ï y ï z 8. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК(S), ПЕЧСТЕК(S), ОЧИСТЕК(S), ВСТЕК(S,x) и ИЗТЕК(S,x) (задача 2)), решить следующую задачу. В текстовом файле f записана без ошибок формула следующего вида: <формула>::= <цифра>ï М (<формула>,<формула>)ï м (<формула>,<формула>) <цифра>::= 0 ï 1 ï 2 ï 3 ï 4 ï 5 ï 6 ï 7 ï 8 ï 9, где М обозначает функцию max, а м обозначает функцию min. Вычислить (как целое число) значение данной формулы (например, М (5, м (6, 8))® 6). 9. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК(S), ПЕЧСТЕК(S), ОЧИСТЕК(S), ВСТЕК(S,x) и ИЗТЕК(S,x) (задача 2)), решить следующую задачу. В текстовом файле LOG записано без ошибок логическое выражение (ЛВ) в следующей форме: <ЛВ>::=true ï false ï (ù <ЛВ>) ï (<ЛВ> Ù <ЛВ> ï (<ЛВ> È <ЛВ>), где знаки ù, Ù и È обозначают соответственно отрицание, коньюнкцию и дизьюнкцию. Вычислить (как boolean) значение этого выражения. 10. Используя очередь и/или стек (предварительно выбрав и описав их типы и создав все нужные для решения функции и процедуры для работы над ними (задача 1 и/или 2)), решить следующую задачу. В текстовом файле f записан текст, сбалансированный по круглым скобкам: <текст>::=<пусто> ï <элемент><текст>; <элемент>::=<буква> ï (<текст>) Требуется для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров в порядке возрастания номеров позиций закрывающих скобок. Например, для текста A+(45-f(X)*(B-C)) надо напечатать: 8 10; 12 16; 3 17. 11. Используя очередь и/или стек (предварительно выбрав и описав их типы и создав все нужные для решения функции и процедуры для работы над ними (задача 1 и/или 2)), решить следующую задачу. В текстовом файле f записан текст, сбалансированный по круглым скобкам: <текст>::=<пусто> ï <элемент><текст>; <элемент>::=<буква> ï (<текст>) Требуется для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров в порядке возрастания номеров позиций открывающих скобок. Например, для текста A+(45-f(X)*(B-C)) надо напечатать 3 17; 8 10; 12 16. 12. Под "выражением" будем понимать конструкцию следующего вида: <выражение>::=<терм> ï <терм><терм><знак><выражение> <знак+->::=+ ï - <терм>::=<множитель> ï <множитель>*<терм> <множитель>::=<число>ï<переменная>ï(<выражение>)ï<множитель>**<число> <число>::=<цифра> <переменная>::=<буква>, где ** обозначают возведение в степень. Постфиксной формой записи выражения a Ñ b называется запись, в которой знак операции размещен за операндами: ab Ñ. Примеры: a-b ® ab- a*b+c ® ab*c- (т.е. (ab*)c+) a*(b+c) ® abc+* (т.е. a(bc+)*) a+b**c**d*e ® abc**d**e*+ Описать функцию value(postfix), которая вычисляет как целое число значение выражения (без переменных), записанного в постфиксной форме в текстовом файле postfix. Использовать следующий алгоритм вычисления. Выражение просматривается слева направо. Если встречается операнд (число), то его значение (как целое) заносится в стек, а если встречается знак операции, то из стека извлекаются два последних элемента (это операнды данной операции), над ними выполняется операция и ее результат записывается в стек. В конце концов в стеке останется только одно число - значение всего выражения. 13. Описать процедуру translate(infix,postfix), которая переводит выражение (определение "выражения" смотри в задаче 12), записанное в обычной (инфиксной) форме в текстовом файле infix, в постфиксную форму и в таком виде записывает его в текcтовый файл postfix. Использовать следующий алгоритм перевода. В стек записывается открывающая скобка, и выражение просматривается слева направо. Если встречается операнд (число или переменная), то он сразу переносится в файл postfix. Если встречается открывающая скобка, то она заносится в стек, а если встречается закрывающая скобка, то из стека извлекаются находящиеся там знаки операций до ближайшей открывающей скобки, которая также удаляется из стека, и все знаки (в порядке их извлечения) записываются в файл postfix. Когда же встречается знак операции, то из конца стека извлекаются (до ближайшей скобки, которая сохраняется в стеке) знаки операций, старшинство которых больше или равно старшинству данной операции, и они записываются в файл postfix, после чего рассматриваемый знак заносится в стек. В заключение выполняются такие же действия, как если бы встречалась закрывающая скобка. 14. Описать (нерекурсивную) процедуру infixprint(postfix), которая печатает в обычной (инфиксной) форме выражение (определение "выражения" смотри в задаче 12), записанное в постфиксной форме в текстовом файле postfix (лишние скобки желательно не печатать). 15. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все символы, отличные от цифр, а затем все цифры, сохраняя исходный порядок в каждой из этих групп символов. 16. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать сначала все гласные буквы, затем знаки препинания и, наконец, - все согласные, сохраняя исходный порядок в каждой из этих групп символов. 17. В текстовом файле записана без ошибок формула вида: цифра или R (формула, формула), или L (формула, формула), где R обозначает функцию взять правое число, L -взять левое число. Вычислить значение данной формулы (например, R(8, R(3,L(4,5)))=4). 18. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все однозначные числа, затем двузначные, сохраняя исходный порядок чисел в каждой из этих групп. 19. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла напечатать элементы файла в следующем порядке: сначала все символы, отличные от знаков препинания и цифр, затем знаки препинания и наконец – все цифры, сохраняя исходный порядок в каждой из этих групп символов. 20. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла напечатать элементы файла в следующем порядке: сначала все числа, делящиеся на 5, затем все нечетные числа, не делящиеся на 5, и наконец – все четные числа, не делящиеся на 5, сохраняя исходный порядок в каждой из этих групп чисел. 21. В текстовом файле записана без ошибок формула вида: цифра или s (формула, формула) или p (формула, формула), где s (a,b) = (a+b) mod 10, p (a,b) = (a*b) mod 10. Вычислить значение этой формулы. Например, p (6, s (8, 4)) = 2. 22. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все однозначные числа, затем все двузначные. Первая группа чисел выводится в исходном порядке, вторая - в обратном порядке. Например: 2, 15, 7, 24, 37, 8 ® 2, 7, 8, 37, 24, 15. 23. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все знаки препинания в исходном порядке, затем все согласные в обратном порядке, затем все согласные в обратном порядке, и наконец – все гласные в исходном порядке. 24. В текстовом файле записана без ошибок формула вида: цифра или m (формула, формула) или p (формула, формула), где m (a, b) = (a-b) mod 10, p (a, b) = (a+b) mod 10. Вычислить значение этой формулы. Например, m (9, p (p (3, 5), m (3, 8))) = 6. В упражнениях 25-33 использовать двоичные деревья при следующем их описании. type ТЭД=...: {тип элементов дерева} дерево= ^ вершина; вершина=record элем:ТЭД; лев, прав:дерево end; В этих упражнениях Т, 25. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая присваивает параметру Е элемент из самого левого листа непустого дерева Т (лист - вершина, из которого не выходит ни одной ветви). Продемонстрировать работу программы. 26. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая определяет число вхождений элемента Е в дерево Т. Продемонстрировать работу программы. 27. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая вычисляет среднее арифметическое всех элементов непустого дерева Т (ТЭД=real). Продемонстрировать работу программы. 28. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая заменяет в дереве Т все отрицательные элементы на их абсолютные величины (ТЭД=real). Продемонстрировать работу программы. 29. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая меняет местами максимальный и минимальный элементы непустого дерева Т, все элементы которого различны (ТЭД=real). Продемонстрировать работу программы. 30. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая печатает элементы из всех листьев дерева Т (ТЭД=char). Продемонстрировать работу программы. 31. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая печатает все элементы дерева Т по уровням (сначала - из корня дерева, затем (слева направо) - из вершин, дочерних по отношению к корню, затем (также слева направо) - из вершин, дочерних по отношению к этим вершинам, и т.д.) (ТЭД=integer). Продемонстрировать работу программы. 32. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая находит в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с элементом Е; если Е не входит в Т, за ответ принять -1. Продемонстрировать работу программы. 33. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая подсчитывает число вершин на n -ом уровне непустого дерева Т (корень считать вершиной 0-го уровня). Продемонстрировать работу программы.
|

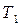 и
и 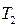 обозначают деревья, а Е – величину типа ТЭД.
обозначают деревья, а Е – величину типа ТЭД.


