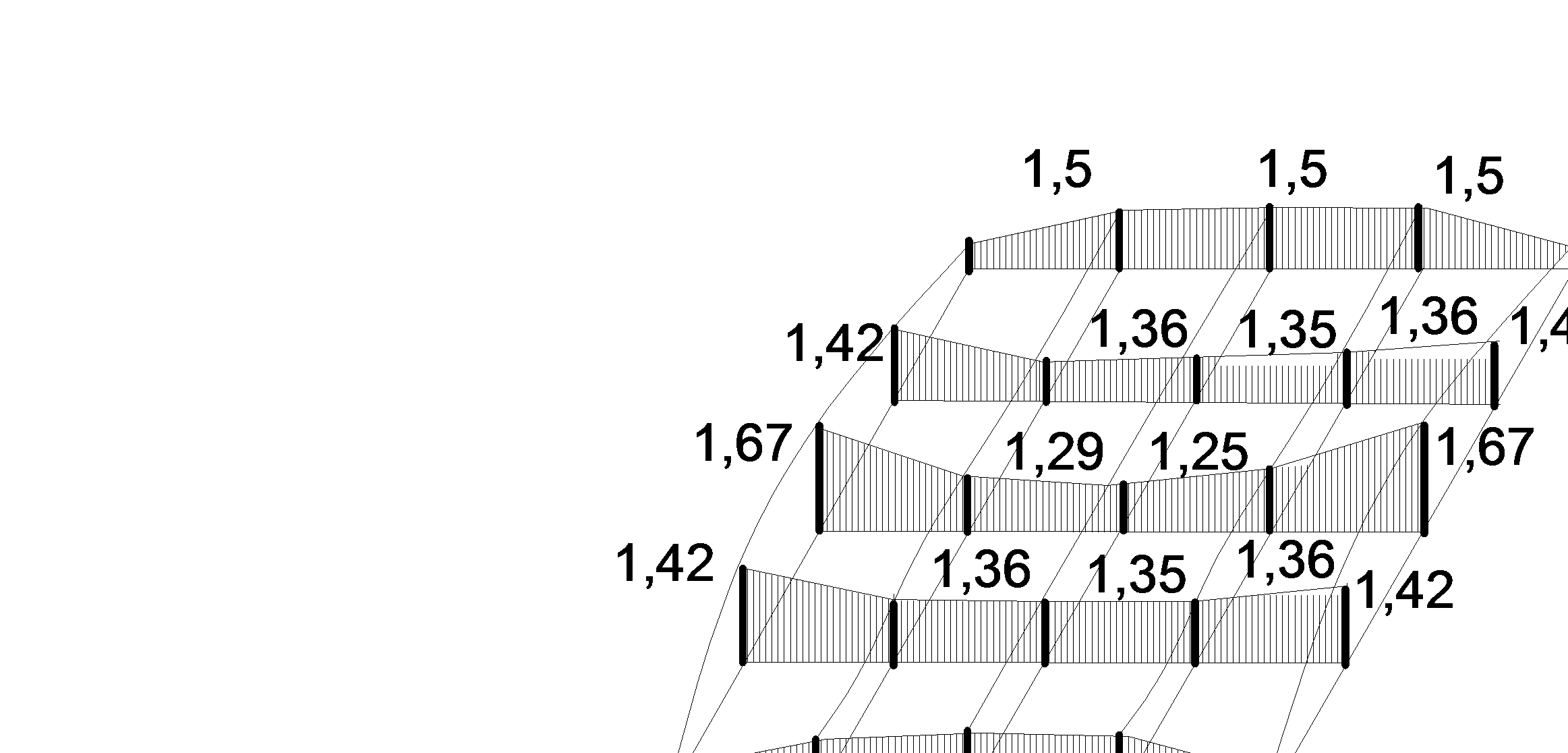
После подстановки значений функции φ; для контурных и законтурных точек система уравнений принимает вид:
20φ0- 16φ1-16φ2+8φ3- 4 = 0;
-8φ0+22φ1+4φ2-16φ3+36 =0;
-8φ0 + 4φ1 + 22φ2 -16φ3 + 40 = 0;
2φ0 - 8φ1 - 8φ2 + 24φ3 + 20 = 0;
Для решения системы уравнений используем стандартные программы.
Решение системы: φ0=-10,16; φ1=-7,65; φ2=-7,88; φ3=-5,16.
Для проверки правильности необходимо подставить значения φi в каждое из уравнений системы.
5. Определяем напряжения в точках пластины
σx = d 2φ/dу2 =1/λ2 (φi,j-1-2φi,j+ φi,j+1)=1/λ2
σy= d 2φ/dx2 =1/ /λ2 (φi-1,j-2φi,j+ φi+1,j)=
1/ /λ2
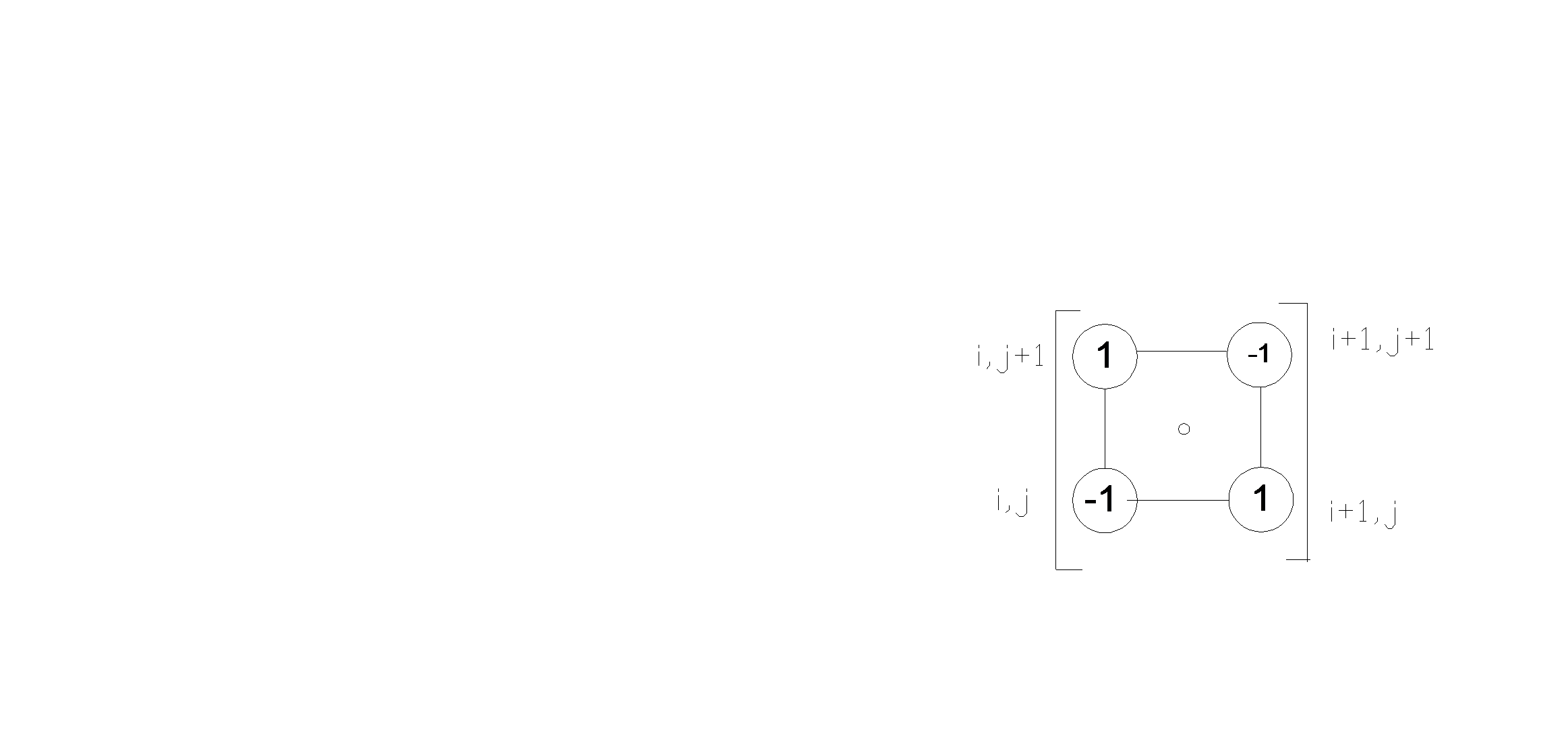
Напряжения σx, σy определяются по формулам (1) в узлах сетки. Напряжения τхy (по формуле (2)) при редкой сетке (как у нас) целесообразно определять для точек,расположенных в центрах тяжести площадок (точки А,Б,В,Г,Д,Е и т.д.) рис.5.

| σx (кН/м2)
| σу (кН/м2)
|
| № точки
| Конечно-разностное выражение
| Величина напряже-
ния
| № точки
| Конечно-разност-ное выражение
| Величина напряже-ния
|
| σx(0)
| 1/λ2(φ2-2φ0+ φ2)
| 1,14
| σу(0)
| 1/λ2(φ1-2φ0+ φ1)
| 1,25
|
| σx(1)
| 1/λ2(2φ3-2φ1)
| 1,24
| σу(1)
| 1/λ2(φд-2φ1+ φ0)
| 1,29
|
| σx(2)
| 1/λ2(φа-2φ2+ φ0)
| 0,9
| σу(2)
| 1/λ2(φ3-2φ2+ φ3)
| 1,35
|
| σx(3)
| 1/λ2(φб-2φ3+ φ1)
| 0,92
| σу(3)
| 1/λ2(φг-2φ3+ φ2)
| 1,36
|
| σx(а)
| 1/λ2(φа1-2φа+ φ2)
| 0,56
| σу(а)
| 1/λ2(φб-2φа+ φб)
| 1,5
|
| σx(б)
| 1/λ2(φб1-2φб+ φд)
| 0,42
| σу(б)
| 1/λ2(φв-2φб+ φа)
| 1,5
|
| σx(в)
| 1/λ2(φв1-2φв+ φг)
|
| σу(в)
| 1/λ2(φв2-2φв+ φб)
| 1,0
|
| σx(г)
| 1/λ2(φв-2φг+ φд)
| 1,0
| σу(г)
| 1/λ2(φг1-2φг+ φ3)
| 1,42
|
| σx(д)
| 1/λ2(φг-2φд+ φг)
| 1,5
| σу(д)
| 1/λ2(φд1-2φд+ φ1)
| 1,67
|
| τxy (кН/м2)
|
| № точки
| Конечно-разностное выражение
| Величина напряжения
|
| τxy (А)
| 1/λ2(φв+ φ3- φб - φг)
| 0,21
|
| τxy (Б)
| 1/λ2(φб+ φ2- φа - φ3)
| 0,07
|
| τxy (В)
| 1/λ2(φа+ φ3- φб - φг)
| -0,07
|
| τxy (Г)
| 1/λ2(-φв- φ3+ φб + φг)
| -0,21
|
| τxy (Д)
| 1/λ2(φг+ φ1- φд – φ3)
| 0,13
|
| τxy (Е)
| 1/λ2(-φ1- φ2+ φ3 + φ0)
| 0,05
|
| τxy (Ж)
| 1/λ2(φ2+ φ1- φ3 φ0)
| -0,05
|
6. Построение эпюр напряжений σx,σy,τхy
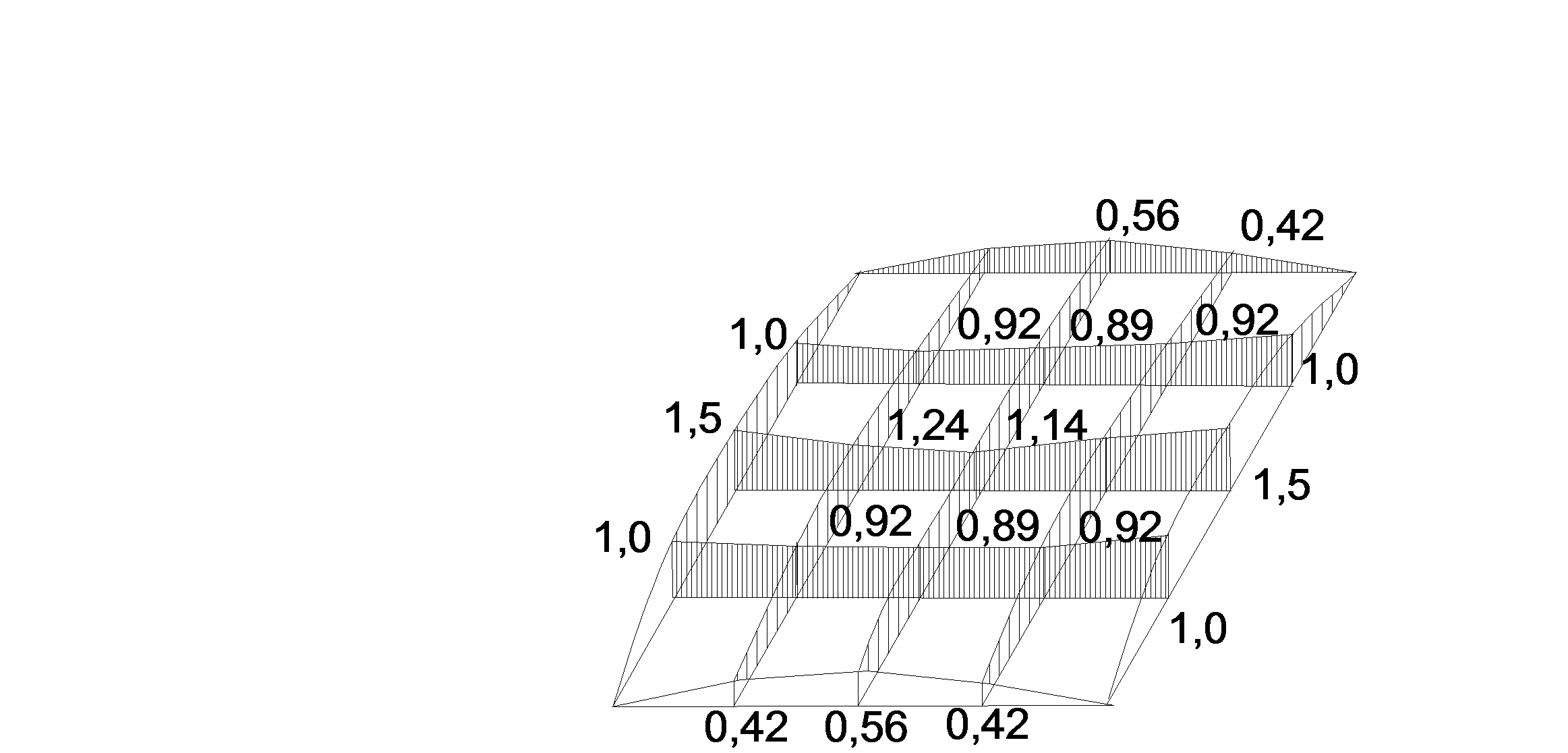
.