В РЕЖИМЕ КОМАНДНОЙ СТРОКИ

Лабораторная работа № 4

по дисциплине:

Прикладные нечёткие системы

на тему:

ЭКСТРАКЦИЯ НЕЧЁТКОЙ СИСТЕМЫ

В РЕЖИМЕ КОМАНДНОЙ СТРОКИ

 

Выполнил:

студент группы ВТМ-11

Соколов И.П.

Проверил:

доцент Боцула Л.Н.

 

 

2012 г.

Задание: Произвести двухэтапную процедуру проектирования нечёткой системы типа Сугено: на первом этапе синтезировать нечёткие правила из экспериментальных данных с использованием субтрактивной кластеризации; на втором этапе настроить параметры нечёткой модели с помощью ANFIS-алгоритма. Изложить на примере построения нечёткой системы, моделирующей зависимость числа пригородных автомобильных поездок (y) от следующих демографических показателей: количество жителей (х1); количество автомобилей (х3); средний уровень доходов на один дом (х4); уровень занятости населения (х5).

Выполнение:

1) Для загрузки данных напечатаем команду tripdata, по которой в рабочей области создаётся обучающая выборка из 75 пар данных «входы-выходы» (переменные datin и datout) и тестовая выборка из 25 данных (переменные chkdatin и chkdatout) (рис.1). Экспериментальные данные собраны из 100 транспортных зон округа Ньюкасл.

рис.1

2) На рис.2 приведена обучающая выборка в виде однофакторных зависимостей «входы-выход». Рисунок построен следующими командами:

for i=1:5

subplot(3,5,i)

plot(datin(:,1), datout, 'kx')

xlabel(['x_' num2str(i)])

ylabel('y');

end

рис.2

 

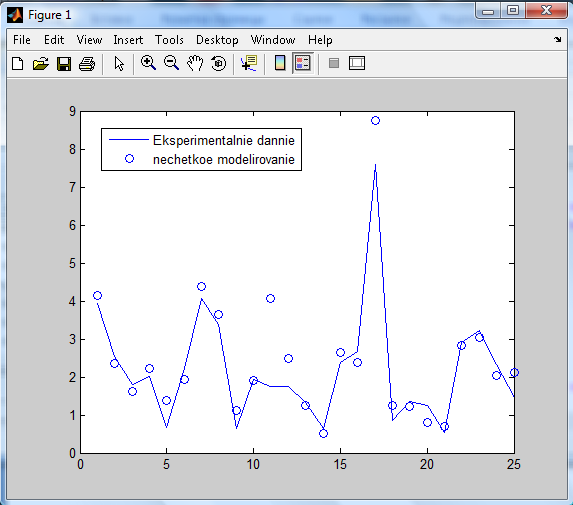
3) С помощью функции genfis2 синтезируем из данных нечёткую модель Сугено с использованием субтрактивного метода кластеризации. Это быстрый одноходный метод без итерационных процедур оптимизации. При вызове этой функции необходимо указать радиусы кластеров, которые определяют, как далеко от центра кластера могут находиться его элементы. Значения радиусов должны быть из диапазона [0,1]. Как правило, хорошие нечёткие базы знаний получаются, когда радиусы находятся в диапазоне [0.2, 0.5]. Радиусы кластеров задаются третьим аргументом функции. Будем считать, что координаты являются равноважными, поэтому значение этого аргумента можно задать скаляром. Следующая команда вызывает функцию genfis2 при значении радиусов кластера, равных 0.5:

fis=genfis2(datin, datout, 0.5)

В результате синтезируется нечёткая модель Сугено первого порядка с тремя правилами.

fis =

name: 'sug51'

type: 'sugeno'

andMethod: 'prod'

orMethod: 'probor'

impMethod: 'min'

aggMethod: 'max'

defuzzMethod: 'wtaver'

input: [1x5 struct]

output: [1x1 struct]

rule: [1x3 struct]

4) Для вычисления ошибки моделирования на обучающей выборке вызовем следующие команды:

fuzout=evalfis(datin, fis);

trnRMSE=norm(fuzout-datout)/sqrt(length(fuzout))

В результате получим, что значение невязки равно:

trnRMSE =

0.5276

5) Теперь проверим, как работает модель вне точек обучения, т.е. на тестовой выборке. Для этого выполним следующие команды:

chkfuzout=evalfis(chkdatin,fis);

chkRMSE=norm(chkfuzout-chkdatout)/sqrt(length(chkfuzout))

Значение ошибки на тестовой выборке равно:

chkRMSE =

0.6179

Видно, что ошибка на тестовой выборке больше, чем на обучающей. Сравним экспериментальные данные из тестовой выборки с результатами нечёткого моделирования, применяя такие команды:

>> plot(chkdatout)

>> hold on

>> plot(chkfuzout, 'o')

>> hold off

>> legend('Eksperimentalnie dannie','nechetkoe modelirovanie')

Результаты представлены на рис.3. Видно, что нечёткая модель описывает тенденцию в данных. Однако в отдельных случаях расхождения между экспериментальными данными и результатами моделирования значительные.

 

рис.3

6) Попытаемся улучшить модель с помощью ANFIS-обучения. Зададим относительное небольшое количество итераций обучения – 50. Для обучения будем использовать только обучающую выборку с последующей проверкой настроенной нечёткой модели на тестовой выборке. Обучение осуществим командой:

fis2=anfis([datin datout], fis, [50 0 0,1])

7) Рассчитаем ошибки моделирования на обучающей и тестовой выборках после обучения:

fuzout2=evalfis(datin,fis2);

trnRMSE=norm(fuzout2-datout)/sqrt(length(fuzout2))

trnRMSE =

0.5276

chkfuzout2=evalfis(chkdatin,fis2);

chkRMSE=norm(chkfuzout2-chkdatout)/sqrt(length(chkfuzout2))

chkRMSE =

0.6179

Значения ошибок равны: trnRMSE = 0.5276 и chkRMSE = 0.6179. Возросло качество моделирования на обучающей выборке. Адекватность модели на тестовой выборке улучшилась несущественно. На это указывает график (рис.4), построенный командами:

>> plot(chkdatout)

>> hold on

>> plot(chkfuzout2, 'o')

>> legend('Eksperimentalnie dannie','nechetkoe modelirovanie')

>> hold off

Исследуем, как зависит адекватность нечёткой модели от длительности обучения. Для этого вызовём функции anfis в следующем формате:

[fis3,trnErr,stepSize,fis4,chkErr]=anfis([datin datout],fis,[200 0 0.1],[],[chkdatin chkdatout])

Третий входной аргумент этой функции задаёт 200 итераций. После 200 итераций алгоритма минимальные ошибки на обучающей и тестовой выборках равны 0,3266 и 0,5830 соответственно.

8) Посмотрим, на каких итерациях алгоритма обучения получены модели с минимальными ошибками. Для этого выведем кривые обучения с помощью команд:

>> plot(1:200, trnErr, '.k-', 1:200, chkErr, 'b-');

>> legend ('Oshibka na tekuschey viborke','Oshibka na testovoy viborke');

>> xlabel('Iteracii algoritma obucheniya');

>> ylabel('RMSE')

рис.4

Динамика обучения (рис.4) показывает, что ошибка на тестовой выборке имеет тенденцию к уменьшению на протяжении около 50 итераций и достигает наименьшего значения на 52 итерации алгоритма обучения. Начиная с 52-й итерации проявляется эффект переобучения, состоящий в потере генерализирующих свойств модели. Вне точек обучения адекватность модели низкая – результаты моделирования сильно отличаются от экспериментальных данных. Для предотвращения переобучения обычно использует тактику «раннего останова» - прекращение обучения при возрастании ошибки на тестовой выборке.