Условия немедленной несостоятельности биметаллизма

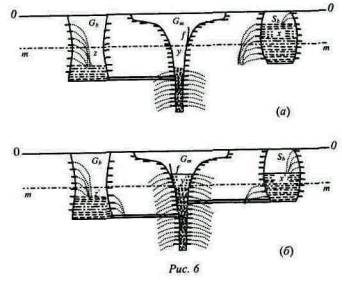
Очевидное действие закона Грешема состоит в понижении покупательной силы денег при всяком удобном случае. Ис тория мирового денежного обращения в значительной мере представляет собой перечень примеров порчи денег, часто по повелению государей. Наша главная задача в настоящий момент заключается при рассмотрении закона Грешема в более полной формулировке причин, определяющих покупательную силу денег при денежных системах, подверженных действию закона Грешема. Начнем с биметаллизма.

Чтобы вполне понять влияние какой-либо монетной системы на покупательную силу денег, мы сначала должны понять, как система действует [Fisher I. The Mechanics of Bimetallism (British) // Economic Journal. 1894. September. P. 527-536.]. Было много возражений, что биметаллизм когда-нибудь действовал или мог действовать, потому что дешевый металл должен был вытеснять более дорогой. Нашей первой задачей является показать, совершенно независимо от желательности этого, что биметаллизм может действовать и действует при известных условиях, но не при других. Чтобы выяснить, когда он будет действовать и когда не будет, мы будем продолжать пользоваться механической иллюстрацией [В настоящем приложении она до некоторой степени подобна символу, на который намекает Джевонс в его “Money and the Mechanism of Exchange”. New York (Appleton), 1896.P.140.] последней главы, в которой сумма золотых слитков представлена содержимым сосуда G_b (рис. 6, 7). Здесь, как и прежде, мы изображаем покупательную силу, или ценность, золота расстоянием между уровнем жидкости и линией 00. В последней главе наш рисунок представлял только один металл - золото, но представлял этот металл в двух сосудах: в сосуде слитков и в сосуде монет. Теперь мы несколько видоизменим этот рисунок. Во-первых, как на рис. 6а, мы прибавим сосуд для серебряных слитков S_b, который будет несколько иной формы и размера, чем сосуд G_b. Этот сосуд может быть использован для того, чтобы показать отношение между ценностью, или покупательной силой, серебра и его количеством в изделиях и слитках. Здесь, следовательно, мы имеем три сосуда. Сначала серебро совершенно изолировано, но потом мы соединим сосуд с серебром со средним сосудом. Сначала предположим, что средний сосуд, который содержит деньги, исключительно наполнен только золотыми монетами (рис. 6а), а серебро совсем не употребляется как деньги. Другими словами, денежная система совершенно та же, которую мы рассматривали в предыдущей главе. Единственное изменение, которое мы вводим в этот рисунок, состоит в прибавлении другого сосуда S_b, совершенно оторванного, указывающего количество и ценность серебряных слитков.

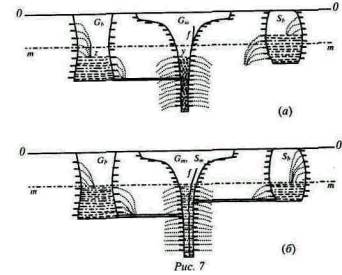
Дальше предположим, что справа открыта трубка, соединяющая сосуд S_b с денежным сосудом, т. е. мы вводим биметаллизм. При биметаллизме правительства открывают свои монетные дворы для свободной чеканки обоих металлов в фиксированном отношении, т. е. в фиксированном отношении между ценностями обоих названных металлов. Например, если серебряный доллар содержит 16 долей серебра на каждую долю золота в золотом долларе, отношение выразится в 16:1. При такой системе должник может выбирать, если он иным путем не связан своим контрактом, уплату или золотыми или серебряными деньгами. Эти два условия действительно являются двумя необходимыми реквизитами полного биметаллизма, а именно: во-первых, свободная и неограниченная чеканка обоих металлов в фиксированном соотношении и, во-вторых, неограниченная законная платежная сила обоих металлов в том же соотношении. Эти новые условия изображены на рис. 6б (и позднее на рис. 76), где трубка дает доступ серебру в денежный, или центральный, сосуд [Конечно, одна частица жидкости, наполняющей центральный сосуд, представляет соединение золота и серебра в их чеканных весовых пропорциях. Если соотношение между металлами установлено как 16:1, сосуды должны быть устроены так, чтобы один кубический дюйм жидкости представлял собой 1 унцию золота или 16 унций серебра и чтобы число дюймов, отделяющих поверхности жидкостей от линии 00, представляло бы предельную полезность 1 унции золота и 16 унций серебра соответственно.].

То, что мы хотим изобразить, не есть соотношение между количествами добычи из рудников, слитков и изделий из обоих металлов, но соотношение между слитками и монетами из обоих металлов. Мы можем, следовательно, не обращать в настоящий момент внимания на все входы и выходы из сосудов, за исключением сообщения между сосудом слитков и сосудом монет.

Теперь в этих сосудах расстояние от поверхности жидкости до линии 00, как мы уже сказали, представляет покупательную силу золота и серебра. Но каждая единица серебра (т. е. каждая капля жидкости, изображающей серебро, как в монетах, так и в слитках) содержит в 16 раз больше частиц, чем каждая единица золота (т. е. каждая капля жидкости, изображающей золото, как в монетах, так и в слитках). Это значит, что одна единица жидкости изображает или один золотой, или один серебряный доллар. Мы хотим изобразить только относительную покупательную силу соответственных единиц.

Жидкости, представляющие золотые и серебряные деньги, разделены подвижной перепонкой f. На рис. 6а эта перепонка находится у правой стенки сосуда, на рис. 6б-у левой стенки, на рис. 7а - опять у правой стенки, а на рис. 7б - посередине. Рисунки а представляют положение до открытия монетных дворов для свободной чеканки серебра. Рисунки б представляют положение после этого открытия и когда закон Грешема начинает действовать. Если перед самым введением биметаллизма уровень серебра в сосуде S_b ниже уровня золота в сосуде G_b, то закон, вводящий биметаллизм, не окажет никакого влияния, т.е. серебряные слитки не потекут в денежный сосуд, так как жидкости вообще не текут вверх; но если, как мы видим на рис. 6а или 7а, уровень серебра выше, чем уровень золота, то, как только монетные дворы будут открыты для свободной чеканки серебра, оно потечет в обращение. Будучи сначала дешевле золота, серебро вытолкнет золотые деньги через левую трубку (т.е. путем переплавки монет) на рынок слитков. Это вытеснение золота может быть полным, как указано на рис. 6б, или только частичным, как указано на рис. 7б. Вытеснение будет продолжаться только до тех пор, пока не появится премия на золото, т. е. пока уровень серебра в сосуде слитков будет оставаться выше уровня золота в денежном сосуде или пока серебряные слитки будут дешевле золотых денег.

Предположим, что линия mm, как показано на рис. 6а, будет промежуточным уровнем, т.е. таким уровнем, что объем х, находящийся выше него, равняется сумме пустых объемов у и г, находящихся ниже этого уровня. Эта линия mm остается промежуточным уровнем, каково бы ни было распределение жидкостей между тремя сосудами. Как только с помощью трубки сообщение между сосудами будет установлено, серебро будет течь в денежный сосуд и, согласно закону Грешема, вытеснять золото.

Мы должны различать здесь два случая: 1) когда количество серебра х, находящееся выше промежуточной линии mm, превышает все содержимое денежного сосуда, расположенное ниже этой линии, 2) когда х меньше, чем содержимое денежного сосуда ниже названной линии. В первом случае очевидно, что серебро совершенно вытеснит золото из обращения, как указано в рис. 6б, где перепонка передвинулась от правой стенки к левой. Количество серебра в сосуде слитков будет меньше, чем прежде, а содержимое в сосуде золотых слитков будет больше, чем раньше.

Но это перераспределение есть только первый эффект, производимый открытием монетных дворов для свободной чеканки серебра. Нарушается равновесие между производством и потреблением как для золота, так и для серебра. Возросшая ценность серебра (так как уровень в S_b понизился) стимулирует производство, увеличивая разработку серебряных рудников (раскрытые входы справа), а с другой стороны, понизившаяся ценность золота (так как уровень в G_b повысился) понижает производство золота путем закрытия золотых рудников (закрытые входы слева). Подобные же изменения происходят и в отливах, т.е. в потреблении, трате и стирании каждого металла.

В результате оказывается, что получившиеся после первого перераспределения уровни не будут обязательно постоянными. Они могут возвратиться к первоначальному соотношению уровней, и при всех обычных условиях так и происходит. Но во всяком случае и это заслуживает особого внимания, они не могут вполне возвратиться к прежним уровням. Такое предположение было бы неосновательно, как показывает следующее рассуждение. Предположим на минуту, что серебро должно было бы вернуться к своему первоначальному уровню. Тогда приток серебра (производство) также вернулся бы к своему первоначальному размеру в зависимости от этого уровня, но отлив серебра (потребление, порча и т. д.) был бы больше, чем первоначально. Потребление в изделиях осталось бы прежним, но порча и потеря серебряных денег образовали бы дополнительный отлив. Тогда потребление (равное прежде производству) будет превышать производство и высокий первоначальный уровень не может быть удерживаем. Отсюда мы заключаем, что, каков бы ни был новый уровень перманентного равновесия, он будет лежать ниже старого уровня. Тот же самый аргумент, mutatis mutandis, доказывает, что для золота новый уровень перманентного равновесия будет лежать выше старого. Расстояние между двумя первоначальными уровнями будет тем самым уменьшено. Даже если бы биметаллизму не удалось установить совместного обращения обоих металлов и паритета цен, при данном соотношении в чеканке он привел бы в результате к понижению ценности более дорогого металла (золота) и к повышению таковой более дешевого (серебра). Такое действие взаимного приближения будет нами рассмотрено при обсуждении второго случая (в следующем параграфе).