Поправочные разницы

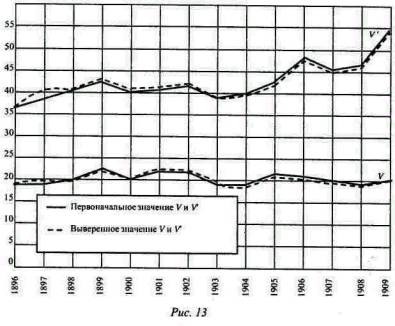
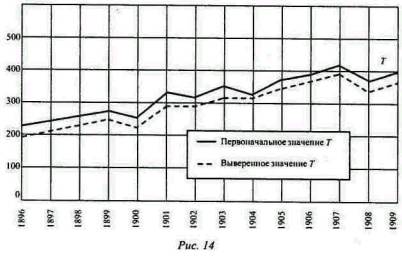
Теми, кто поверил априорному доказательству уравнения обмена, реальное значение замечательного совпадения в наших статистических выводах должно быть понято не как подтверждение правильности уравнения при помощи цифр, но, наоборот, как подтверждение правильности цифр при помощи уравнения. В нашей индуктивной проверке встречаются несовпадения, но все они не выходят за пределы погрешностей измерения. Эти несовпадения указывают, что в цифрах существуют незначительные ошибки, в противном случае эти цифры совершенно точно согласовывались бы с соотношением, указываемым уравнением обмена.

Нашей дальнейшей задачей является исследование этих неcовпадений и, насколько возможно, локализация встречающихся ошибок. Степень общей взаимной несогласованности между независимо вычисленными величинами лучше всего выражается степенью неравенства между вычисленными значениями величин (MV+M'V') и РТ, которые должны бы быть равны друг другу, т. е. РТ, деленное на (MV+M'V'), должно всегда равняться 1. Действительное деление дают цифры в столбце 2, озаглавленном “Первоначальное значение”, в следующей таблице. Столбец 3 будет объяснен ниже.

Вычисленное отношение РТ к (MV+M'V')

Цифры в столбце втором показывают, что вычисленные значения РТ бывают всегда больше, чем вычисленные значения MV+M'V', причем излишек колеблется от 24% до 0 при средней величине 11%.

Но эти расхождения между РТ и (MV+M'V') могут быть в значительной степени уменьшены одним только изменением основания измерения цен. Исходной величиной, которую мы до сих пор принимали, был уровень цен 1909 г. Но поскольку index numbers'ы имеют только относительные значения, мы считаем себя свободными в выборе другого ряда чисел, содержащего также относительные величины. В силу этой прерогативы мы решили уменьшить все числа для Р на 11%, т. е. на среднюю величину первоначального расхождения. Результатом является уменьшение РТ на 11%, и таким образом изменяется ряд расхождений, показанных в столбце 2, в (приблизительный) ряд чисел, показанных в столбце 3. Эти числа колеблются в пределах от 13% выше единицы и до 11% ниже единицы. Эти ошибки очень незначительны, фактически гораздо меньше тех, которых можно было ожидать ввиду неполноты и неточности некоторых наших данных.

Остается вопрос: на чей счет мы отнесем вину за ошибки, на которые указывают имеющиеся небольшие расхождения? Будет ли это вина М, M', V, V', Р или T? Как мы будем исправлять вычисленные нами цифры? Мы можем ограничиться общими принципами, что наименьшие исправления, всего вероятнее, будут самыми правильными. Наименьшие исправления включают взаимное согласование между всеми шестью факторами, а каждое отдельное согласование будет уменьшать существующее несоответствие. Таким путем каждый вычисленный фактор рассматривается как имеющий некоторое значение и оказывающий некоторое влияние на исправление всех остальных; таким образом, каждый отдельный фактор будет требовать чрезвычайно мало изменений. Произведенные в различных факторах изменения сделаны пропорционально предполагаемой относительной их подверженности ошибкам.

Результаты этих исправлений показаны ниже, на рис. 12, 13 и 14, и на предыдущем рис. 11. Каждый из этих рисунков относится к одному из факторов уравнения обмена, как непосредственно вычисленному, так и окончательно согласованному (пунктирные линии). Если же все факторы согласованы между собой таким образом, то они вполне соответствуют уравнению обмена.

На рис. 12 мы видим, что изменения, сделанные в цифрах для М и M', так ничтожны, что ими почти можно пренебречь, так как они обычно много меньше 1%. Изменения для V и V', показанные на рис. 13, несколько больше, но тоже малы, так как обычно не достигают 2%. Изменения для T, как показано на рис. 14, хотя немного больше, чем предыдущие, но тем не менее настолько малы и однообразны, что все время сохраняют почти полный параллелизм между первоначально вычисленными и измененными кривыми. Разница редко превышает 10%. Изменения для Р показаны на приведенном выше рис. 11; верхняя кривая представляет первоначальные, а пунктирная средняя кривая - измененные величины. Чрезвычайно тесный параллелизм между первоначальной и измененной кривыми здесь также очевиден. Разница редко превышает 3%.

Конечно, самый взыскательный критик не мог бы требовать большей точности результатов и соответствия их с теорией уравнения обмена, чем показывают приведенные нами статистические данные. Исправления, которые нужно было сделать для того, чтобы привести к совершенному согласованию первоначально вычисленные шесть величин, значительно меньше вероятных ошибок в этих самых цифрах. Еще не зная, насколько окончательные результаты будут гармонировать, я сделал некоторые приблизительные вычисления вероятных ошибок. Вероятная ошибка для М оказалась 2 или 3%, для M' - 2 или 3, для V - от 5 до 10, для V' - от 5 до 10 и для Т - от 5 до 10%. Иначе говоря, наши статистические данные рассматривались только как грубые и приблизительные, однако окончательное “излечение”, необходимое для согласования их между собой, как мы видели, редко превышало 2%, будучи меньше 1% для М и М', меньше 2% для V и V', меньше 3% для Р и меньше 4% для Т. Таким образом, мы можем заключить, что цифры подходят друг к другу ближе, чем этого можно было ожидать ввиду известной их неточности.

Исправления, произведенные нами в различных факторах, настолько незначительны, что было бы рискованным пытаться специфически объяснить их. Ошибки, которые в них, вероятно, встречаются, могут происходить от многочисленных причин, как, например, от изменения соотношения между переводными и обычными чековыми сделками в Нью-Йоркской расчетной палате, или от ошибок и неточности и неполноты в статистических данных о торговле зерном и т.д., или от ошибок в виде переоценок или недооценок отклонения от нормы тех особых дней в 1896 и 1909 гг., в которые были собраны статистические данные о депозитах, сделанных в банки, или же от переоценки или недооценки депозитов, о которых не было получено сведений, или еще от недооценки или переоценки золота в Соединенных Штатах, или от недооценки или переоценки заработной платы и многих других более мелких, но часто показательных элементов в наших вычислениях.

Источники только что перечисленных ошибок были названы в порядке их вероятной важности. Может быть, знаменательно, что наибольшие расхождения приходятся на 1896 - 1898 гг., когда данные для Т были наиболее дефективны, и на 1900, 1903 и 1907 гг., которые были годами кризисов или годами приближения кризисов.