Законы Кирхгофа
I закон Кирхгофа:алгебраическая сумма комплексов токов в ветвях, сходящихся в узле электрической цепи, равна нулю:
II закон Кирхгофа:алгебраическая сумма комплексов ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжений в ветвях этого контура:
Комплекс полной мощности определяется:
где S = UI – полная мощность; P = UI cosφ – активная мощность; Q = UI sinφ – реактивная мощность;
Рис. 3.1
Если ток изменяется по синусоидальному закону i = Im sin (ωt + ψi), то и напряжение изменяется по тому же закону u = Um sin(ωt + ψu). Законы изменения тока и напряжения во времени показаны на рис.3.1, б. Изображающие их векторы В символической (комплексной) форме закон Ома в общем случае запишется:
где Для действующих значений закон Ома
Мощность, потребляемая резистивным элементом, называется активной мощностью. Эта мощность расходуется на нагрев активного сопротивления резистивного элемента. Количественно она определяется как средняя мощность за период:
Конденсатор в цепи переменного тока (рис. 3.2, а). Основным параметром конденсатора является емкость С, характеризующая его способность накапливать электрическую энергию. Так как конденсатор обладает незначительным активным сопротивлением, то в первом приближении его можно считать идеальным элементом (чисто емкостным).
Рис. 3.2 Сопротивление идеального конденсатора определяется как
и называется реактивным емкостным сопротивлением. Здесь С – емкость конденсатора. Закон Ома для действующих значений тока и напряжения для цепи с идеальным конденсатором
в комплексной форме:
где Среднее значение мощности за период в цепи с идеальным конденсатором равно нулю:
В цепи с идеальным конденсатором происходит непрерывное колебание (обмен) энергии между источником и электрическим полем конденсатора без затраты энергии источника. Поэтому конденсатор получил название реактивного элемента. Параметр, характеризующий энергию, которой обмениваются источник и конденсатор, называется реактивной мощностью и обозначается QC. Количественно она определяется:
Катушка в цепи переменного тока. В электрической цепи с идеальной индуктивной катушкой (рис. 3.3, а) активное сопротивление RK= 0. При приложении переменного напряжения u=UMsinωt по катушке протекает ток i=Imsin(ωt – π/2) (рис. 3.3, б), т.е. ток отстает по фазе от напряжения на угол π/2 и вектор İ отстает от вектора
Сопротивление идеальной катушки XL = ωL = 2πfL, Ом, называют индуктивным сопротивлением катушки. Здесь L – индуктивность катушки. Закон Ома для действующих значений тока и напряжения для цепи с идеальной индуктивной катушкой:
в комплексной форме:
где Среднее за период значение мощности цепи с идеальной катушкой Рср= 0, т. е. в цепи с идеальной индуктивной катушкой происходит непрерывное колебание (обмен) энергии между источником и магнитным полем катушки без затрат энергии источника. Поэтому индуктивная катушка получила название реактивного элемента, а мощность – реактивной QL. Количественно она определяется:
При приложенном к реальной катушке напряжении u = UM sinωt по ней протекает ток i = IMsin(ωt – φi). To есть ток отстает по фазе от напряжения на угол φК = φu – φi (рис. 3.4, в), который из-за наличия в катушке активного сопротивления RK всегда меньше 90°. Вектор Сопротивление реальной индуктивной катушки:
в комплексной форме:
где Закон Ома для действующих значений тока и напряжения:
в комплексной форме:
Активная мощность в реальной индуктивной катушке:
где коэффициент мощности
Реактивная мощность
Трансформаторы и синхронные генераторы конструктивно рассчитываются для работы при определенных значениях напряжения и тока. Поэтому их номинальную мощность, от которой зависит их стоимость и размеры, часто характеризуют не активной, а полной мощностью:
Активная, реактивная и полная мощности связаны следующим соотношением:
в комплексной форме:
Здесь Последовательное соединение из резистивного элемента, реальной индуктивной катушки и конденсатора представлено на рис. 3.5, а. Схема замещения такой цепи представлена на рис. 3.5, б. Полное сопротивление такой цепи:
В комплексной форме оно записывается
Ток, протекающий по цепи:
где RK = ZK cos φк, XL = ZK sin φк. В комплексной форме:
Напряжения на зажимах цепи:
В комплексной форме:
На основании ІІ закона Кирхгофа напряжение, приложенное к цепи: – для мгновенных значении
– для действующих значении
где Uak = RkI = Uk cos φk; UL = I XL = Uk sin φk; – для комплексных значении
Активная мощность цепи
Коэффициент мощности всей цепи
Коэффициент мощности катушки
где РK = RK I²; SK = UK I. Реактивная мощность
Полная мощность
Комплексная полная мощность цепи
Построение векторной диаграммы напряжений и тока для цепи, изображенной на рис. 3.5, б, следует начинать с построения вектора тока I, так как по всем элементам протекает один и тот же ток. При построении векторов напряжений необходимо учитывать фазовые сдвиги между напряжением и током для соответствующих элементов (см. рис. 3.1, 3.3, 3.4). Тогда векторная диаграмма напряжений и тока для цепи, изображенной на рис. 3.5, а, б, для которой на основании ІІ закона Кирхгофа Если в цепи, изображенной на рис. 3.5, а, б, реактивные сопротивления равны ( Домашнее задание Изучите основные теоретические положения, относящиеся к работе резистивного, индуктивного и емкостного элементов в цепях синусоидального тока. Рассмотрите схемы опытов и построение векторных диаграмм напряжений. Выпишите формулы расчетов параметров, представленных в таблицах лабораторной работы. Запишите условия возникновения резонанса напряжений. Порядок выполнения работы 1. Соберите цепь по схеме рис. 3.6. 2. При помощи ЛАТРа установите напряжение 100 В и проведите три замера, меняя сопротивление R1. Показания приборов занесите в табл. 3.1.
Рис. 3.6
4. Соберите цепь по схеме рис. 3.7.
Рис. 3.7
6. Установите заданное значение сопротивления R1. При неизменном напряжении 100 В и сопротивлении R1, изменяя емкость конденсаторов С, сделайте три опыта. Показания приборов запишите в табл. 3.2. Таблица 3.2
7. 8. 9. 10. 11. 12. 7. По опытным данным рассчитайте параметры всей цепи и конденсатора. Постройте векторные диаграммы токов и напряжений.
Рис. 3.8
9. Установите с помощью Т3 напряжение 100 В, выключите конденсаторы, установите заданные значения R1 и ZK. Увеличивая количество включенных конденсаторов, убедитесь в том, что в схеме ток будет возрастать (до резонанса), достигнув максимума при резонансе напряжений. При дальнейшем увеличении емкости ток начинает уменьшаться (после резонанса). Проделайте один опыт до резонанса, второй – при резонансе и третий – после резонанса. Результаты измерений запишите в табл. 3.3. 10. По опытным данным рассчитайте параметры всей цепи, реостата, конденсатора и катушки индуктивности (табл. 3.3). Постройте векторные диаграммы токов и напряжений. Таблица 3.3
Контрольные вопросы
1. Основные параметры синусоидального тока. 2. Закон Ома в символической форме. 3. Законы Кирхгофа в символической форме. 4. Напишите уравнения электрического состояния для каждой схемы в символической форме. 5. Запишите комплексные полные сопротивления каждой цепи. 6. Резистивный элемент в цепи переменного тока. 7. Конденсатор в цепи переменного тока. 8. Индуктивность в цепи переменного тока. 9. Коэффициент мощности и его значение.
10. Условия возникновения резонанса напряжения. 11. Чему равен cosφ при резонансе напряжений? 12. Чему равна реактивная мощность всей цепи при резонансе? Литература
[1, §2.1.–2.12; 2, §2.1–2.15; 3, §2.1–2.9].
Лабораторная работа №4 ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ. РЕЗОНАНС ТОКОВ Цель работы Выработка умения анализировать электрическое состояние цепи переменного тока с параллельным соединением резистора, катушки индуктивности и конденсатора, ознакомление с условиями возникновения резонанса токов. Основные теоретические положния Особенностью расчета разветвленных цепей переменного тока является то, что при расчете используется метод проводимостей, с помощью которого определяют все искомые величины. При таком подходе выражение для определения полной проводимости ветвей или цепи с параллельным соединением элементов имеет такой же достаточно простой вид, как и выражение для определения полного сопротивления в цепи с последовательным соединением элементов:
Здесь Y – полная проводимость цепи или ветви; g – активная проводимость ветви; bL – индуктивная проводимость ветви; bC – емкостная проводимость ветви. В символической (комплексной) форме полная проводимость цепи или ветви записывается в виде
Закон Ома для определения величины тока цепи или ветви:
в комплексной форме
U, I – соответственно действующее значение напряжения и тока; φi, φu – соответственно начальные фазы тока и напряжения; е – основание натурального логарифма. В ряде случаев расчет разветвленных цепей переменного тока можно проводить не через проводимости, а через сопротивления. Наиболее удобно в этом случае проводить расчет, используя символический (комплексный) метод, так как он позволяет применять все те же методы расчета, как и для цепей постоянного тока. Рассмотрим несколько примеров расчета разветвленных цепей переменного тока.
Рис. 4.1 Проводимости ветвей цепи:
где R – сопротивление резистивного элемента;
Полная проводимость цепи
Комплексная полная проводимость цепи
Токи, протекающие в ветвях, и общий ток цепи
Общий ток цепи, в комплексной форме:
где
Построение векторной диаграммы токов и напряжений для цепи, изображенной на рис. 4.1, а (и подобных цепей), следует начинать с построения вектора напряжения, так как напряжение одно и то же. При построении векторов токов необходимо учитывать характер сопротивлений, по которым протекают токи. Следовательно, векторы тока и напряжения на резисторе совпадают по фазе. Ток, протекающий по идеальной индуктивности, отстает по фазе от приложенного напряжения на угол 90°. Так как конденсатор обладает незначительным активным сопротивлением, его можно считать идеальным емкостным элементом, а ток, протекающий по конденсатору, опережает приложенное к нему на1пряжение на угол 90°. Тогда векторная диаграмма токов и напряжения для цепи, в которой на основании I закона Кирхгофа В случае, когда в цепи (рис. 4.1, а) реактивные проводимости будут равны между собой (bl = bС), то и реактивные токи также будут равны между собой (IL = IC) и взаимно компенсируются, здесь имеет место явление резонанса токов. В этом случае общий ток в цепи IO и напряжение на входе цепи U совпадают по фазе (φ = φu – φio =0, cosφ =1). Общий ток в цепи равен току, проходящему через резистор:
Мощности цепи (рис. 4.1, а): активная
реактивная
полная
Комплексная полная мощность
где Б. Цепь из двух параллельных ветвей Проводимости ветвей цепи (рис. 4.2, а):
Полная проводимость ветвей цепи
Комплексная полная проводимость ветвей цепи
Токи в ветвях и общий ток цепи:
В комплексной форме токи в ветвях и общий ток цепи:
Расчет электрической цепи при параллельном соединении ветвей можно выполнить и без предварительного определения активных и реактивных проводимостей, представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями. Для цепи, изображенной на рис. 4.2, а, полное сопротивление ветвей определяется:
Токи в ветвях и общий ток цепи:
где
Комплексные полные сопротивления:
(4.21)
Токи в ветвях и общий ток в цепи:
Векторная диаграмма токов и напряжения для цепи представлена на рис. 4.2, б. Мощности цепи (рис. 4.2, а): активная
реактивная
полная
Домашнее задание Изучите основные теоретические положения, относящиеся к разветвленным цепям переменного тока, понятия о проводимостях параллельных ветвей в грамм токов. Принцип построения векторных диаграмм токов. Выпишите формулы расчета параметров, указанных в таблицах лабораторной работы. Запишите условия возникновения резонанса токов. Порядок выполнения работы
1.2. Введите полностью реостат R1. Установите заданное напряжение и в течение опыта поддерживайте постоянным это значение. 1.3. Изменяя сопротивление R1, произведите три опыта. Показания приборов запишите в табл. 4.1. 1.4. По результатам опытов вычислите требуемые параметры электрической цепи (табл. 4.1). Постройте векторные диаграммы токов и напряжения. 1.5. Изменяя индуктивность катушки перемещением ее сердечника, произведите три опыта. Показания приборов занесите в табл. 4.1. 1.6. По результатам опытов вычислите требуемые параметры электрической цепи (табл. 4.1). Постройте векторные диаграммы токов и напряжения. 2. Параллельное соединение резистора и конденсатора. 2.1. Соберите цепь по схеме рис. 4.4.
Рис.4.4 Таблица 4.1
Таблица 4.2
2.3. По результатам опытов вычислите требуемые параметры электрической цепи (табл. 4.2). Постройте векторные диаграммы токов и напряжения. 2.4. Установите ток I1 согласно значению, указанному в табл. 4.2. Изменяя емкость конденсаторов, проведите 3 опыта, результаты которых занесите в табл. 4.2. 2.5. По результатам опытов вычислите требуемые параметры электрической цепи (табл. 4.1). Постройте векторные диаграммы токов и напряжения. 3. Параллельное соединение резистора, катушки индуктивности и конденсатора.
Рис. 4.5
3.2. Введите полностью реостат R1. Установите напряжение 100 В. 3.3. Установите емкость конденсаторов С = 0 (конденсаторы выключены). Проведите первый замер. 3.4. Постепенно включая конденсаторы, добейтесь минимального значения общего тока (резонанс токов). Проведите второй замер. 3.5. Установите максимальную емкость конденсаторов. Проведите третий замер. Результаты опытов занесите в табл. 4.3.
Таблица 4.3
Контрольные вопросы 1. Напишите уравнения электрического состояния для каждой схемы в комплексной форме. 2. Запишите комплексные значения полной проводимости каждой 3. Переход от векторной диаграммы токов к треугольнику проводимостей и мощностей. 4. Влияние параметров параллельной цепи на cosφ. 5. Условия возникновения резонанса токов. 6. Электрические явления, возникающие при резонансе токов. Литература: [1, §2.13, 2.17, 2.19; 2, §2.15–2.17, 2.20,2.21; 3, §2.13–2.19].
Лабораторная работа №5 ИССЛЕДОВАНИЕ ТРЕХФАЗНЫХ ПРИЕМНИКОВ, СОЕДИНЕННЫХ ПО СХЕМАМ ЗВЕЗДА И ТРЕУГОЛЬНИК Цель работы Опытная проверка основных закономерностей трехфазной электрической цепи при симметричной и несимметричной нагрузках, а также влияния нейтрального провода на соотношение фазных и линейных трехфазных напряжений и токов приемника. Трехфазная электрическая цепь при соединении приемников звездой.
При соединении фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью), а начало фаз выходит к зажимам, обозначаемым соответственно А, В и С (рис. 5.1). Провод, соединяющий нейтральные точки генератора N и приемника n, называется нейтральным, остальные провода – линейными. Напряжения между началом и концом каждой фазы источника или приемника называют фазными. Фазными токами называются токи в обмотках генератора или в сопротивлениях фаз нагрузки. Напряжения между началами фаз называются линейными. Линейными называются и токи в линейных проводах. При соединении звездой линейные токи равны фазным (IЛ = IФ). Линейные напряжения при соединении звездой являются векторной разностью соответствующих фазных напряжений: Соответствующие векторные диаграммы фазных и линейных напряжений представлены на рис. 5.2, а, б.
Рис. 5.2 Векторы линейных напряжений
Нагрузка считается симметричной, если равны комплексные полные сопротивления фаз
Рис. 5.3 Из диаграммы следует, что При несимметричной нагрузке ( Токи в фазах приемника составляют несимметричную систему. Появляется ток в нейтральном проводе Величину тока каждой фазы и сдвиг фаз определяют по следующим формулам:
Если при несимметричной нагрузке не будет нейтрального провода (при ZN ≠ 0), то фазные напряжения приемника не будут равны соответствующим напряжениям источника. Нейтральная точка n сместится из центра треугольника линейных напряжений N. Между нейтральными точками источника и приемника возникает напряжение UnN, называемое напряжением относительно нейтрали или напряжением между нейтралями (рис. 5.4, б), которое может быть определено из соотношения:
где
Пренебрегая сопротивлениями линейных проводов, получим соотношения между фазными напряжениями генератора и нагрузки:
Линейные и фазные токи можно определить из следующих соотношений:
Ток в нейтральном проводе:
Векторная диаграмма для данного случая представлена на рис. 5.4, б.
|

 (3.2)
(3.2) (3.3)
(3.3)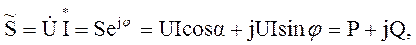 (3.4)
(3.4) – сопряженный комплекс тока.
– сопряженный комплекс тока. Резистивный элемент в цепи переменного тока (рис. 3.1, а) обладает активным сопротивлением.
Резистивный элемент в цепи переменного тока (рис. 3.1, а) обладает активным сопротивлением.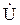 и
и  (рис. 3.1, в) также совпадают по фазе, т. е. φ
(рис. 3.1, в) также совпадают по фазе, т. е. φ 
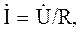 (3.5)
(3.5)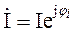 ,
,  .
. (3.6)
(3.6)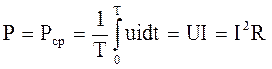 (3.7)
(3.7)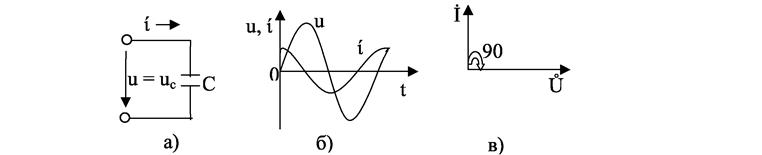 При приложенном к конденсатору напряжении u = UM sinωt через него протекает ток i = IMsin(ωt +π/2), т. е. ток опережает по фазе напряжение на четверть периода (рис. 3.2, б, в).
При приложенном к конденсатору напряжении u = UM sinωt через него протекает ток i = IMsin(ωt +π/2), т. е. ток опережает по фазе напряжение на четверть периода (рис. 3.2, б, в).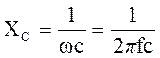 (3.8)
(3.8)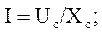 (3.9)
(3.9)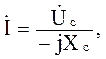 (3.10)
(3.10) ;
; 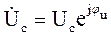 .
. (3.11)
(3.11) (3.12)
(3.12) на угол π/2 (рис. 3.3, в).
на угол π/2 (рис. 3.3, в). Рис. 3.3
Рис. 3.3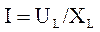 (3.13)
(3.13)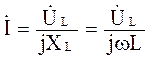 (3.14)
(3.14)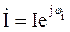 ;
; 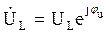 .
.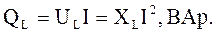 (3.15)
(3.15)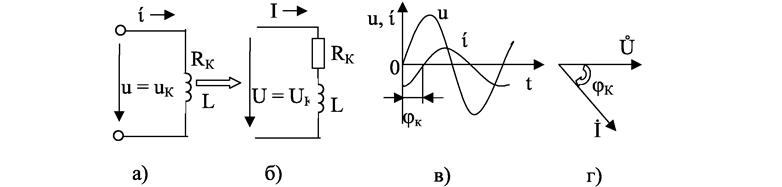 Электрическая цепь с реальной индуктивной катушкой (рис. 3.4, а). Все реальные цепи, содержащие индуктивность, обладают активным сопротивлением RK (сопротивление провода катушки, подводящих проводов и т. д.). Такую реальную индуктивную катушку можно представить из последовательно соединенных идеальных элементов: идеальной индуктивной катушки L и резистивного элемента с активным сопротивлением RK (рис. 3.4, б).
Электрическая цепь с реальной индуктивной катушкой (рис. 3.4, а). Все реальные цепи, содержащие индуктивность, обладают активным сопротивлением RK (сопротивление провода катушки, подводящих проводов и т. д.). Такую реальную индуктивную катушку можно представить из последовательно соединенных идеальных элементов: идеальной индуктивной катушки L и резистивного элемента с активным сопротивлением RK (рис. 3.4, б).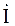 отстает от вектора
отстает от вектора 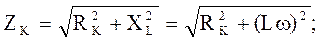 (3.16)
(3.16) , (3.17)
, (3.17) – модуль комплексного полного сопротивления реальной индуктивной катушки;
– модуль комплексного полного сопротивления реальной индуктивной катушки;  – его аргумент.
– его аргумент.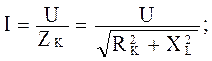 (3.18)
(3.18) (3.19)
(3.19) (3.20)
(3.20) (3.21)
(3.21) (3.22)
(3.22) (3.23)
(3.23)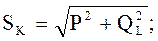 (3.24)
(3.24)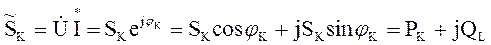 (3.25)
(3.25)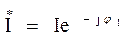 – сопряженный комплекс тока.
– сопряженный комплекс тока. (3.26)
(3.26) (3.27)
(3.27) (3.28)
(3.28)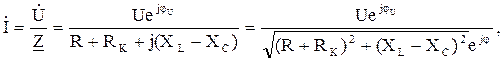 (3.29)
(3.29) где φ = φu – φi
где φ = φu – φi

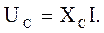 (3.30)
(3.30)
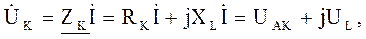
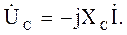 (3.31)
(3.31)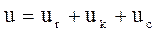 (3.32)
(3.32) (3.33)
(3.33)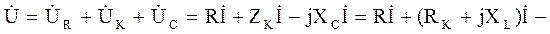
 (3.34)
(3.34)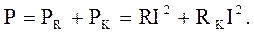 (3.35)
(3.35)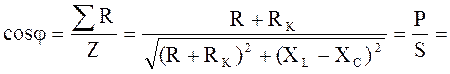
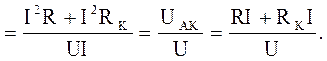 (3.36)
(3.36) (3.37)
(3.37) (3.38)
(3.38)
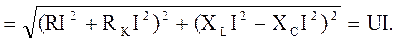 (3.39)
(3.39) (3.40)
(3.40)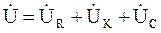 , при условии, что
, при условии, что  , следовательно,
, следовательно, 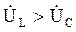 , будет иметь вид, представленный на рис. 3.5, в.
, будет иметь вид, представленный на рис. 3.5, в. ), следовательно, напряжения
), следовательно, напряжения 
 на реактивных элементах также будут равны (
на реактивных элементах также будут равны ( ), то в такой цепи возникает резонанс напряжений, при котором напряжения на реактивных элементах могут значительно превысить напряжения на входе цепи и вывести их из строя (пробой в конденсаторе, межвитковые замыкания в катушке), а значит, нарушить нормальную работу в цепи. Поэтому явление резонанса напряжений недопустимо в силовых электрических цепях.
), то в такой цепи возникает резонанс напряжений, при котором напряжения на реактивных элементах могут значительно превысить напряжения на входе цепи и вывести их из строя (пробой в конденсаторе, межвитковые замыкания в катушке), а значит, нарушить нормальную работу в цепи. Поэтому явление резонанса напряжений недопустимо в силовых электрических цепях.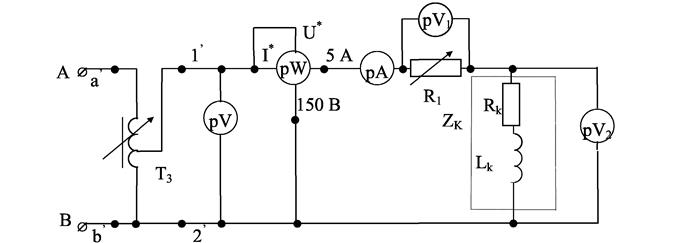 3. По опытным данным рассчитайте параметры всей цепи и катушки индуктивности. Постройте векторные диаграммы токов и напряжений.
3. По опытным данным рассчитайте параметры всей цепи и катушки индуктивности. Постройте векторные диаграммы токов и напряжений. Таблица 3.1
Таблица 3.1 5. Полностью введите реостат R1. Включите половину конденсаторов. Установите с помощью Т3 напряжение 100 В. Изменяя сопротивление R1, сделайте три замера, при этом поддерживайте напряжение 100 В. Показания приборов запишите в табл. 3.2.
5. Полностью введите реостат R1. Включите половину конденсаторов. Установите с помощью Т3 напряжение 100 В. Изменяя сопротивление R1, сделайте три замера, при этом поддерживайте напряжение 100 В. Показания приборов запишите в табл. 3.2.
 8. Соберите цепь по схеме рис. 3.8.
8. Соберите цепь по схеме рис. 3.8.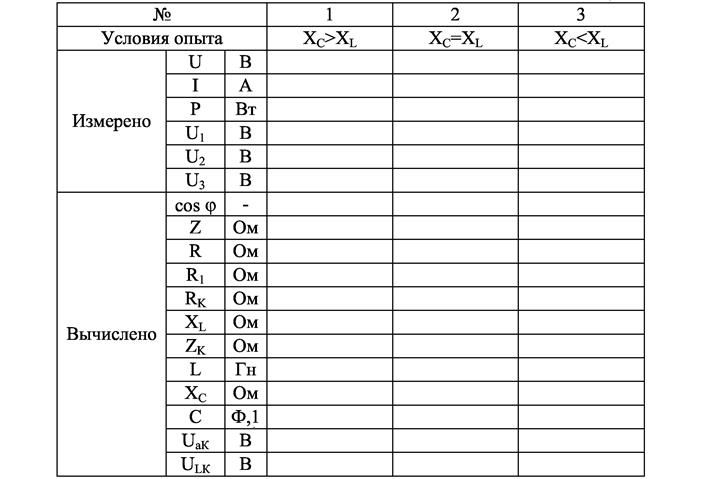
 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) – комплекс действующего значения тока;
– комплекс действующего значения тока; – комплекс действующего значения напряжения;
– комплекс действующего значения напряжения; А. Цепь с параллельным соединением идеализированных элементов (рис. 4.1).
А. Цепь с параллельным соединением идеализированных элементов (рис. 4.1).

 (4.5)
(4.5)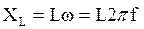 – сопротивление идеальной индуктивной катушки;
– сопротивление идеальной индуктивной катушки;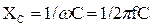 – сопротивление идеального конденсатора.
– сопротивление идеального конденсатора. (4.6)
(4.6)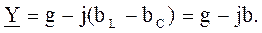 (4.7)
(4.7)

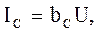 (4.8)
(4.8)
 (4.9)
(4.9)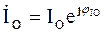 – комплекс общего тока;
– комплекс общего тока; – комплекс напряжения, приложенного к цепи;
– комплекс напряжения, приложенного к цепи;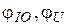 – соответственно начальные фазы тока и напряжения.
– соответственно начальные фазы тока и напряжения. , при условии, что bl > bС, следовательно, IL > IС, будет иметь вид, представленный на рис. 4.1, б.
, при условии, что bl > bС, следовательно, IL > IС, будет иметь вид, представленный на рис. 4.1, б. (4.10)
(4.10)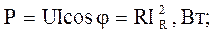 (4.11)
(4.11)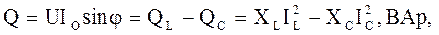 (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14) – сопряженный комплекс общего тока
– сопряженный комплекс общего тока – активная проводимость первой ветви;
– активная проводимость первой ветви;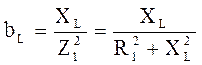 – индуктивная проводимость первой ветви;
– индуктивная проводимость первой ветви; – активная проводимость второй ветви;
– активная проводимость второй ветви;
 – емкостная проводимость второй ветви.
– емкостная проводимость второй ветви.

 (4.15)
(4.15)

 (4.16)
(4.16)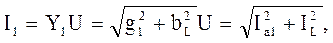
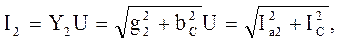 (4.17)
(4.17)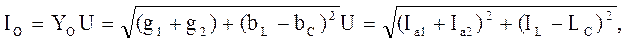 где
где  – активная составляющая тока I1;
– активная составляющая тока I1;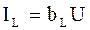 – индуктивная составляющая тока I1;
– индуктивная составляющая тока I1; – активная составляющая тока I2;
– активная составляющая тока I2; – ёмкостная составляющая тока I1;
– ёмкостная составляющая тока I1;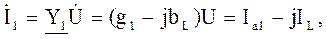
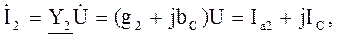 (4.18)
(4.18)

 (4.19)
(4.19)
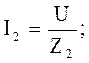
 (4.20)
(4.20) ;
;  ;
;  ;
;  .
.
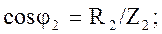




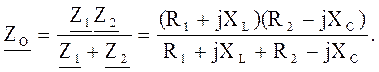

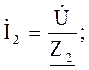
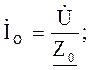
 (4.22)
(4.22)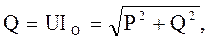 (4.23)
(4.23)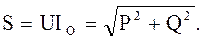 (4.24)
(4.24) 1. Параллельное соединение резистора и катушки индуктивности 1.1. Соберите цепь по схеме рис. 4.3.
1. Параллельное соединение резистора и катушки индуктивности 1.1. Соберите цепь по схеме рис. 4.3. 2.2. Введите полностью реостат R1. Установите заданное напряжение и в течение опыта поддерживайте это напряжение постоянным. Изменяя сопротивление R1, проведите три опыта, результаты которых занесите в табл. 4.2.
2.2. Введите полностью реостат R1. Установите заданное напряжение и в течение опыта поддерживайте это напряжение постоянным. Изменяя сопротивление R1, проведите три опыта, результаты которых занесите в табл. 4.2.
 3.1. Соберите цепь по схеме (рис. 4.5).
3.1. Соберите цепь по схеме (рис. 4.5).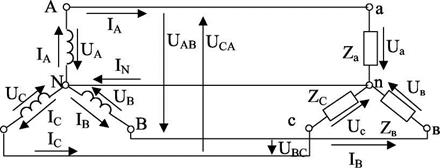
 ,
, 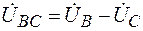 ,
,  (5.1)
(5.1)
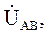
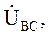
 опережают по фазе, соответственно, векторы фазных напряжений
опережают по фазе, соответственно, векторы фазных напряжений 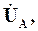
 и
и  на угол 30 (рис. 5.2, а). Векторы фазных и линейных напряжений в случае симметричной системы образуют три равнобедренных треугольника с углом 30°. Из этих треугольников можно вывести, что величина каждого из векторов линейных напряжений в
на угол 30 (рис. 5.2, а). Векторы фазных и линейных напряжений в случае симметричной системы образуют три равнобедренных треугольника с углом 30°. Из этих треугольников можно вывести, что величина каждого из векторов линейных напряжений в 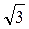 раз больше величины вектора фазного напряжения.
раз больше величины вектора фазного напряжения.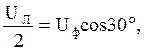 т. е.
т. е.  . (5.2)
. (5.2)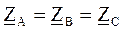
 Векторная диаграмма, соответствующая случаю симметричной на грузки, представлена на рис. 5.3.
Векторная диаграмма, соответствующая случаю симметричной на грузки, представлена на рис. 5.3.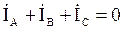 , т. е. при симметричной нагрузке ток в нейтральном проводе отсутствует (IN = 0).
, т. е. при симметричной нагрузке ток в нейтральном проводе отсутствует (IN = 0).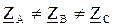 ), благодаря нейтральному проводу, фазные напряжения приемника также образуют симметричную систему.
), благодаря нейтральному проводу, фазные напряжения приемника также образуют симметричную систему. .
.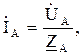
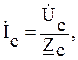


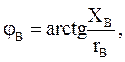
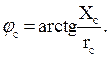 (5.3)
(5.3) Для определения тока в нейтральном проводе строят векторную диаграмму (рис. 5.4, а) и графически определяют вектор тока İN путем геометрического сложения векторов фазных токов
Для определения тока в нейтральном проводе строят векторную диаграмму (рис. 5.4, а) и графически определяют вектор тока İN путем геометрического сложения векторов фазных токов 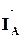 ,
, 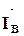 и
и 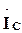 .
.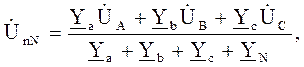 (5.4)
(5.4)
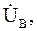
 – фазные напряжения генератора;
– фазные напряжения генератора;


 – комплексы проводимостей фаз нагрузки и нейтрального провода
– комплексы проводимостей фаз нагрузки и нейтрального провода
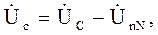
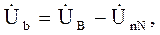
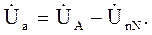 (5.5)
(5.5)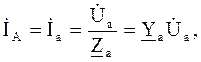
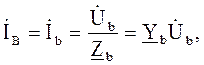
 (5.6)
(5.6) (5.7)
(5.7)


