Потенциальная диаграмма
Под потенциальной диаграммой понимается график распределения потенциалов вдоль электрической цепи. По оси абсцисс откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, на оси ординат – потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме. Домашнее задание Изучить закон Ома и законы Кирхгофа, а также распределение напряжений и токов в электрических цепях с последовательным, параллельным и смешанным соединением приемников в зависимости от величины их сопротивлений. Запишите формулы, определяющие общее сопротивление для данных схем. Порядок выполнения работы 1. Последовательное соединение приемников. 1.1. Соберите цепь по схеме рис. 2.3. 1.2. Введите полностью реостаты R1 и R2. Установите с помощью автотрансформатора Т1 заданное напряжение. При неизменном сопротивлении R1 уменьшите сопротивление R2 так, чтобы ток изменился в заданных пределах. Запишите показания приборов в табл.2.1. Для каждого опыта вычислите значения мощностей Р1, Р2, Робщ и сопротивлений R1, R2, Rэ. 1.3. Постройте на одном рисунке графики
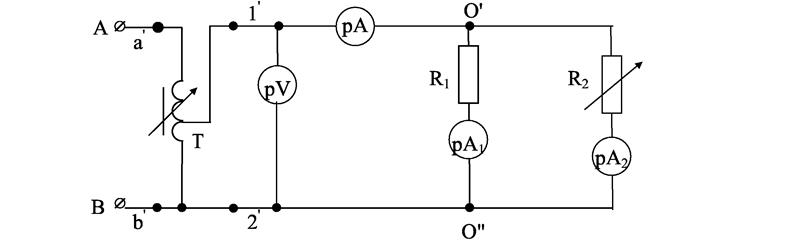
Рис. 2.3 Таблица 2.1
2. Параллельное соединение приемников. 2.1. Соберите цепь по схеме рис. 2.4. 2.2. Введите реостаты R1 и R2. Изменяя сопротивление R2 так, чтобы ток изменился в заданных пределах, запишите показания приборов в табл. 2.2. Для каждого опыта вычислите значения мощностей Р1, Р2, Робщ и проводимостей g1, g2, gэ. 2.3. Постройте на одном рисунке графики
2.4. Проведите анализ и сделайте выводы о работе схемы рис. 2.4. Рис. 2.4 Таблица 2.2
3. Смешанное соединение приемников. 3.1. Соберите цепь по схеме рис. 2.5. 3.2. Введите реостаты. Изменяя сопротивление R3 так, чтобы ток изменялся в заданных пределах, запишите показания приборов в табл. 2.3. Для каждого опыта вычислите значения мощностей Р1, Р2, Р3, Робщ, сопротивлений R1, R2, R3, Rэ. 3.3. Постройте графики
Рис. 2.5
Контрольные вопросы 1. Основные законы линейных электрических цепей. 2. Основные свойства цепей с последовательным, параллельным и смешанным соединением приемников. 3. Баланс мощности для каждой из изученных схем. 4. Расчет электрических цепей методом эквивалентных преобразований. 5. Почему при изменении R3 в смешанной цепи происходят также изменения токов, напряжений и мощностей на R1 и R2? Литература: [1, §1.1 – 1.9; 2, §1.1–1.4; §1.6 – 1.10]. Лабораторная работа №3 ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ. РЕЗОНАНС НАПРЯЖЕНИЙ Цель работы Выработка умения анализировать электрическое состояние цепи переменного тока с последовательным соединением резистора, катушки индуктивности и конденсатора, ознакомление с условиями возникновения резонанса напряжений и последствиями этого режима. Основные теоретические положения Переменным током называется электрический ток, периодически изменяющийся по величине и направлению. В электротехнике наибольшее распространение получили синусоидальные токи (изменяющиеся по закону синусоиды). Основными параметрами синусоидального тока являются: i – мгновенное значение тока; Im – амплитуда тока; I = Im/ Icp = 2/πIm – среднее значение тока; Т – период тока; f – частота; ω = 2πf – угловая частота; φ – начальная фаза. Аналогичными параметрами характеризуются синусоидальные напряжения и ЭДС. Электрические цепи с переменными токами по сравнению с цепями постоянного тока имеют ряд особенностей, которые усложняют анализ процессов в цепях. Применение векторных диаграмм при расчете и исследовании цепей позволяют наглядно представить рассматриваемые процессы и упростить производимые расчеты. Применение символического (комплексного) метода, основанного на использовании комплексных чисел для изображения векторов переменного тока, позволяет выразить в алгебраической форме геометрические операции с векторами переменных токов и напряжений, благодаря чему все методы расчета цепей постоянного тока применимы и для цепей переменного тока. Закон Ома в символической форме:
где
U, I – соответственно действующие значения напряжения и тока; φi, φu – начальные фазы напряжения и тока;
Z – модуль комплекса полного сопротивления; φ = φu – φi – угол сдвига фаз между током и напряжением; e – основание натурального логарифма; j =
|

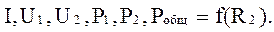
 Проведите анализ и сделайте выводы о работе схемы рис. 2.3.
Проведите анализ и сделайте выводы о работе схемы рис. 2.3.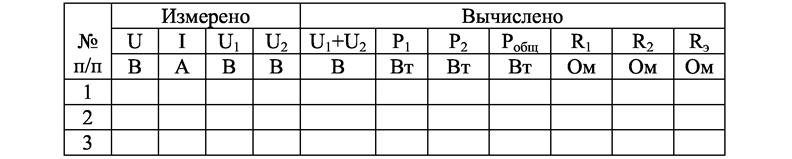
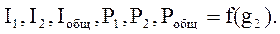


 3.4. Проведите анализ и сделайте выводы о работе схемы рис. 2.5.
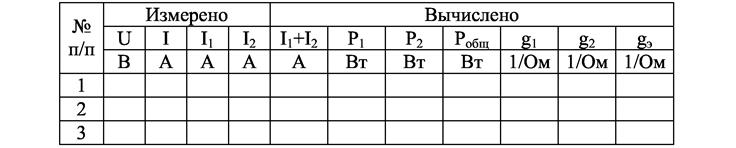
3.4. Проведите анализ и сделайте выводы о работе схемы рис. 2.5. Таблица 2.3
Таблица 2.3 – действующее значение тока;
– действующее значение тока;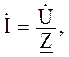 (3.1)
(3.1)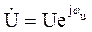 – комплекс действующего значения напряжения;
– комплекс действующего значения напряжения;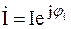 – комплекс действующего значения тока;
– комплекс действующего значения тока; – комплекс полного сопротивления;
– комплекс полного сопротивления; – мнимая единица.
– мнимая единица.


