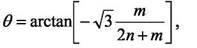Угол хиральности и диаметр нанотрубок
Структура углеродных нанотрубок Угол хиральности и диаметр нанотрубок Углеродные нанотрубки представляют собой протяженные структуры, состоящие из свернутых в однослойную (ОСНТ) или многослойную (МСНТ) трубку графитовых слоев. Известный наименьший диаметр нанотрубки - 0.714 нм, что является диаметром молекулы фуллерена С60. Расстояние между слоями практически всегда составляет 0,34 нм, что соответствует расстоянию между слоями в графите. Длина таких образований достигает десятков микрон и на несколько порядков превышает их диаметр (рис. 3). Нанотрубки могут быть открытыми или заканчиваться полусферами, напоминающими половину молекулы фуллерена. Свойства нанотрубки определяются углом ориентации графитовой плоскости относительно оси трубки. На рис.3 приведены две возможные высокосимметричные структуры нанотруб – зигзальные (zigzag) и кресельные (armchair). Но на практике большинство нанотруб не обладает такими высокосимметричными формами, т.е. в них гексагоны закручиваются по спирали вокруг оси трубы. Эти структуры называют хиральными.
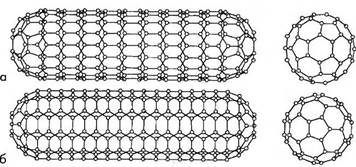
Рис.3. Идеализированные модели однослойных нанотрубок с зигзагной (а) и кресельной (б) ориентациями.
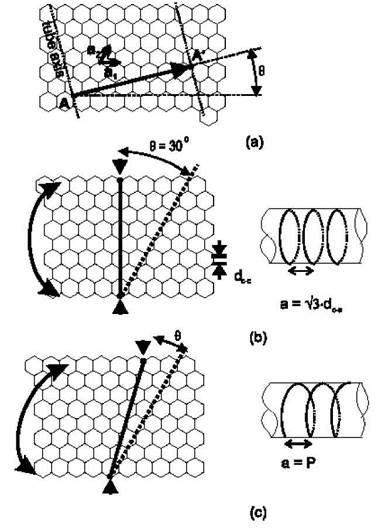
Рис. 4. Углеродные нанотрубки образуются при скручивании графитовых плоскостей в цилиндр, соединяя точку А с А'. Угол хиральности определяется как q - (а). Трубка типа «кресло», сh= (4,4) - (б). Шаг Р зависит от угла q - (с).
Существует ограниченное число схем, с помощью которых из графитового слоя можно выстроить нанотрубку. Рассмотрим точки А и А' на рис. 4а. Вектор, соединяющий А и А' определяется, как ch =na1+ma2, где n, m - действительные числа, a1, а2 - единичные вектора в графитовой плоскости. Трубка образуется при сворачивании графитового слоя и соединении точек А и А'. Тогда она определяется единственным образом вектором ch. На рис. 5 дана схема индексирования вектора решетки ch. Индексы хиральности однослойной трубки однозначным образом определяют ее диаметр:
где
Рис.5. Схема индексирования вектора решетки ch.
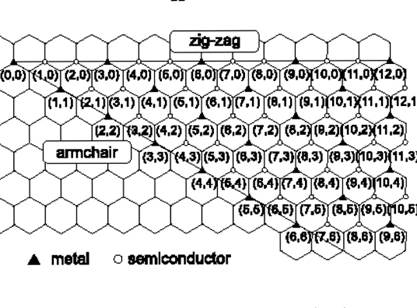
Нанотрубки типа зигзаг определяются углом Q =0°,что соответствует вектору (n, m)= (n, 0). В них связи С-С идут параллельно оси трубки (рис.3, а). Структура типа «кресло» характеризуется углом Q = ±30°, соответствующим вектору (n, m) = (2n, -n) или (n, n). Эта группа трубок будет иметь С-С связи, перпендикулярные оси трубки (рис. 3б и 4б). Остальные комбинации формируют трубки хирального типа, с углами 0°<< Q <30о. Как видно из рис. 4с, шаг спирали Р зависит от угла Q.
|

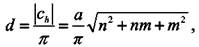
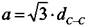 - постоянная решетки. Связь между индексами и углом хиральности дается соотношением:
- постоянная решетки. Связь между индексами и углом хиральности дается соотношением: