Определение 30. Нечетким отношением  на множествах
на множествах  называется нечеткоеподмножество декартова произведения
называется нечеткоеподмножество декартова произведения 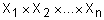 . Степень принадлежности
. Степень принадлежности  показывает степеньвыполнения отношения
показывает степеньвыполнения отношения  между элементами
между элементами  ,
,  ,
, 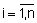 .
.
В дальнейшем будем рассматривать только бинарныенечеткие отношения, которые задаются на декартовом произведении двух множеств.Обозначим эти множества через  и
и  . Тогда задание бинарного нечеткогоотношения
. Тогда задание бинарного нечеткогоотношения  на
на 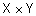 состоит вуказании всех троек
состоит вуказании всех троек 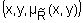 , где
, где 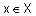 ,
,  , или, что тоже самое,
, или, что тоже самое, 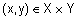 .
.
Пример 5. Задать нечеткое отношение 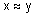 ("
("  приблизительно равно
приблизительно равно 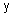 ").
").
Пусть 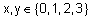 . Тогда нечеткое отношение удобнозадавать матрицей вида:
. Тогда нечеткое отношение удобнозадавать матрицей вида:
 .
.
Длянепрерывных множеств 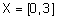 и
и 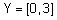 нечеткое отношение можно задатьследующей функцией принадлежности:
нечеткое отношение можно задатьследующей функцией принадлежности:  . Нечеткие отношения
. Нечеткие отношения 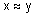 на дискретных инепрерывных множествах изображены на рис. 10.
на дискретных инепрерывных множествах изображены на рис. 10.
Пример 6. Задать нечеткое отношение "  намного меньше, чем
намного меньше, чем 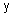 ".
".
Пусть 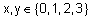 . Тогда нечеткое отношение можно задатьматрицей вида:
. Тогда нечеткое отношение можно задатьматрицей вида:
 .
.
Длянепрерывных множеств 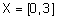 и
и 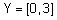 нечеткое отношение "
нечеткое отношение "  намного меньше, чем
намного меньше, чем 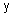 " можноопределить такой функцией принадлежности:
" можноопределить такой функцией принадлежности:  . Нечеткие отношения "
. Нечеткие отношения "  намного меньше, чем
намного меньше, чем 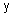 " надискретных и непрерывных множествах изображены на рис. 11.
" надискретных и непрерывных множествах изображены на рис. 11.
Как видно из примеров, нечеткие отношения являютсяболее гибкими по сравнению с традиционными отношениями. Они позволяют задать нетолько сам факт выполнения отношения, но и указывать степень его выполнения,что является очень важным для многих практических задач.
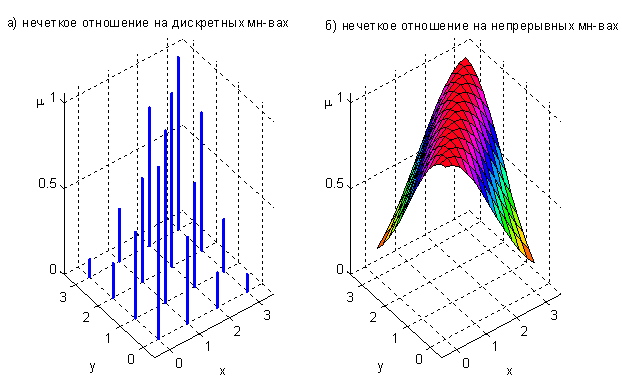
Рисунок10 - Нечеткое отношение "  приблизительно равно
приблизительно равно 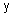 "
"
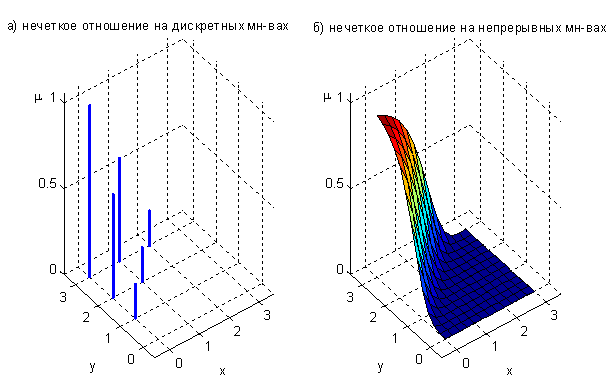
Рисунок11 - Нечеткое отношение "  намного меньше, чем
намного меньше, чем 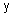 "
"
Пример 7. Задать отношение "схожий менталитет" для следующих национальностей {Украинцы(У), Чехи (Ч), Австрийцы (А), Немцы (Н)}.
Использование обычного, не нечеткого отношенияпозволяет выделить только одну пару наций со схожими менталитетами -немцев и австрийцев. Этим отношением не отражаться тот факт, что по менталитетучехи более близки к немцам, чем украинцы. Нечеткое отношение позволяет легкопредставить такую информацию:  .
.
Определение 31. Носителем нечеткого отношения  на множествах
на множествах  и
и  называетсяподмножество декартова произведения
называетсяподмножество декартова произведения 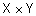 вида:
вида: 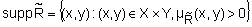 .
.
Носитель нечеткого отношения можно рассматривать какобычное отношение, связывающего все пары 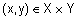 , для которых степень выполнениянечеткого отношения
, для которых степень выполнениянечеткого отношения  не равна нулю. Более полезным являетсяиспользование
не равна нулю. Более полезным являетсяиспользование 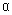 -сеченийнечеткого отношения, определения которых аналогично определениям множеств
-сеченийнечеткого отношения, определения которых аналогично определениям множеств 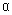 -уровня (см. раздел1.2).
-уровня (см. раздел1.2).
Определение 32. 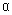 -сечением нечеткого отношения
-сечением нечеткого отношения  на
на 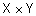 называется обычноеотношение, связывающее все пары
называется обычноеотношение, связывающее все пары 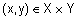 , для которых степень выполнениянечеткого отношения
, для которых степень выполнениянечеткого отношения  не меньше
не меньше 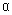 :
: 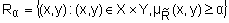 .
.
Определение 33. Нечеткое отношение  на
на 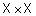 называется рефлексивным, еслидля любого
называется рефлексивным, еслидля любого 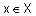 выполняетсяравенство
выполняетсяравенство  .В случае конечного множества
.В случае конечного множества  все элементы главной диагонали матрицы
все элементы главной диагонали матрицы  равны 1. Примеромрефлексивного нечеткого отношения может быть отношение "приблизительно равны".
равны 1. Примеромрефлексивного нечеткого отношения может быть отношение "приблизительно равны".
Определение 34. Нечеткое отношение  на
на 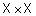 называется антирефлексивным, еслидля любого
называется антирефлексивным, еслидля любого 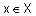 выполняетсяравенство
выполняетсяравенство 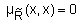 .В случае конечного множества
.В случае конечного множества  все элементы главной диагонали матрицы
все элементы главной диагонали матрицы  равны 0.Примером антирефлексивного нечеткого отношения может быть отношение"значительно больше".
равны 0.Примером антирефлексивного нечеткого отношения может быть отношение"значительно больше".
Определение 35. Нечеткое отношение  на
на 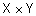 называется симметричным, еслидля любой пары
называется симметричным, еслидля любой пары 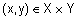 выполняетсяравенство
выполняетсяравенство 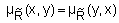 .Матрица симметричного нечеткого отношения, заданного на конечном множестве,симметричная.
.Матрица симметричного нечеткого отношения, заданного на конечном множестве,симметричная.
Определение 36. Нечеткое отношение  на
на 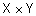 называется асимметричным, есливыражение
называется асимметричным, есливыражение 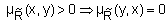 справедливодля любой пары
справедливодля любой пары 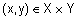 .Примером асимметричного нечеткого отношения может служить отношение "намногобольше".
.Примером асимметричного нечеткого отношения может служить отношение "намногобольше".
Определение 37. Нечеткое отношения  и
и  на
на 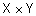 называется обратными, если длялюбой пары
называется обратными, если длялюбой пары 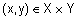 выполняетсяравенство
выполняетсяравенство 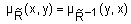 .Примером обратных нечетких отношений может служить пара "намного больше" ‑"намного меньше".
.Примером обратных нечетких отношений может служить пара "намного больше" ‑"намного меньше".

 на множествах
на множествах  называется нечеткоеподмножество декартова произведения
называется нечеткоеподмножество декартова произведения 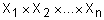 . Степень принадлежности
. Степень принадлежности  показывает степеньвыполнения отношения
показывает степеньвыполнения отношения  ,
,  ,
, 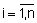 .
. и
и  . Тогда задание бинарного нечеткогоотношения
. Тогда задание бинарного нечеткогоотношения 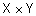 состоит вуказании всех троек
состоит вуказании всех троек 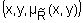 , где
, где 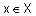 ,
,  , или, что тоже самое,
, или, что тоже самое, 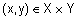 .
.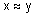 ("
("  приблизительно равно
приблизительно равно 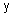 ").
").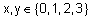 . Тогда нечеткое отношение удобнозадавать матрицей вида:
. Тогда нечеткое отношение удобнозадавать матрицей вида: .
.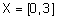 и
и 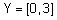 нечеткое отношение можно задатьследующей функцией принадлежности:
нечеткое отношение можно задатьследующей функцией принадлежности:  . Нечеткие отношения
. Нечеткие отношения  .
. . Нечеткие отношения "
. Нечеткие отношения " 

 .
.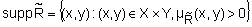 .
.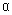 -сеченийнечеткого отношения, определения которых аналогично определениям множеств
-сеченийнечеткого отношения, определения которых аналогично определениям множеств 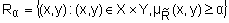 .
.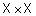 называется рефлексивным, еслидля любого
называется рефлексивным, еслидля любого  .В случае конечного множества
.В случае конечного множества 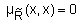 .В случае конечного множества
.В случае конечного множества 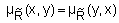 .Матрица симметричного нечеткого отношения, заданного на конечном множестве,симметричная.
.Матрица симметричного нечеткого отношения, заданного на конечном множестве,симметричная.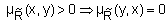 справедливодля любой пары
справедливодля любой пары  на
на 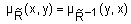 .Примером обратных нечетких отношений может служить пара "намного больше" ‑"намного меньше".
.Примером обратных нечетких отношений может служить пара "намного больше" ‑"намного меньше".


