Нечеткие логические операции
Вначале кратко напомнить основные положения обычной (булевой) логики. Рассмотрим два утверждения A и B, каждое из которых может быть истинным или ложным, т.е. принимать значения "1" или "0". Для этих двух утверждений всего существует Таблица 5 - Таблицы истинности булевой логики
Предположим, что логическое утверждение может принимать не два значения истинности, а три, например: "истинно", "ложно" и "неопределенно". В этом случае мы будем иметь дело не с двухзначной, а трехзначной логикой. Общее количество бинарных операций, а, следовательно, и таблиц истинности, в трехзначной логике равно Определение 45. Обозначим нечеткие логические переменные через
В многозначной логике логические операции могут быть заданы таблицами истинности. В нечеткой логике количество возможных значений истинности может быть бесконечным, следовательно в общем виде табличное представление логических операций невозможно. Однако, в табличной форме можно представить нечеткие логические операции для ограниченного количества истинностных значений, например, для терм-множества {"истинно", "очень истинно", "не истинно", "более-менее ложно", "ложно"}. Для трехзначной логики с нечеткими значениями истинности T -; "истинно", F -; "ложно" и T+F - "неизвестно" Л Заде предложил такие лингвистические таблицы истинности:
Применяя правила выполнения нечетких логических операций из определения 45 можно расширить таблицы истинности для большего количества термов. Как это сделать рассмотрим на следующем примере. Пример 10. Заданы следующие нечеткие истинностные значения:
Применяя правило из определения 45, найдем нечеткую истинность выражения "почти истинно ИЛИ истинно":
Сравним полученное нечеткое множество с нечетким множеством "более-менее истинно". Они почти равны, значит:
В результате выполнения логических операций часто получается нечеткое множество, которое не эквивалентно ни одному из ранее введенных нечетких значений истинности. В этом случае необходимо среди нечетких значений истинности найти такое, которое соответствует результату выполнения нечеткой логической операции в максимальной степени. Другими словами, необходимо провести так называемую лингвистическую аппроксимацию, которая может рассматриваться как аналог аппроксимации эмпирического статистическими распределения стандартными функциями распределения случайных величин. В качестве примера приведем предложенные Балдвином лингвистические таблицы истинности для показанных на рис. 15 нечетких значений истинности:
|

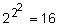 различных логических операций, из которых содержательно интерпретируются лишь пять: И (
различных логических операций, из которых содержательно интерпретируются лишь пять: И ( ), ИЛИ (
), ИЛИ ( ), исключающее ИЛИ (
), исключающее ИЛИ (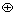 ), импликация (
), импликация ( ) и эквивалентность (
) и эквивалентность ( ). Таблицы истинности для этих операций приведены в табл. 5.
). Таблицы истинности для этих операций приведены в табл. 5.




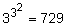 . Нечеткая логика является разновидностью многозначной логики, в которой значения истинности задаются лингвистическими переменными или термами лингвистической переменной "истинность". Правила выполнения нечетких логических операций получают из булевых логических операций с помощью принципа обобщения.
. Нечеткая логика является разновидностью многозначной логики, в которой значения истинности задаются лингвистическими переменными или термами лингвистической переменной "истинность". Правила выполнения нечетких логических операций получают из булевых логических операций с помощью принципа обобщения.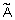 и
и  , а функции принадлежности, задающие истинностные значения этих переменных через
, а функции принадлежности, задающие истинностные значения этих переменных через 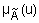 и
и 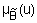 ,
,  . Нечеткие логические операции И (
. Нечеткие логические операции И ( ) и импликация (
) и импликация (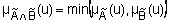 ;
;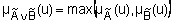 ;
; ;
; .
.

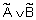
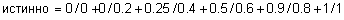 ;
; ;
; .
.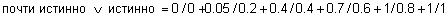 .
. .
.


