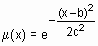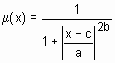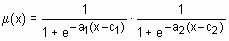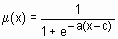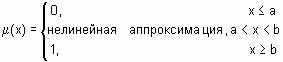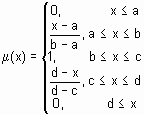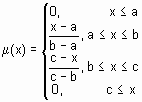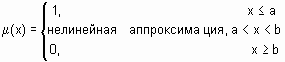Структура fis-файла

Системы нечеткого логического вывода сохраняется на диске в виде fis-файлов - текстовых файлов специального формата. Функции readfis и writefis используются для чтения и записи этих файлов. Иногда удобно модифицировать системы нечеткого логического вывода путем редактирования их fis-файлов, без вызова GUI -модулей Fuzzy Logic Toolbox. Для изменения fis-файлов можно использовать любой текстовый редактор. Однако редактировать fis-файлы надо осторожно так как, изменения некоторых строчек файла влечет за собой необходимость корректирования нескольких других. Например, если при редактировании удален терм, используемый для лингвистической оценки входной или выходной переменной, то необходимо убедиться, что в базе знаний отсутствуют правила, включающие этой терм.

Формат fis-файла описан в табл. 5.1 на примере файла tipper.fis - демонстрационной системы нечеткого логического вывода, определяющей размер чаевых в ресторане. Обратим внимание, что правила базы знаний представлены в индексном формате.

Таблица 5.1 - Формат fis - файла (на примере файла tipper.fis)

Строки файла	Описание
% $ Revision: 1.1 $	строка комментария
[System]	указатель, на начало описания общих параметров системы нечеткого логического вывода
Name='tipper'	наименование системы
Type='mamdani'	тип системы нечеткого логического вывода
NumInputs=2	количество входных переменных системы
NumOutputs=1	количество выходных переменных системы
NumRules=3	количество правил в базе знаний
AndMethod='min'	реализация логической операции И
OrMethod='max'	реализация логической операции ИЛИ
ImpMethod='min'	реализация операции импликации
AggMethod='max'	реализация операции аггреатирования
DefuzzMethod='centroid'	метод дефаззификации
[Input1]	указатель, на начало описания первой входной переменной
Name='service'	наименование первой входной переменной
Range=[0 10]	диапазон изменения
NumMFs=3	количество термов
MF1='poor':'gaussmf',[1.5 0]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='good':'gaussmf',[1.5 5]	наименование второго терма, тип функции принадлежности и ее параметры
MF3='excellent':'gaussmf',[1.5 10]	наименование второго терма, тип функции принадлежности и ее параметры
[Input2]	указатель, на начало описания второй входной переменной
Name='food'	наименование второй входной переменной
Range=[0 10]	диапазон изменения
NumMFs=2	количество термов
MF1='rancid':'trapmf',[0 0 1 3]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='delicious':'trapmf',[7 9 10 10]	наименование второго терма, тип функции принадлежности и ее параметры
[Output1]	указатель, на начало описания первой выходной переменной
Name='tip'	наименование выходной переменной
Range=[0 30]	диапазон изменения
NumMFs=3	количество термов
MF1='cheap':'trimf',[0 5 10]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='average':'trimf',[10 15 20]	наименование второго терма, тип функции принадлежности и ее параметры
MF3='generous':'trimf',[20 25 30]	наименование второго терма, тип функции принадлежности и ее параметры
[Rules]	указатель, на начало описания правил базы знаний
1 1, 1 (1): 2 2 0, 2 (1): 1 3 2, 3 (1): 2	правила базы знаний в индексном формате

В оглавление книги \ К следующему разделу \ К предыдущему разделу

Fuzzy Logic Toolbox включает 11 встроенных функций принадлежностей, которые используют следующие основные функции:

• кусочно-линейную;
• гауссовское распределение;
• сигмоидную кривую;
• квадратическую и кубические кривые.

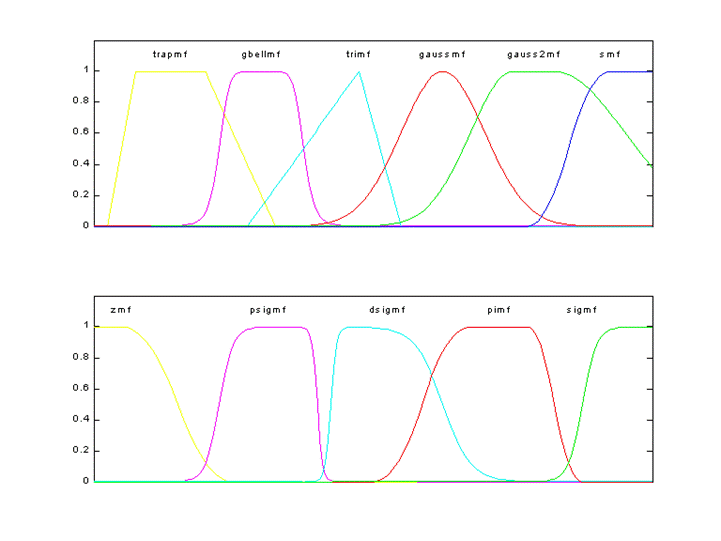
Для удобства имена всех встроенных функций принадлежности оканчиваютя на mf. Вызов функции принадлежности осуществляется следующим образом:

namemf(x, params),

где namemf – наименование функции принадлежности;
x – вектор, для координат которого необходимо рассчитать значения функции принадлежности;
params – вектор параметров функции принадлежности.

Простейшие функции принадлежности треугольная (trimf) и трапециевидная (trapmf) формируется с использованием кусочно-линейной аппроксимации. Трапециевидная функция принадлежности является обобщение треугольной, она позволяет задавать ядро нечеткого множества в виде интервала. В случае трапециевидной функции принадлежности возможна следующая удобная интерпретация: ядро нечеткого множества – оптимистическая оценка; носитель нечеткого множества – пессимистическая оценка.

Две функции принадлежности – симметричная гауссовская (gaussmf) и двухстороняя гауссовская (gaussmf) формируется с использованием гауссовского распределения. Функция gaussmf позволяет задавать ассиметричные функция принадлежности. Обобщенная колоколообразная функция принадлежности (gbellmf) по своей форме похожа на гауссовские. Эти функции принадлежности часто используются в нечетких системах, так как на всей области определения они является гладкими и принимают ненулевые значения.

Функции принадлежности sigmf, dsigmf, psigmf основаны на использовании сигмоидной кривой. Эти функции позволяют формировать функции принадлежности, значения которых начиная с некоторого значения аргумента и до + (-) равны 1. Такие функции удобны для задания лингвистических термов типа “высокий” или “низкий”.

Полиномиальная аппроксимация применяется при формировании функций zmf, pimf и smf, графические изображения которых похожи на функции sigmf, dsigmf, psigmf, соответственно.

Основная информация о встроенных функциях принадлежности сведена в табл. 6.1. На рис. 6.1 приведены графические изображения функций принадлежности, полученные с помощью демонстрационной сценария mfdemo. Как видно из рисунка, встроенные функции принадлежности позволяют задавать разнообразные нечеткие множества.

В Fuzzy Logic Toolbox предусмотрена возможность для пользователя создания собственной функции принадлежности. Для этого необходимо создать m -функцию, содержащую два входных аргумента – вектор, для координат которого необходимо рассчитать значения функции принадлежности и вектор параметров функции принадлежности. Выходным аргументом функции должен быть вектор степеней принадлежности. Ниже приведена m -функция, реализующая колоколообразную функцию принадлежности :

function mu=bellmf(x, params)
%bellmf – bell membership function;
%x – input vector;
%params(1) – concentration coefficient (>0);
%params(2) – coordinate of maximuma.
a=params(1);
b=params(2);
mu=1./(1+ ((x-b)/a).^2);

Рисунок 6.1. Встроенные функции принадлежности

Таблица 6.1. Функции принадлежности

Наименование функции	Описание	Аналитическая формула	Порядок параметров
dsigmf	функция принадлежности в виде разности между двумя сигмоидными функциями		[a1 c1 a2 c2]
gauss2mf	двухсторонняя гауссовская функция принадлежности	если c1<c2, то ; если c1>c2, то .	[a1 c1 a2 c2]
gaussmf	симметричная гауссовская функция принадлежности		[c b]
gbellmf	обобщенная колокообразная функция принадлежности		[a b c]
pimf	пи-подобная функция принадлежности	произведение smf и zmf функций	[a b c d] [a d] – носитель нечеткого множества; [b c] – ядро нечеткого множества;
psigmf	произведение двух сигмоидных функций принадлежности		[a1 c1 a2 c2]
sigmf	сигмоидная функция принадлежности		[a c]
smf	s-подобная функция принадлежности		[a, b]
trapmf	трапециевидная функция принадлежности		[a, b, c, d]
trimf	треугольная функция принадлежности		[a, b, c]
zmf	z-подобная функция принадлежности		[a, b]