Fismain fis_in mam21.fis > fis_out
Примечание: Символ % набирать не следует - это знак-приглашение операционной системы UNIX. Синтаксис fismain подобен mex-файлу, содержащему evalfis.m, за исключением того, что все матрицы и структуры заменяются на имена файлов. В результате выполнения программы появится файл fis_out, содержащий результаты нечеткого логического вывода. Файл представляют собой матрицу размером 121х1, каждая строчка которой соответствует результату нечеткого логического вывода для одного входного вектора. Для сравнения результатов нечетких логических выводов, выполняемых матлабовским mex-файлом и программой fismain, выполним в среде MatLab следующий сценарий: fis = readfis (‘mam21’); В результате получим значение максимального абсолютного отклонения между результатами нечетких логических выводов. Значение отклонения имеет порядок 10 -13. Оно может отличаться в зависимости аппаратных средств – длины разрядной сетки. При использовании Си-кода машины нечеткого логического вывода необходимо помнить, что:
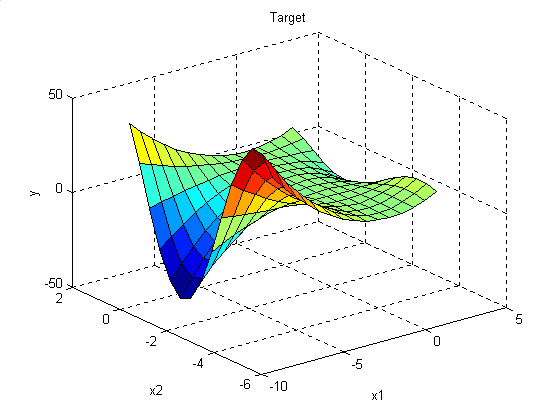
Модуль fuzzy позволяет строит нечеткие системы двух типов - Мамдани и Сугэно. В системах типа Мамдани база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=высокий”. В системах типа Сугэно база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=a0+a1x1+a2x2";. Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний. В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных. 3.1. Проектирование систем типа Мамдани Рассмотрим основные этапы проектирования систем типа Мамдани на примере создания системы нечеткого логического вывода, моделирующей зависимость Для построения трехмерного изображения функции %Построение графика функции y=x1^2*sin(x2-1) В результате выполнения программы получим графическое изображение, приведенное на рис. 3.1. Проектирование системы нечеткого логического вывода, соответствующей приведенному графику, состоит в выполнении следующей последовательности шагов.
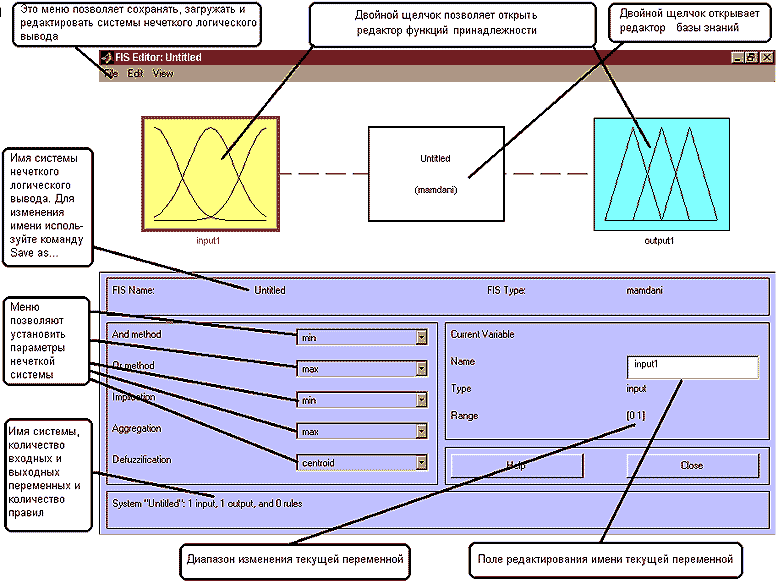
Рис.3.1. Эталонная поверхность Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке. После этого откроется нового графическое окно, показанное на рис. 3.2.
Рис.3.2. Окно редактора FIS-Editor Шаг 2. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input. Шаг 3. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 4. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 5. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 6. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и вводим имя файла, например, first. Шаг 7. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1. Шаг 8. Зададим диапазон изменения переменной x1. Для этого напечатаем -7 3 в поле Range (см. рис. 3.3) и нажмем <Enter>;. Шаг 9. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности. Для этого в меню Edit выберем команду Add MFs... В результате появиться диалоговое окно выбора типа и количества функций принадлежностей. По умолчанию это 3 терма с треугольными функциями принадлежности. Поэтому просто нажимаем <Enter>;. Шаг 10. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис. 3.3). Затем вводим наименование терма, например, Низкий, в поле Name и нажмем <Enter>;. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма, например, Средний, в поле Name и нажмем <Enter>;. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма, например, Высокий, в поле Name и нажмем <Enter>;. В результате получим графическое окно, изображенное на рис. 3.3.
Рис.3.3. Функции принадлежности переменной x1 Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 5 термов с гауссовскими функциями принадлежности. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем -4.4 1.7 в поле Range (см. рис. 3.4) и нажмем <Enter>;. Затем в меню Edit выберем команду Add MFs.... В появившимся диалоговом окне выбираем тип функции принадлежности gaussmf в поле MF type и 5 термов в поле Number of MFs. После этого нажимаем <Enter>;.
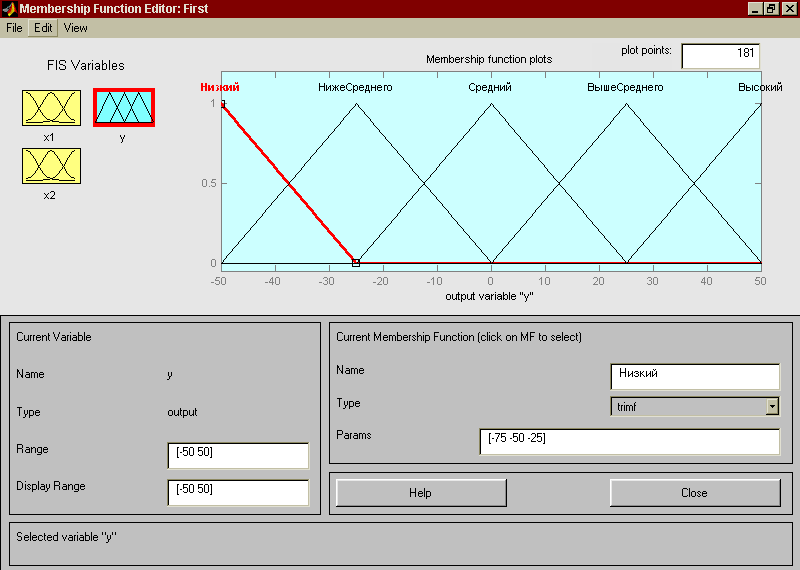
Рис 3.4. Функции принадлежности переменной x2 Шаг 12. По аналогии с шагом 10 зададим следующие наименования термов переменной x2: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рис. 3.4. Шаг 13. Зададим функции принадлежности переменной y. Для лингвистической оценки этой переменной будем использовать 5 термов с треугольными функциями принадлежности. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. Зададим диапазон изменения переменной y. Для этого напечатаем -50 50 в поле Range (см. рис. 3.5) и нажмем <Enter>;.Затем в меню Edit выберем команду Add MFs.... В появившимся диалоговом окне выбираем 5 термов в поле Number of MFs. После этого нажимаем <Enter>;.
Рис 3.5. Функции принадлежности переменной y Шаг 14. По аналогии с шагом 10 зададим следующие наименования термов переменной y: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рис. 3.5. Шаг 15. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit выберем команду Edit rules.... Шаг 16. На основе визуального наблюдения за графиком, изображенным на рис. 3.1 сформулируем следующие девять правил:
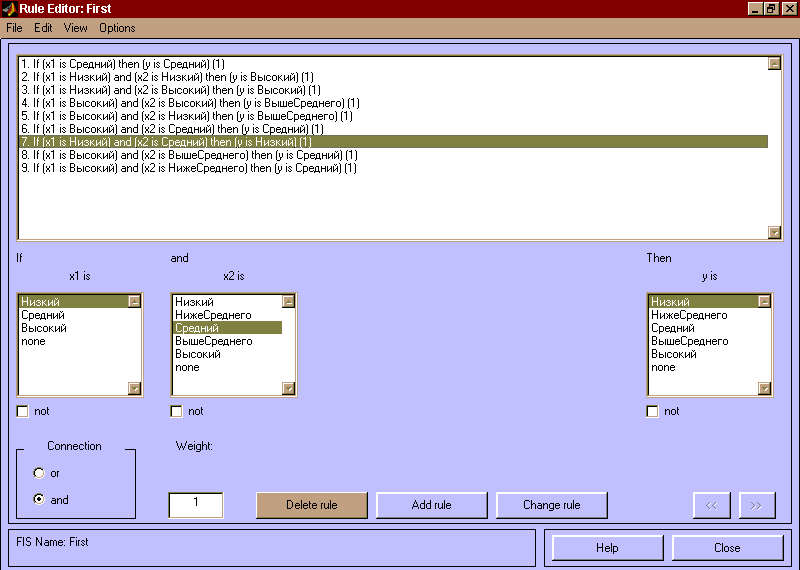
Для ввода правила необходимо выбрать в меню соответствующую комбинацию термов и нажать кнопку Add rule. На рис. 3.6 изображено окно редактора базы знаний после ввода всех девяти правил. Число, приведенное в скобках в конце каждого правила представляет собой весовым коэффициент соответствующего правила.
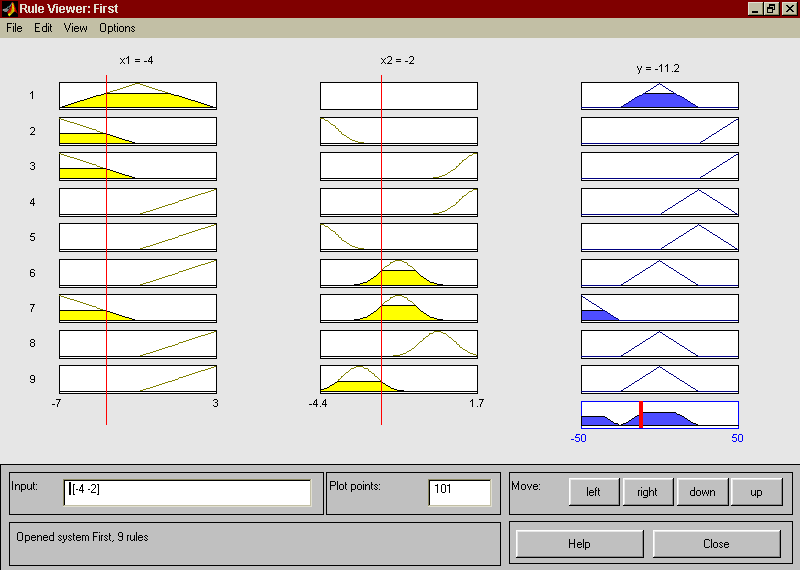
Рис 3.6. База знаний в RuleEditor Шаг 17. Сохраним созданную систему. Для этого в меню File выбираем в подменю Export команду To disk. На рис. 3.7 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод.
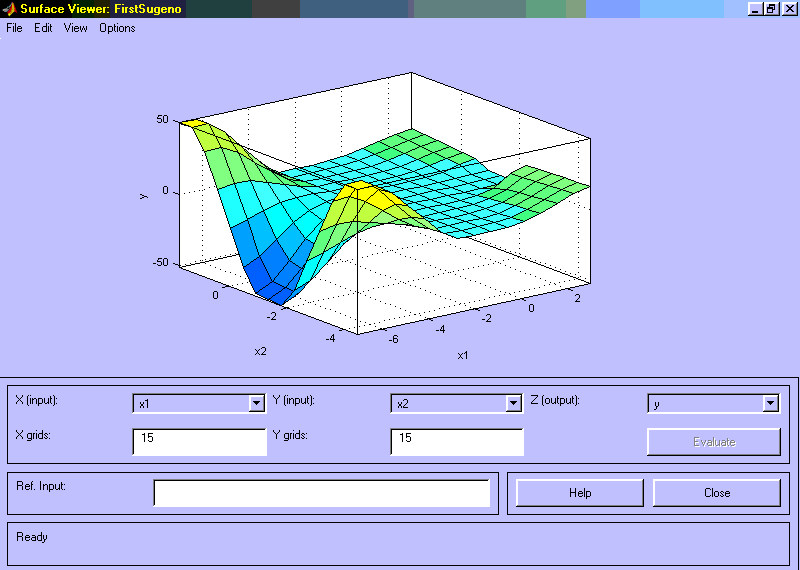
Рис 3.7. Визуализация нечеткого логического вывода в RuleViewer На рис. 3.8 приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View. Сравнивая поверхности на рис. 3.1 и на рис. 3.8 можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость.
Рис 3.8. Поверхность “входы-выход” в окне SurfaceViwer 3.2. Проектирование систем типа Сугэно Рассмотрим основные этапы проектирования систем типа Сугэно на примере создания системы нечеткого логического вывода, моделирующей зависимость
Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов. Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке. После этого откроется нового графическое окно, показанное на рис. 3.2. Шаг 2. Выберем тип системы. Для этого в меню File выбираем в подменю New fis… команду Sugeno. Шаг 3. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input. Шаг 4. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 5. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 6. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>;. Шаг 7. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и введем имя файла, например, FirstSugeno. Шаг 8. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1. Шаг 9. Зададим диапазон изменения переменной x1. Для этого напечатаем -7 3 в поле Range (см. рис. 3.9) и нажмем <Enter>;.
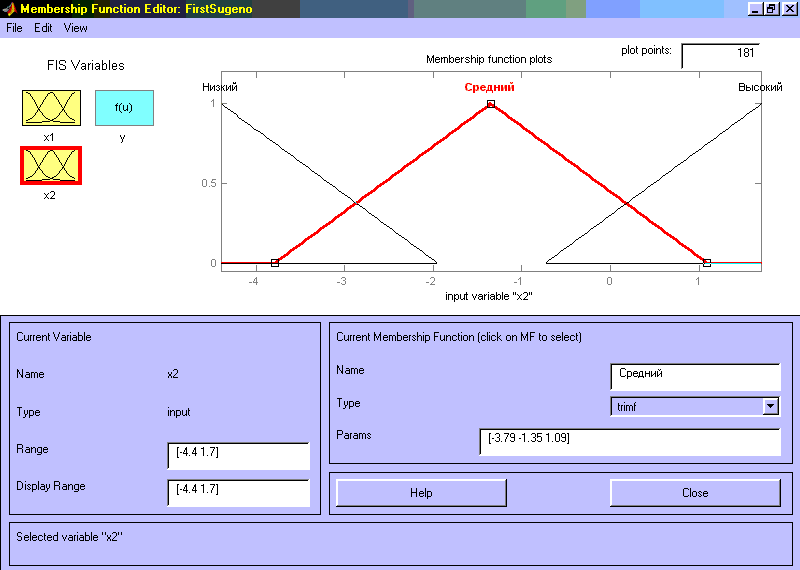
Рис 3.9. Функции принадлежности переменной x1 Шаг 10. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать, 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис. 3.9). Затем напечатаем наименование терма Низкий в поле Name. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма Средний в поле Name. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма Высокий в поле Name и нажмем <Enter>;. В результате получим графическое окно, изображенное на рис. 3.9. Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем -4.4 1.7 в поле Range (см. рис. 3.10) и нажмем <Enter>;. По аналогии с предыдущим шагомзададим следующие наименования термов переменной x2: Низкий, Средний, Высокий. В результате получим графическое окно, изображенное на рис. 3.10.
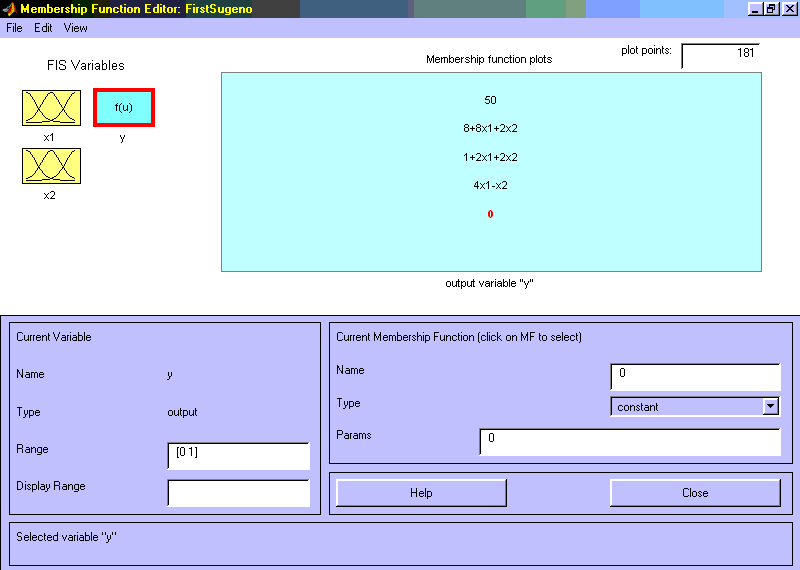
Рис 3.10. Функции принадлежности переменной x2 Шаг 12. Зададим линейные зависимости между входами и выходом, приведенные в базе знаний. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. В правом верхнем угле появилось обозначение трех функций принадлежности, каждая из которых соответствует одной линейной зависимости между входами и выходам. В базе знаний, приведенной в начале подраздела 3.2 указаны 5 различных зависимостей: y=50; y=4x1-x2; y=2x1+2x2+1; y=8x1+2x2+8; y=0. Поэтому добавим еще две зависимости путем выбора команды Add Mfs… меню Edit. В появившимся диалоговом окне в поле Number of MFs выбираем 2 и нажимаем кнопку OK. Шаг 13. Зададим наименования и параметры линейных зависимостей. Для этого делаем один щелчок левой кнопкой мыши по наименованию первой зависимости mf1. Затем печатаем наименование зависимости, например 50, в поле Name, и устанавливаем тип зависимости – константа путем выбора опции Сonstant в меню Type. После этого вводим значение параметра – 50 в поле Params. Аналогично для второй зависимости mf2 введем наименование зависимости, например 8+8x1+2x2. Затем укажем линейный тип зависимости путем выбора опции Linear в меню Type и введем параметры зависимости 8 2 8 в поле Params. Для линейной зависимости порядок параметров следующий: первый параметр – коэффициент при первой переменной, второй – при второй и т.д., и последний параметр – свободный член зависимости. Аналогично для третьей зависимости mf3 введем наименование зависимости, например 1+2x1+2x2, укажем линейный тип зависимости и введем параметры зависимости 2 2 1. Для четвертой зависимости mf4 введем наименование зависимости, например 4x1-x2, укажем линейный тип зависимости и введем параметры зависимости 4 -1 0. Для пятой зависимости mf5 введем наименование зависимости, например 0, укажем тип зависимости - константа и введем параметр зависимости 0. В результате получим графическое окно, изображенное на рис. 3.11.
Рис 3.11. Окно линейных зависимостей “входы-выход” Шаг 14. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit команду Edit rules.... и введем правила базы знаний. Для ввода правила необходимо выбрать соответствующую комбинацию термов и зависимостей и нажать кнопку Add rule. На рис. 3.12 изображено окно редактора базы знаний после ввода всех шести правил.
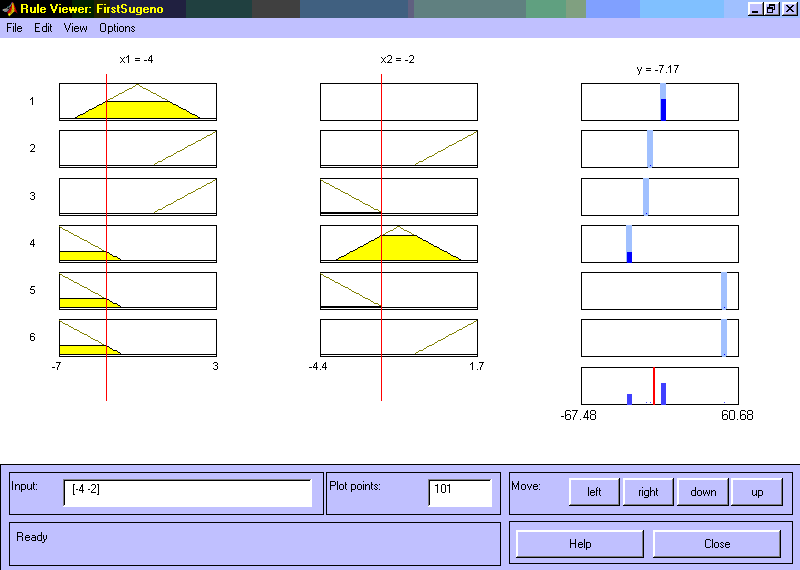
Рис 3.12. Нечеткая база знаний для системы типа Сугэно На рис. 3.13 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод. Как видно из этого рисунка значение выходной переменной рассчитывается как среднее взвешенное значение результатов вывода по каждому правилу.
Рис. 3.13 Визуализация нечеткого логического вывода для системы типа Сугэно На рис. 3.14 приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View. Сравнивая поверхности на рис. 3.1, рис. 3.8 и на рис. 3.14 можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость. При этом, модель типа Сугэно более точная. Преимущество моделей типа Мамдани состоит в том, что правила базы знаний являются прозрачными и интуитивно понятными, тогда как для моделей типа Сугэно не всегда ясно какие линейные зависимости “входы-выход” необходимо использовать.
Рис 3.14. Поверхность “входы-выход” для системы типа Сугэно В настоящем разделе описана система прогнозирования результатов футбольных матчей, в основу которой положены формализованные в виде нечеткой базы знаний лингвистические высказывания правила типа “Если – То”. Система разработана в Винницком государственном техническом университет доцентом Штовбой С.Д. и студентом 5-го курса Вивдюком В.В. Для настройки и тестирования системы использовались данные о матчах чемпионатов Украины по футболу 2000 -2002 годов. Для запуска системы необходимо ввести команду fuzzy football. [Fis-файл системы football.fis] Нами отобраны следующие факторы, которые оказывают наибольшее влияние на результат поединка:
Заметим, что значения этих факторов легко может быть определено до начала футбольного матча. Результата матча (y) прогнозируется как разница голов забитых командой хозяином поля и гостевой командой. Для лингвистической оценки входных и выходной переменных используются следующие терм-множества:
Экспертные лингвистические высказывания, отражающие взаимосвязь между факторами х1-x5 и результатом футбольного матча (y) представлены в табл. 4.1. Каждая строка таблицы соответствует одному правилу, например, для первой строки это правило: Если x1=”Большая_скамейка” и х2=”Преимущественно_выигрыш” и х3=”Лидер” и х4=”Абсолютное_преимущество” и х5=”Разгромные_встречи”, То y=”Крупный_выигрыш”. Таблица 4.1. База знаний
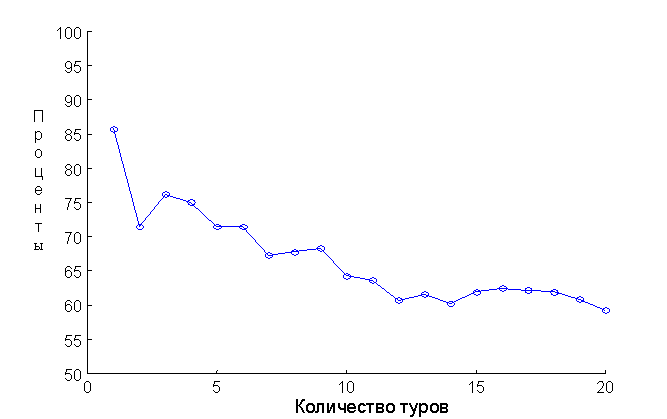
Тестирование нечеткой модели на выборке из 175 матчей показывает, что среднеквадратическое отклонение составляет 1.60, при этом статистическая оценка вероятности правильного предсказания исхода поединка (выигрыш, ничья, проигрыш) составляет 0.64. Проиллюстрируем возможности предложенной нечеткой системы на примере прогнозирования результатов 9-го чемпионата Украины. Исходной информацией, необходимой для прогнозирования служат результаты игр за 1-8 чемпионаты и результаты первых пяти игр 9-го чемпионата. На основе этой информации необходимо спрогнозировать результаты оставшихся 6, 7,...., 26 туров. В каждом туре происходит 7 матчей, поэтому необходимо спрогнозировать результаты 21*7=147 игр. Прогнозирование проводилось по следующей методике. Вначале спрогнозируем результаты 6-го тура. Затем с учетом полученных данных пересчитаем значения факторов x2-x5 и спрогнозируем результаты 7-го тура, потом 8-го и т.д. по 26 тур. Заметим, что значение фактора x5 - “встреча команд”, необходимо пересчитывать только со второго круга чемпионата, т.е. начиная с 14-го тура. Значение фактора x1 на i-ом туре определим как x1(i)=x1(6)/(i-5), где x1(6) - значения фактора x1 в 6-м туре. Это позволит снизить влияние этого фактора при моделировании последних туров, т.к. на момент прогнозирования количество травмированных и дисквалифицированных игроков является величиной неизвестной. Результаты прогнозирования в виде зависимости точности прогнозирования от количества туров и в виде итоговой таблицы чемпионата показаны на рис.4.1 и в табл. 4.2, соответственно.
Рис. 4.1 – Зависимость точности прогнозирования от количества туров Таблица 4.2 - Результирующая турнирная таблица
|
, 
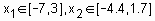. Проектирование системы нечеткого логического вывода будем проводить на основе графического изображения указанной зависимости.
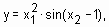в области 
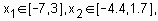составим следующую программу:
