Математический аппарат
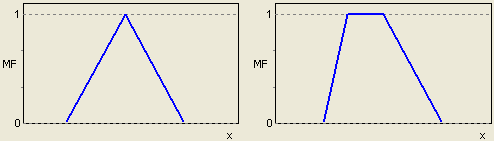
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) Проиллюстрируем это на простом примере. Формализуем неточное определение 'горячий чай'. В качестве x (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяется от 0 до 100 градусов. Нечеткое множество для понятия 'горячий чай' может выглядеть следующим образом: C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}. Так, чай с температурой 60 С принадлежит к множеству 'Горячий' со степенью принадлежности 0,80. Для одного человека чай при температуре 60 С может оказаться горячим, для другого – не слишком горячим. Именно в этом и проявляется нечеткость задания соответствующего множества. Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение. Пересечение двух нечетких множеств (нечеткое "И"): A В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения – наиболее распространенные случаи t-нормы и t-конормы. Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных. Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X. названия; множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных; универсального множества X; синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка; семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X. Рассмотрим такое нечеткое понятие как 'Цена акции'. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: 'Низкая', 'Умеренная', 'Высокая' и зададим область рассуждений в виде X=[100;200] (единиц). Последнее, что осталось сделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T. Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности. Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c). Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
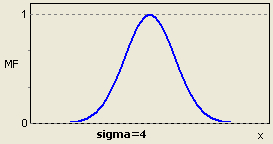
Функция принадлежности гауссова типа описывается формулой
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр
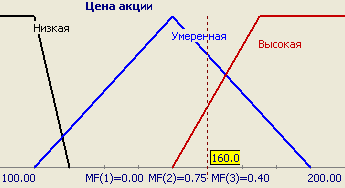
Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике. На рисунке 3 приведен пример описанной выше лингвистической переменной 'Цена акции', на рисунке 4 – формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности к множеству 'Молодой' равна 0, 'Средний' – 0,47, 'Выше среднего' – 0,20.
Количество термов в лингвистической переменной редко превышает 7.
|

 [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
[0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность. B: MFAB(x)=min(MFA(x), MFB(x)).
B: MFAB(x)=min(MFA(x), MFB(x)). 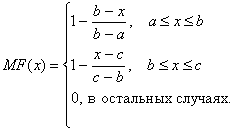
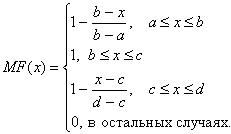
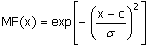
 отвечает за крутизну функции.
отвечает за крутизну функции.