Часть 1. Определение сопротивления с помощью модели мостика Уитстона
Министерство образования РФ Тамбовский государственный технический университет
Кафедра физики
Лабораторная работа
Определение сопротивления с помощью мостика Уитстона»
Тамбов 2002
21.03.02
Определение сопротивления с помощью мостика Уитстона Цель работы: ознакомление с принципом работы измерительной мостовой схемы и экспериментальное определение величины неизвестного сопротивления Приборы и принадлежности: источник постоянной ЭДС, магазин сопротивлений, неизвестные сопротивления, реохорд, гальванометр, ключ.Мост постоянного тока типа ММВ. Авометр любого типа.
Часть 1. Определение сопротивления с помощью модели мостика Уитстона
Методические указания и описание установки Одним из наиболее точных способов измерения сопротивлений является метод мостика Уитстона. Принципиальная схема представляет собой замкнутый прямоугольник, образованный сопротивлениями R 1, R 2, R 3, R 4 (рис.1). В диагональ АС подсоединяется источник постоянного тока
Где Это означает, что потенциалы точек В и D одинаковы, т.е.
.Рис.1 . Токи, текущие через сопротивления
При условии
Уравнения (5) и (6) называются уравнениями сбалансированного моста. Для последовательно включённых сопротивлений
В настоящей работе используется установка, электрическая схема которой показана на рис.2. Сопротивление
Рис.2. Т.к. сопротивление однородного цилиндрического проводника
В итоге, уравнение (7) для расчёта неизвестного сопротивления (R x) принимает окончательный вид:
Порядок выполнения работы.
1. В плечо АВ (рис.2) включите одно из двух заданных преподавателем неизвестных сопротивлений Rxi, Rxj. Движок реохорда поставьте так, чтобы он находился в средней трети длины реохорда. Замкните ключ К нажав кнопку и вращением соответствующих декад (исключая Х10000) магазина сопротивлений Rm, добейтесь того, чтобы стрелка гальванометра не зашкаливала ни вправо, ни влево и легко выводилась на ноль. В таблицу 1 запишите значения l 1 и l 2 и величину сопротивления, установленного на магазине сопротивлений R m. 2. Измените сопротивление магазина Rm на 10% от первоначального значения. Передвигая движок реохорда, при нажатой кнопке ключа, вновь добейтесь нулевого тока в цепи гальванометра и занесите новые значения l 1, l 2 и R m в таблицу 1. Проделайте 5 таких измерений, изменяя каждый раз сопротивление магазина R m на 10 % от предыдущего значения. 3. В этой же последовательности произведите измерения второго неизвестного сопротивления Rxj, а затем величины общих сопротивлений Rxi Rxjпосл и RxiRxjпар при последовательном и параллельном соединении сопротивлений Rxi и Rxj. Данные занесите в таблицы 2,3, и 4. 4. По формуле (9), используя результаты измерений, рассчитайте по пять значений сопротивлений Rxi и Rxj и найдите их средние значения (Rхiср) и (Rхjср). 5. По формуле (9) аналогично рассчитайте по 5 значений общих сопротивлений RxiRxj. при последовательном и параллельном соединении сопротивлений Rxi и Rxj. Найдите их средние значения. 6. Вычислите абсолютные погрешности Δ Rxi и Δ Rxj для каждого искомого сопротивления, а также абсолютные ошибки общих сопротивлений при последовательном и параллельном включении сопротивлений Rxi и Rxj. Рассчитайте среднюю абсолютную погрешность для каждого неизвестного сопротивления и среднюю абсолютную погрешность общих сопротивлений при последовательном и параллельном соединении сопротивлений Rxi и Rxj. 7. По найденным средним величинам сопротивлений и средним значениям их абсолютных ошибок, рассчитайте для каждого случая относительные погрешности Е.
Таблица 1
Таблица 2
Таблица 3
Таблица 4
8. Сравните экспериментально полученные значения общих сопротивлений в таблицах 3 и 4 с теоретическими, рассчитываемыми при последовательном и параллельном соединении резисторов Rxi и Rxj. Контрольные вопросы 1. Нарисуйте схему мостика Уитстона и объясните принцип его действия. 2. Выведите расчётную формулу (9). 3. Напишите и объясните законы Ома для однородного, неоднородного участков и полной цепи. 4. Объясните физический смысл закона Ома в дифференциальной форме. 5. Зависит ли погрешность измерений от положения движка реохорда.
Литература 1. Ахматов А.С., Андреевский В.М. и др. Лабораторный практикум по физике. –М. Высшая школа, 1980. 2. Гольдин Л.Л. и др. Руководство к лабораторным занятиям по физике. –М. Наука. 1973. 3. Детлаф А.А., Яворский Б.М. Курс физики. – М. Высшая школа, 1989. Т.2.
|

 , а в BD, образующую “мост”, нуль-гальванометр G. Сопротивления R 1, R 2, R 3, R 4 называются плечами моста. При произвольно выбранных сопротивлениях R 1, R 2, R 3, R 4 в диагонали BD будет идти ток, вызывающий отклонение стрелки гальванометра в ту или другую сторону. Величина этого тока определяется по закону Ома:
, а в BD, образующую “мост”, нуль-гальванометр G. Сопротивления R 1, R 2, R 3, R 4 называются плечами моста. При произвольно выбранных сопротивлениях R 1, R 2, R 3, R 4 в диагонали BD будет идти ток, вызывающий отклонение стрелки гальванометра в ту или другую сторону. Величина этого тока определяется по закону Ома: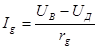 ,
, и
и  – потенциалы в точках В и D,
– потенциалы в точках В и D,  - сопротивление гальванометра. Подбирая определенные соотношения сопротивлений
- сопротивление гальванометра. Подбирая определенные соотношения сопротивлений 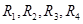 можно добиться отсутствия тока в цепи гальванометра (
можно добиться отсутствия тока в цепи гальванометра (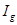 = 0).
= 0). . В этом случае мост называют сбалансированным
. В этом случае мост называют сбалансированным
 . Для нахождения этих соотношений запишем закон Ома для каждого из участков цепи через разности потенциалов на концах соответствующих сопротивлений:
. Для нахождения этих соотношений запишем закон Ома для каждого из участков цепи через разности потенциалов на концах соответствующих сопротивлений: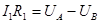 (1)
(1)  (3)
(3) (2)
(2) 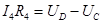 (4)
(4)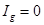 , когда
, когда  , в уравнениях (1), (2) и (3), (4) правые части равны, следовательно, равны и левые части:
, в уравнениях (1), (2) и (3), (4) правые части равны, следовательно, равны и левые части: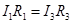 (5)
(5)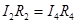
 и
и 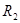 ,
,  и
и 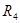 и отсутствия тока в диагонали BD, имеем
и отсутствия тока в диагонали BD, имеем  и
и  . Разделив почленно уравнение (5) на (6) получаем:
. Разделив почленно уравнение (5) на (6) получаем: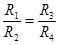 , откуда, например,
, откуда, например, (7)
(7)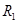 заменено неизвестным сопротивлением
заменено неизвестным сопротивлением  , величину которого нужно определить; вместо постоянного резистора R 2 включен магазин сопротивлений R m, позволяющий менять значение этого сопротивления в широком диапазоне; сопротивления R3 и R 4 заменены единой эталонированной проволокой ADC (ее сечение одинаково по всей длине) – реохордом. Движок D, перемещаясь по реохорду, меняет плечи мостика R3 и R4.
, величину которого нужно определить; вместо постоянного резистора R 2 включен магазин сопротивлений R m, позволяющий менять значение этого сопротивления в широком диапазоне; сопротивления R3 и R 4 заменены единой эталонированной проволокой ADC (ее сечение одинаково по всей длине) – реохордом. Движок D, перемещаясь по реохорду, меняет плечи мостика R3 и R4.







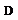















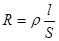 , где r – удельное сопротивление, l – длина и S – сечение проволоки реохорда, при постоянных r и S пропорционально длине l, то отношение сопротивлений R 3 / R 4 в уравнении (7) будет эквивалентно отношению плеч реохорда, т.е.
, где r – удельное сопротивление, l – длина и S – сечение проволоки реохорда, при постоянных r и S пропорционально длине l, то отношение сопротивлений R 3 / R 4 в уравнении (7) будет эквивалентно отношению плеч реохорда, т.е.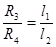 (8)
(8) (9)
(9)


