Уравнение Бернулли для идеальной жидкости
Для получения уравнения Д. Бернулли используем теорему об изменении кинетической энергии (теорему живых сил), которая связывает изменение кинетической энергии системы точек с работой сил, вызывающих это изменение. (см. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики, т2, стр. 242) В интегральной форме эта теорема формулируется следующим образом: «Приращение кинетической энергии системы материальных точек на конечном перемещении равно сумме работ внешних и внутренних сил, действующих на этом перемещении»
Выделим в элементарной струйке в данный момент времени В установившемся движении новый объем будет отличаться от предыдущего только тем, что к нижней части трубки присоединится элементарный объем, заключенный между сечениями
Рисунок 1 – Схема движения объема в трубке тока
Изменение кинетической энергии в рассматриваемом объеме трубки сведется к разности
Массы
так как Замечая, что перемещение частиц в сечениях
Работа сил давления, приложенных к боковой поверхности трубки тока равна нулю, т.к. перемещения жидкости вдоль боковой поверхности трубки тока перпендикулярны к силам давления. Работу сил тяжести получим как уменьшение потенциала при перемещении выделенного объема жидкости из начального положения в конечное. При расчете этого уменьшения потенциала примем во внимание, что потенциал общей части начального и конечного положения объемов при этом выпадает и работа сил тяжести будет равна
Приравнивая, согласно теореме об изменении кинетической энергии выражение
Так как
Полученное выражение называют трехчленом Д. Бернулли.
|

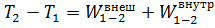
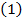
 объем, заключенный между двумя ортогональными к боковой поверхности трубки сечениями
объем, заключенный между двумя ортогональными к боковой поверхности трубки сечениями  и
и 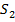 . В смежный момент времени
. В смежный момент времени 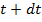 выделенный объем жидкости сместится вдоль трубки тока и займет положение, ограниченное сечениями
выделенный объем жидкости сместится вдоль трубки тока и займет положение, ограниченное сечениями  и
и 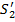 .
.


 и
и  вычисляются с использованием уравнения неразрывности
вычисляются с использованием уравнения неразрывности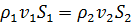
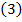
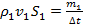 ,
,  , то
, то 
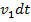 и
и  , составим выражение элементарной работы приложенных к сечениям
, составим выражение элементарной работы приложенных к сечениям 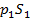 и
и  , в виде
, в виде
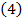
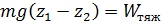
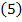
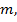 получим
получим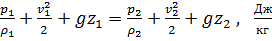
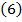
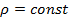 (жидкость не сжимаема), то, поделив на
(жидкость не сжимаема), то, поделив на  левую и правую части неравенства, получим
левую и правую части неравенства, получим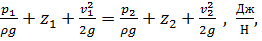 т.е. и ст.ж.
т.е. и ст.ж. , т.е.
, т.е. 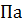 .
. 



