2.1. Уравнение Бернулли для линии тока идеальной жидкости записывается в следующем виде
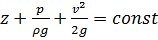 ,
,
откуда для двух любых точек, взятых на одной и той же линии, имеем:
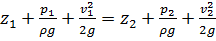
Индексы 1 и 2 означают, что соответствующие величины взяты в точках 1 и 2. Уравнение впервые было получено Даниилом Бернулли в 1738г. с помощью теоремы изменения кинетической энергии, примененной к элементарной струйке.
Уравнение Бернулли является одним из основных уравнений гидромеханики, поэтому дадим истолкование его членов.
2.2. Геометрическое представление членов уравнения Бернулли. Выделим в потоке элементарную струйку, осью которой является линия тока. Геометрические построения выполним для этой линии тока, отметив на ней точки 1 и 2 (рисунок 2). Все члены уравнения Бернулли имеют размерность длины и поэтому могут быть представлены вертикальными отрезками. Первый член  – высотная отметка, или нивелирная высота, представляет собой расстояние по вертикали от рассматриваемой точки до некоторой плоскости
– высотная отметка, или нивелирная высота, представляет собой расстояние по вертикали от рассматриваемой точки до некоторой плоскости  (рисунок 2), которую называют плоскостью сравнения; второй -
(рисунок 2), которую называют плоскостью сравнения; второй -  называют высотой гидродинамического давления, а третий -
называют высотой гидродинамического давления, а третий - 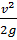 – скоростной высотой. Так как по уравнению Бернулли сумма этих трех членов вдоль линии тока неизменна, то вершины их суммарных отрезков, построенных в точках рассматриваемой линии тока, должны лежать в одной горизонтальной плоскости
– скоростной высотой. Так как по уравнению Бернулли сумма этих трех членов вдоль линии тока неизменна, то вершины их суммарных отрезков, построенных в точках рассматриваемой линии тока, должны лежать в одной горизонтальной плоскости 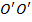 , параллельной плоскости
, параллельной плоскости  (рисунок 2).
(рисунок 2).
2.3. Гидродинамический смыл уравнения Бернулли.
Члены уравнения Бернулли еще называют напорами, так как каждый из них может быть заменен высотой соответствующего столба жидкости. Член 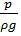 представляет высоту такого столба, который в данной точке линии тока создает давление, равное гидродинамическому давлению
представляет высоту такого столба, который в данной точке линии тока создает давление, равное гидродинамическому давлению  .
.
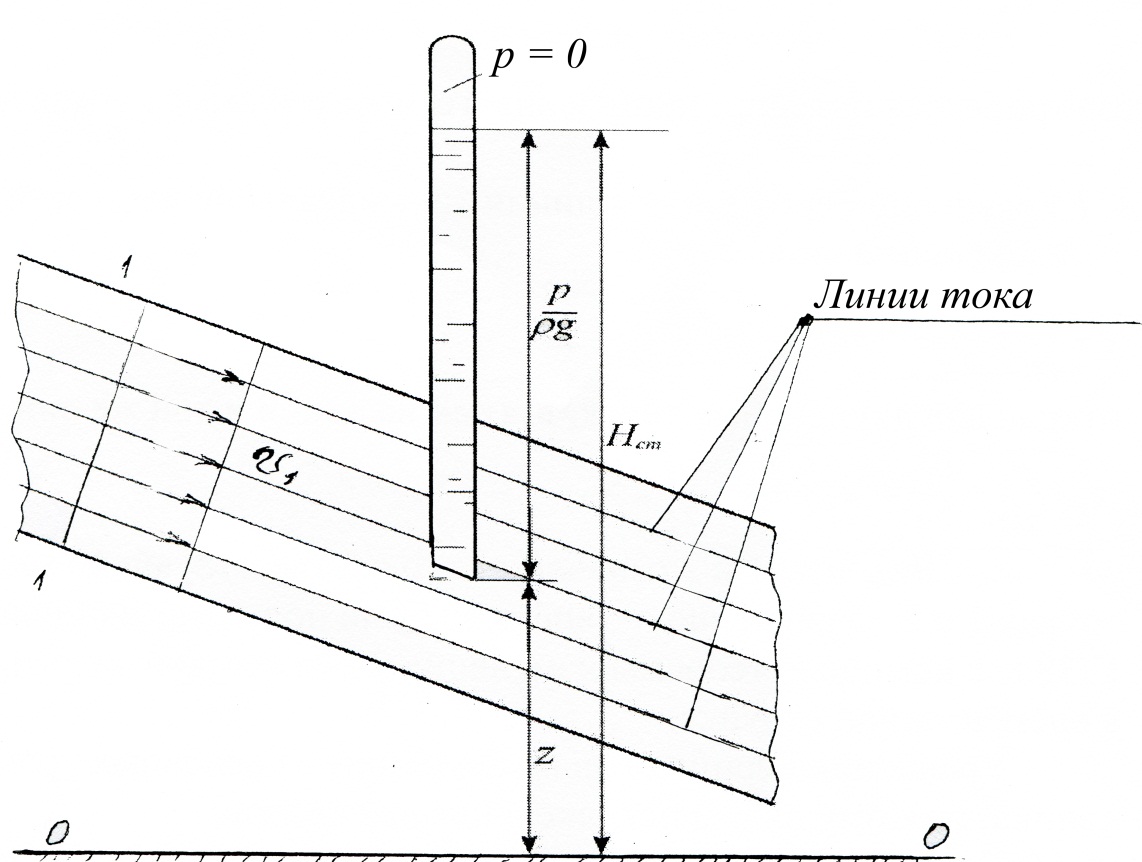
Рисунок 2 – Иллюстрация «напоров» на примере элементарной струйки
Действительно, если опустить в поток трубку с закрытым верхним концом так, чтобы линия тока лежала в плоскости среза нижнего конца этой трубки, то жидкость в ней поднимается на высоту, равную высоте давления  , поэтому
, поэтому 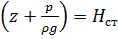 называют статическим напором (рисунок 2).
называют статическим напором (рисунок 2).
Если же в некоторой точке А (рисунок 3) движущейся жидкости, установить две трубки так, что у одной трубки нижний срез параллелен скорости движения в данной точке, а у другой – нижний конец изогнут против течения, то разность между высотами столбов жидкости в этих трубках будет равна скоростной высоте 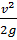 . Действительно, возьмем на линии тока, вдоль которой изогнут нижний конец второй трубки, точку В на некотором удалении от точки А. Тогда согласно уравнению Бернулли
. Действительно, возьмем на линии тока, вдоль которой изогнут нижний конец второй трубки, точку В на некотором удалении от точки А. Тогда согласно уравнению Бернулли
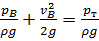 ,
,
где 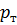 – давление в заторможенной жидкости у загнутого конца трубки. Если же из точки А трубку убрать, то по уравнению Бернулли получим
– давление в заторможенной жидкости у загнутого конца трубки. Если же из точки А трубку убрать, то по уравнению Бернулли получим
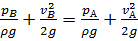 .
.
Отсюда следует, что
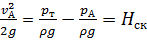
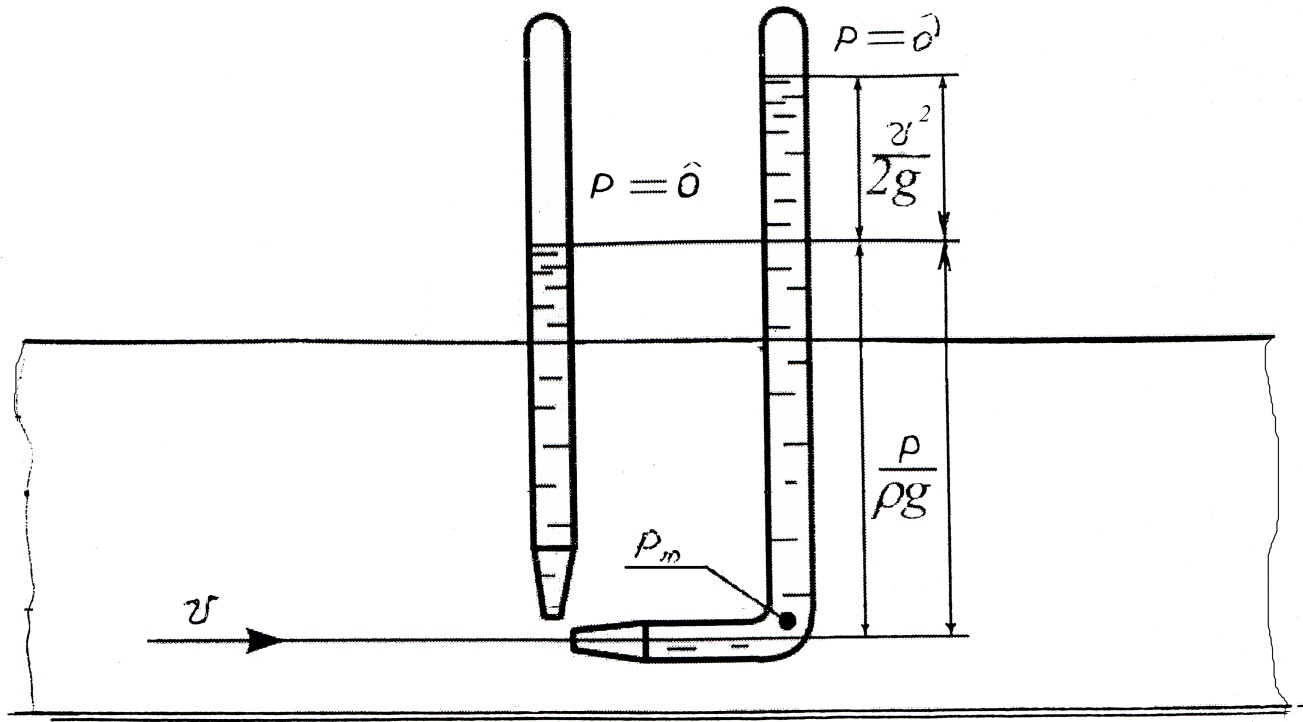
Рисунок 3 – Схема изменения скоростного напора
Величину 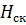 называют скоростным напором. Трубки с загнутым нижним концом, предназначенные для измерения скоростного напора, называют скоростными трубками или трубками Пито.
называют скоростным напором. Трубки с загнутым нижним концом, предназначенные для измерения скоростного напора, называют скоростными трубками или трубками Пито.
Сумма статического напора 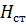 и скоростного напора
и скоростного напора 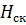 обозначается через
обозначается через 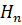
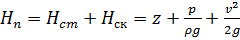
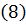
Часто в практических задачах рассматривается не абсолютное давление в точке, а избыточное давление над атмосферным. Тогда вводят понятие избыточного напора:
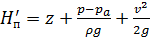 .
.
Таким образом, уравнение Бернулли на линии тока можно представить в виде:
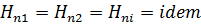 или
или 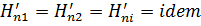
Это значит, что величина гидродинамического напора во всех точках одной и той же линии тока одинакова и напорная линия, т.е. линия, проведенная через верхние концы гидродинамических напоров, лежит в горизонтальной плоскости.
На рисунке 4 след этой плоскости показан линией  . Что касается статического напора
. Что касается статического напора 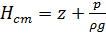 или пьезометрического напора
или пьезометрического напора 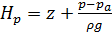 ,
,
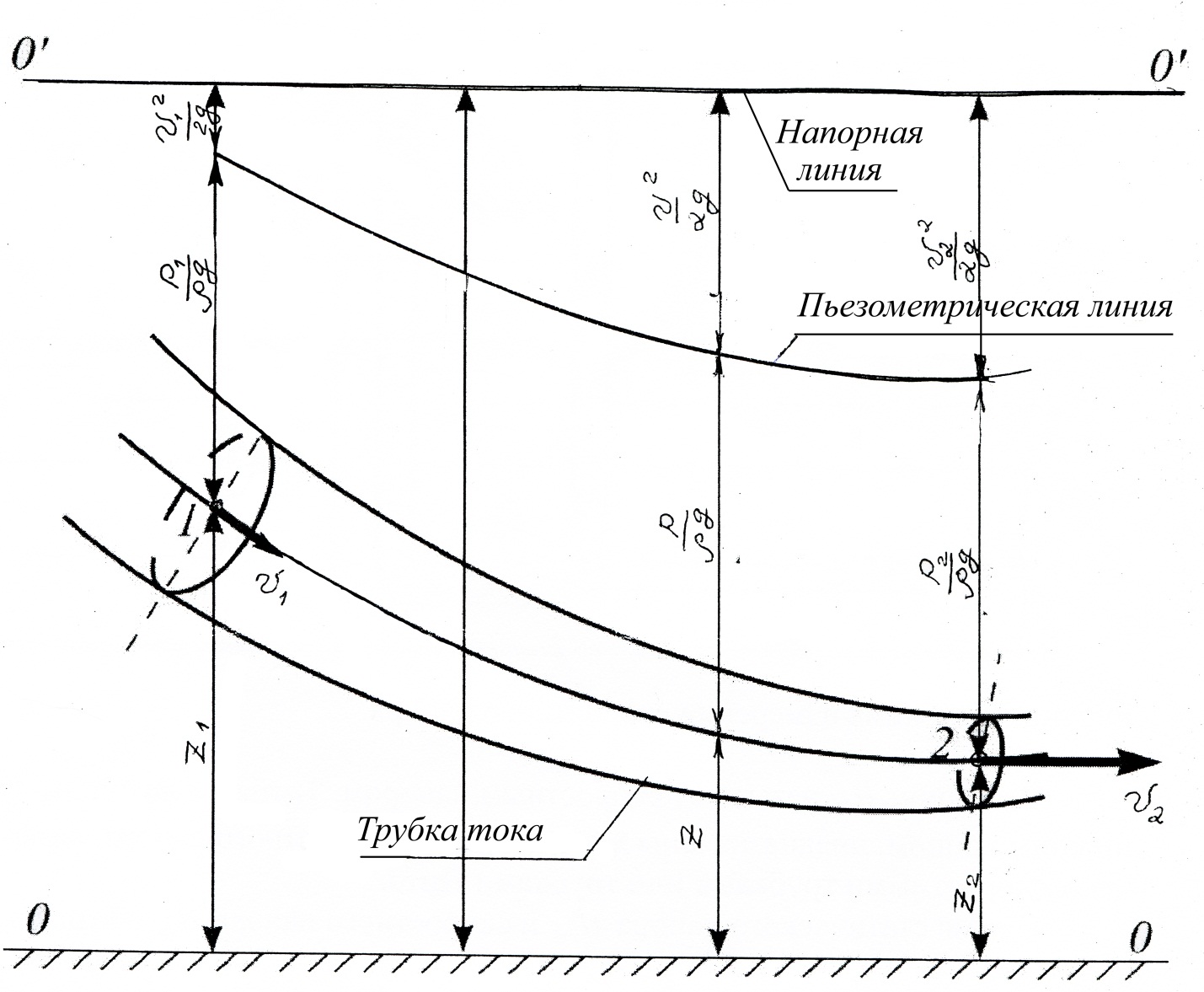
Рисунок 4 – интерпретация слагаемых уравнения Бернулли для идеальной жидкости.
то в общем случае движения эти напоры вдоль линии тока изменяются в зависимости от скоростного напора, который в свою очередь зависит от формы границ потока. В связи с этим вводят понятие статического уклона  или пьезометрического уклона
или пьезометрического уклона  , которые определяются следующим образом:
, которые определяются следующим образом:
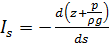 ,
, 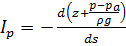 ,
,
где  – элемент длины линии тока.
– элемент длины линии тока.
2.4. Энергетический смысл уравнения Бернулли.
Если 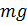 – вес частицы жидкости, то произведение
– вес частицы жидкости, то произведение  будет определять потенциальную энергию этой частицы относительно выбранной плоскости сравнения. Поделив
будет определять потенциальную энергию этой частицы относительно выбранной плоскости сравнения. Поделив  на
на 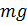 , получим потенциальную энергию положения частицы,
, получим потенциальную энергию положения частицы,
рассчитанную на единицу веса.Рассматривая бесконечно малую частицу жидкости, в пределе получим, что  есть потенциальная энергия положения в точке потока жидкости, рассчитанная на единицу веса.
есть потенциальная энергия положения в точке потока жидкости, рассчитанная на единицу веса.
Умножим теперь  на вес частицы. Произведение
на вес частицы. Произведение 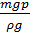 определяет потенциальную энергию давления, испытываемого частицей от окружающей жидкости, так как
определяет потенциальную энергию давления, испытываемого частицей от окружающей жидкости, так как  представляет собой высоту давления. Отношение
представляет собой высоту давления. Отношение 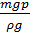 к
к 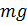 есть потенциальная энергия давления, испытываемого данной частицей, рассчитанная на единицу веса. Выбирая бесконечно малую частицу, в пределе получим, что
есть потенциальная энергия давления, испытываемого данной частицей, рассчитанная на единицу веса. Выбирая бесконечно малую частицу, в пределе получим, что  есть потенциальная энергия давление в рассматриваемой точке потока жидкости. Таким образом, потенциальная энергия в точке потока жидкости, рассчитанная на единицу веса, равна сумме
есть потенциальная энергия давление в рассматриваемой точке потока жидкости. Таким образом, потенциальная энергия в точке потока жидкости, рассчитанная на единицу веса, равна сумме 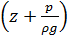 ,
,  представляет собой кинетическую энергию частицы, поэтому для бесконечно малой частицы в пределе получим, что
представляет собой кинетическую энергию частицы, поэтому для бесконечно малой частицы в пределе получим, что 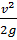 есть кинетическая энергия в точке потока жидкости, рассчитанная не единицу веса.
есть кинетическая энергия в точке потока жидкости, рассчитанная не единицу веса.
Сумма потенциальной и кинетической энергии называется механической энергией. Обозначая через 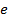 механическую энергию в точке потока, рассчитанную на единицу веса, в соответствии со сказанным, получим
механическую энергию в точке потока, рассчитанную на единицу веса, в соответствии со сказанным, получим
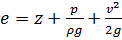 .
.
Следовательно, уравнение Бернулли для линии тока можно представить в виде:
 .
. 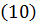
Это означает, что механическая энергия, рассчитанная на единицу веса, во всех точках одной и той же линии тока одинакова. Поскольку при установившемся движении жидкости линии тока совпадают с траекториями движения частиц, то из уравнения 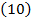 следует, что при таком движении механическая энергия любой частицы идеальной (или не вязкой) несжимаемой жидкости на всем пути ее меняется. Это, однако, не означает, что слагаемые механической энергии частицы не изменяются при ее перемещении. В общем случае движения соотношение слагаемых механической энергии частицы жидкости зависит от формы границ потока и задаваемых граничных условий.
следует, что при таком движении механическая энергия любой частицы идеальной (или не вязкой) несжимаемой жидкости на всем пути ее меняется. Это, однако, не означает, что слагаемые механической энергии частицы не изменяются при ее перемещении. В общем случае движения соотношение слагаемых механической энергии частицы жидкости зависит от формы границ потока и задаваемых граничных условий.
Механическая энергия в точках потока, рассчитанная на единицу веса протекающей жидкости называется удельной механической энергией и, следовательно, энергетический смысл уравнения Бернулли можно выразить в следующем виде: удельная механическая энергия во всех точках данной линии тока одинакова при установившемся вихревом движении невязкой несжимаемой жидкости.
2.4. Уравнение Бернулли для установившегося течения вязкой несжимаемой жидкости записывается в следующем виде:
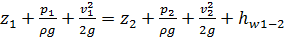 ,
, 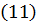
где 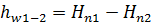
В этом уравнении все члены, за исключением  , имеют геометрическое представление, а так же гидродинамический и энергетический смысл такие же, как и члены уравнения Бернулли для невязкой несжимаемой жидкости. Поэтому, используя те же обозначения для гидродинамического напора и удельной механической энергии, рассчитанной на единицу веса, уравнение Бернулли
, имеют геометрическое представление, а так же гидродинамический и энергетический смысл такие же, как и члены уравнения Бернулли для невязкой несжимаемой жидкости. Поэтому, используя те же обозначения для гидродинамического напора и удельной механической энергии, рассчитанной на единицу веса, уравнение Бернулли 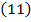 можно представить еще в следующих двух видах:
можно представить еще в следующих двух видах:
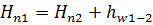 ,
, 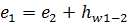
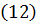
Из уравнения  видим, что
видим, что  имеет размерность длины, т.е. такую же, как и все его другие члены. Поэтому ее можно изобразить вертикальными отрезками, как показано на рисунке (в уравнениях Бернулли ось
имеет размерность длины, т.е. такую же, как и все его другие члены. Поэтому ее можно изобразить вертикальными отрезками, как показано на рисунке (в уравнениях Бернулли ось 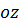 направлена против силы тяжести).
направлена против силы тяжести).
Из уравнения  следует, что при установившемся движении
следует, что при установившемся движении  представляет собой разность между гидродинамическими напорами в точках 1 и 2, взятых на одной и той же линии тока, причем всегда
представляет собой разность между гидродинамическими напорами в точках 1 и 2, взятых на одной и той же линии тока, причем всегда 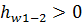 , так как всегда
, так как всегда 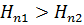 и, следовательно, гидродинамический напор в точке 2 всегда меньше гидродинамического напора в точке 1.
и, следовательно, гидродинамический напор в точке 2 всегда меньше гидродинамического напора в точке 1.
В связи с этим  называют потерей гидродинамического напора на участке тока 1-2. Очевидно, что в таком случае напорная линия
называют потерей гидродинамического напора на участке тока 1-2. Очевидно, что в таком случае напорная линия 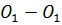 вдоль линии тока всегда будет понижающейся линией (рисунок 5). Ее уклон обозначают обычно через
вдоль линии тока всегда будет понижающейся линией (рисунок 5). Ее уклон обозначают обычно через 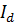 или
или 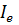 и определяют по следующей формуле:
и определяют по следующей формуле:
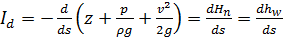 .
.
Изменения статического напора  и пьезометрического напора
и пьезометрического напора 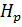 и здесь избираются так же, как это было показано при анализе уравнения Бернулли для невязкой жидкости.
и здесь избираются так же, как это было показано при анализе уравнения Бернулли для невязкой жидкости.
Выясним энергетический смысл члена  . Из уравнения
. Из уравнения 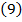 следует, что
следует, что  определяет разность между значениями удельных механических
определяет разность между значениями удельных механических
энергий в точках 1 и 2, взятых на одной и той же линии тока. Эта разность удельных механических энергий затрачивается на работу сил вязкости при перемещении единицы веса жидкости по линии тока на участке ее от точки 1 до точки 2. Поэтому член  еще называется потерей удельной механической энергии на линии тока. При установившемся движении вязкой несжимаемой жидкости удельная механическая энергия по линии тока в направлении течения жидкости непрерывно уменьшается. Закон сохранения энергии при этом не нарушается, ибо потерянная механическая энергия, затраченная на работу сил вязкости, превращается в тепловую энергию (рисунок 5).
еще называется потерей удельной механической энергии на линии тока. При установившемся движении вязкой несжимаемой жидкости удельная механическая энергия по линии тока в направлении течения жидкости непрерывно уменьшается. Закон сохранения энергии при этом не нарушается, ибо потерянная механическая энергия, затраченная на работу сил вязкости, превращается в тепловую энергию (рисунок 5).

Рисунок 5 – Интерпретация слагаемых уравнения Бернулли для вязкой несжимаемой жидкости.
При установившимся движении уравнение Бернулли можно записать в следующем виде (для двух точек одной линии тока):
 ,
,
при чем
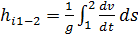 .
.
Все члены в этом уравнении за исключением 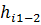 , имеют тот же смысл, что и члены уравнения Бернулли, поэтому его можно записать еще в следующих двух формах:
, имеют тот же смысл, что и члены уравнения Бернулли, поэтому его можно записать еще в следующих двух формах:
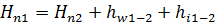 ,
, 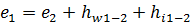
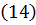
Из уравнения 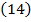 следует, что член
следует, что член 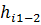 определяет локальное изменение во времени кинетической энергии жидкости, рассчитанной на единицу веса ее на участке линии тока между точками 1 и 2. Такое изменение кинетической энергии обусловлено локальными силами инерции. Величина
определяет локальное изменение во времени кинетической энергии жидкости, рассчитанной на единицу веса ее на участке линии тока между точками 1 и 2. Такое изменение кинетической энергии обусловлено локальными силами инерции. Величина 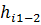 имеет линейную размерность и называется инерционным напором.
имеет линейную размерность и называется инерционным напором.
В отличии от всех других членов уравнения Бернулли инерционный напор может быть положительным и отрицательным в зависимости от знака производной  . Если на всей длине линии тока (между точками 1 и 2)
. Если на всей длине линии тока (между точками 1 и 2) 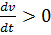 , то инерционный напор будет положительным, и тогда
, то инерционный напор будет положительным, и тогда 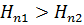 как это показано на рисунке 5.
как это показано на рисунке 5.
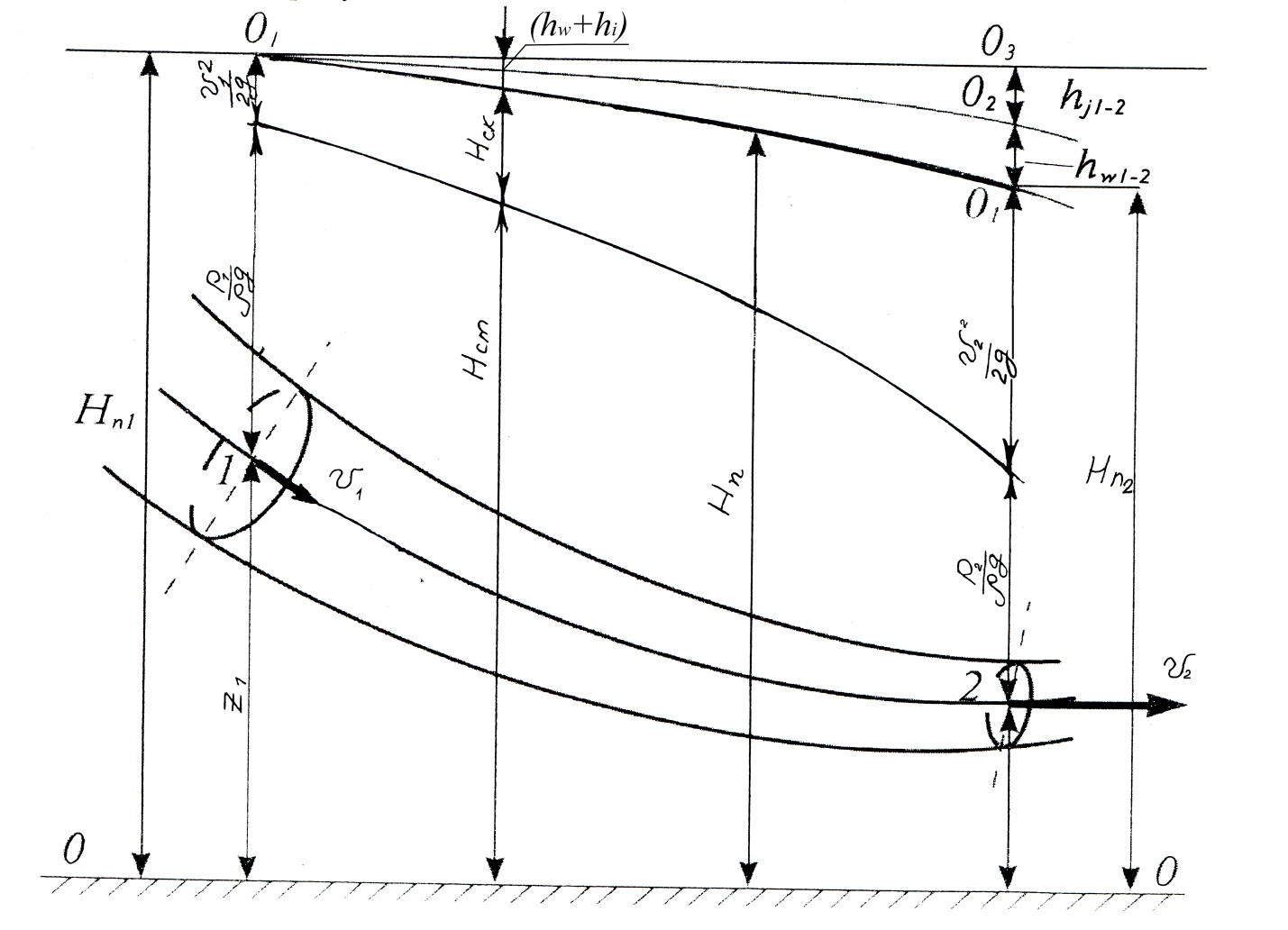
Рисунок 6 – Интерпретация слагаемых уравнения Бернулли для вязкой несжимаемой жидкости при неустановившемся движении в случае
Если же на том же участке линии тока везде 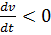 , то инерционный напор будет отрицательным. И тогда возможно, что гидродинамический напор в точке 2 будет больше, чем в точке 1, т.е.
, то инерционный напор будет отрицательным. И тогда возможно, что гидродинамический напор в точке 2 будет больше, чем в точке 1, т.е. 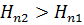 . В этом случае, несмотря на то, что течение происходит в прежнем направлении, удельная механическая энергия в точке 2 на линии тока может быть больше, чем в точке 1, и напорная линия
. В этом случае, несмотря на то, что течение происходит в прежнем направлении, удельная механическая энергия в точке 2 на линии тока может быть больше, чем в точке 1, и напорная линия 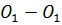 тогдабыла бы не падающей, как на рисунке 5, а восходящей. Если во всех точках на линии тока
тогдабыла бы не падающей, как на рисунке 5, а восходящей. Если во всех точках на линии тока  , то
, то  , как при установившемся движении невязкой жидкости.
, как при установившемся движении невязкой жидкости.
При неустановившемся движении изображения, подобные приведенным на рисунке 6, могут соответствовать лишь некоторому моменту времени, ибо в этом случае с течением времени форма всех линий изменяется.
Список литературы
1. Патрашев А.Н. Прикладная гидромеханика: А.Н. Патрашев, Л.А. Кивако, С.И. Гожий / М.:Воениздат, 1970 - 688с.
2. Чугаев Р.Р. Гидравлика: Учебник для вузов. – 4изд. – Л.:Энергоиздат. Ленингр. Отд-е, 1982 – 672с.
Министерство образования и науки Российской федерации
ФГБОУ ВПО «Алтайский государственный технический
университет им. И.И. Ползунова

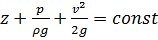 ,
,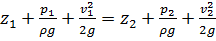
 – высотная отметка, или нивелирная высота, представляет собой расстояние по вертикали от рассматриваемой точки до некоторой плоскости
– высотная отметка, или нивелирная высота, представляет собой расстояние по вертикали от рассматриваемой точки до некоторой плоскости  (рисунок 2), которую называют плоскостью сравнения; второй -
(рисунок 2), которую называют плоскостью сравнения; второй -  называют высотой гидродинамического давления, а третий -
называют высотой гидродинамического давления, а третий - 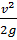 – скоростной высотой. Так как по уравнению Бернулли сумма этих трех членов вдоль линии тока неизменна, то вершины их суммарных отрезков, построенных в точках рассматриваемой линии тока, должны лежать в одной горизонтальной плоскости
– скоростной высотой. Так как по уравнению Бернулли сумма этих трех членов вдоль линии тока неизменна, то вершины их суммарных отрезков, построенных в точках рассматриваемой линии тока, должны лежать в одной горизонтальной плоскости 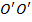 , параллельной плоскости
, параллельной плоскости 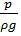 представляет высоту такого столба, который в данной точке линии тока создает давление, равное гидродинамическому давлению
представляет высоту такого столба, который в данной точке линии тока создает давление, равное гидродинамическому давлению  .
.
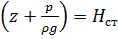 называют статическим напором (рисунок 2).
называют статическим напором (рисунок 2).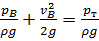 ,
,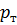 – давление в заторможенной жидкости у загнутого конца трубки. Если же из точки А трубку убрать, то по уравнению Бернулли получим
– давление в заторможенной жидкости у загнутого конца трубки. Если же из точки А трубку убрать, то по уравнению Бернулли получим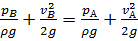 .
.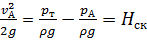

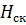 называют скоростным напором. Трубки с загнутым нижним концом, предназначенные для измерения скоростного напора, называют скоростными трубками или трубками Пито.
называют скоростным напором. Трубки с загнутым нижним концом, предназначенные для измерения скоростного напора, называют скоростными трубками или трубками Пито.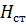 и скоростного напора
и скоростного напора 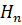
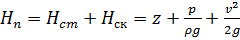
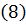
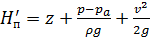 .
.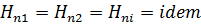 или
или 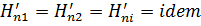
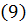
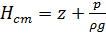 или пьезометрического напора
или пьезометрического напора 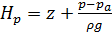 ,
,
 или пьезометрического уклона
или пьезометрического уклона  , которые определяются следующим образом:
, которые определяются следующим образом: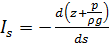 ,
, 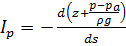 ,
, – элемент длины линии тока.
– элемент длины линии тока.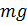 – вес частицы жидкости, то произведение
– вес частицы жидкости, то произведение  будет определять потенциальную энергию этой частицы относительно выбранной плоскости сравнения. Поделив
будет определять потенциальную энергию этой частицы относительно выбранной плоскости сравнения. Поделив 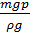 определяет потенциальную энергию давления, испытываемого частицей от окружающей жидкости, так как
определяет потенциальную энергию давления, испытываемого частицей от окружающей жидкости, так как 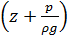 ,
,  представляет собой кинетическую энергию частицы, поэтому для бесконечно малой частицы в пределе получим, что
представляет собой кинетическую энергию частицы, поэтому для бесконечно малой частицы в пределе получим, что 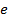 механическую энергию в точке потока, рассчитанную на единицу веса, в соответствии со сказанным, получим
механическую энергию в точке потока, рассчитанную на единицу веса, в соответствии со сказанным, получим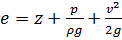 .
. .
. 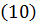
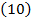 следует, что при таком движении механическая энергия любой частицы идеальной (или не вязкой) несжимаемой жидкости на всем пути ее меняется. Это, однако, не означает, что слагаемые механической энергии частицы не изменяются при ее перемещении. В общем случае движения соотношение слагаемых механической энергии частицы жидкости зависит от формы границ потока и задаваемых граничных условий.
следует, что при таком движении механическая энергия любой частицы идеальной (или не вязкой) несжимаемой жидкости на всем пути ее меняется. Это, однако, не означает, что слагаемые механической энергии частицы не изменяются при ее перемещении. В общем случае движения соотношение слагаемых механической энергии частицы жидкости зависит от формы границ потока и задаваемых граничных условий.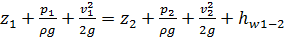 ,
, 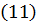
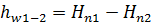
 , имеют геометрическое представление, а так же гидродинамический и энергетический смысл такие же, как и члены уравнения Бернулли для невязкой несжимаемой жидкости. Поэтому, используя те же обозначения для гидродинамического напора и удельной механической энергии, рассчитанной на единицу веса, уравнение Бернулли
, имеют геометрическое представление, а так же гидродинамический и энергетический смысл такие же, как и члены уравнения Бернулли для невязкой несжимаемой жидкости. Поэтому, используя те же обозначения для гидродинамического напора и удельной механической энергии, рассчитанной на единицу веса, уравнение Бернулли 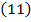 можно представить еще в следующих двух видах:
можно представить еще в следующих двух видах: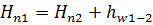 ,
, 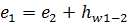
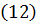
 видим, что
видим, что 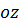 направлена против силы тяжести).
направлена против силы тяжести).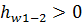 , так как всегда
, так как всегда 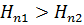 и, следовательно, гидродинамический напор в точке 2 всегда меньше гидродинамического напора в точке 1.
и, следовательно, гидродинамический напор в точке 2 всегда меньше гидродинамического напора в точке 1.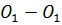 вдоль линии тока всегда будет понижающейся линией (рисунок 5). Ее уклон обозначают обычно через
вдоль линии тока всегда будет понижающейся линией (рисунок 5). Ее уклон обозначают обычно через 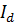 или
или 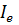 и определяют по следующей формуле:
и определяют по следующей формуле: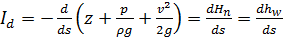 .
. и пьезометрического напора
и пьезометрического напора 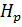 и здесь избираются так же, как это было показано при анализе уравнения Бернулли для невязкой жидкости.
и здесь избираются так же, как это было показано при анализе уравнения Бернулли для невязкой жидкости.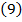 следует, что
следует, что 
 ,
,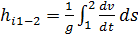 .
.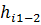 , имеют тот же смысл, что и члены уравнения Бернулли, поэтому его можно записать еще в следующих двух формах:
, имеют тот же смысл, что и члены уравнения Бернулли, поэтому его можно записать еще в следующих двух формах: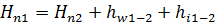 ,
, 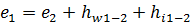
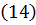
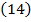 следует, что член
следует, что член  . Если на всей длине линии тока (между точками 1 и 2)
. Если на всей длине линии тока (между точками 1 и 2) 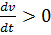 , то инерционный напор будет положительным, и тогда
, то инерционный напор будет положительным, и тогда 
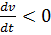 , то инерционный напор будет отрицательным. И тогда возможно, что гидродинамический напор в точке 2 будет больше, чем в точке 1, т.е.
, то инерционный напор будет отрицательным. И тогда возможно, что гидродинамический напор в точке 2 будет больше, чем в точке 1, т.е. 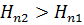 . В этом случае, несмотря на то, что течение происходит в прежнем направлении, удельная механическая энергия в точке 2 на линии тока может быть больше, чем в точке 1, и напорная линия
. В этом случае, несмотря на то, что течение происходит в прежнем направлении, удельная механическая энергия в точке 2 на линии тока может быть больше, чем в точке 1, и напорная линия  , то
, то  , как при установившемся движении невязкой жидкости.
, как при установившемся движении невязкой жидкости.


