Фазовые проницаемости
Фазовые проницаемости являются одной из важнейших характеристик процесса течения пластовых флюидов в породах-коллекторах нефти и газа. Функции относительных фазовых проницаемостей (ОФП) в зависимости от насыщенности используются при решении большого числа геологопромысловых задач. Данные о фазовых проницаемостях необходимы при обосновании кондиционных пределов петрофизических свойств пород, при промышленной оценке переходных нефтегазовых зон пластов, в газогидродинамических расчетах технологических показателей разработки, при выборе методов воздействия на пласт с целью увеличения нефтеотдачи, при анализе и контроле за разработкой залежей. Особое внимание уделено экспериментальным методам определения ОФП на образцах керна, которые считаются базовыми среди остальных методов. Экспериментальное определение зависимостей ОФП от водонасыщенности – трудоемкий процесс, требующий использования специальной аппаратуры, поэтому на практике часто применяют е методы получения ОФП по более доступным данным (промысловым или расчетным). Определение ОФП по данным геофизических исследований скважин методы расчета ОФП с использованием промысловых данных получили небольшое распространение Это вызвано неопределенностью в оценке распределения насыщенности в пласте величин перепадов давления и дренируемых объемов и др.
Расчет относительных фазовых проницаемостей по кривым капиллярное давление-насыщенность Для воспроизведения процессов совместного течения жидкостей в коллекторах с межзерновой пористостью широкое распространение получили капиллярные модели, в которых поровое пространство моделируется совокупностью капиллярных каналов. В зависимости от свойств моделируемой пористой среды и с целью более точного отражения их разработаны капиллярные модели различной степени сложности Рассмотрим использование простой капиллярной модели для расчета ОФП по кривой капиллярного давления. Кривая капиллярного давления может быть получена способами ртутной порометрии, центрифугирования, полупроницаемой мембраны, контактной эталонной порометрии и др. Уравнение, предложенное У.Пурселлом (1949 г.), устанавливает связь между проницаемостью К, пористостью m и кривой капиллярного давления Рк = f (S)
где λ – так называемый литологический множитель, учитывающий различие форм капилляров и реальных поровых каналов.
Для расчета ОФП по данной капиллярной модели предполагается, что смачивающая фаза с ростом насыщенности последовательно заполняет поры от меньших к большим. Тогда формулы для расчета ОФП, дающие наиболее близкие к экспериментальным значения, имеют вид (Burdine N., 1953):
. Расчет кривых относительной проницаемости для смачивающей и не смачивающей фаз (система нефть - вода или газ - вода) можно произвести по уравнениям, предложенным Бурдайном:
(2) где Кпротн с.ф., Кпротн н.с.ф. – относительные проницаемости смачивающей и несмачивающей фаз (воды и нефти), τ0сф, τ0нсф – коэффициент извилистости смачивающей и несмачивающей фаз, Кв – насыщенность смачивающей фазы, Рк – капиллярное давление, К - насыщенность. Бурдайн Н. Т. показал, что коэффициент извилистости можно рассчитать по формулам:
где Кв min – минимальная насыщенность смачивающей фазы, Кр нсф – равновесная насыщенность, при которой несмачивающая фаза становится подвижной (остаточная нефтенасыщенность). С учетом уравнения (3, 4), общие уравнения (1,2) для расчета кривых относительной проницаемости можно представить как:
где Кв св – остаточная водонасыщенность, Кно – остаточная нефтенасыщенность. Из уравнения (5, 6) вытекает, что кривые относительной проницаемости можно рассчитать по кривым капиллярного давления. Если кривые капиллярного давления представляются в виде
Рассмотрим построение кривых относительной проницаемости на конкретном примере. В результате исследований фильтрационных свойств образцов керна в лаборатории получили следующие данные:
По результатам исследований строится график кривых капиллярного давления, представленного в виде функции
Рис.1.7
Поверхность под графиком функции
Определяем относительную проницаемость воды:
Для S’ – площадь, рассчитанная от начала вытеснения до текущего интервала Кв
Остаточная водонасыщенность равна значению, в котором текущая водонасыщенность не изменяется с дальнейшим увеличением давления (график переходит в прямую, перпендикулярную оси абсцисс). Квсв – 11,3 % Кв = 90,0%, следовательно S’1 = 0,0250 ед., тогда∑∆S = 3,8345– 0, 0250 = 3,8095 ед2. Подставляя все данные в формулу получим (текущую и остаточную водонасыщенность подставляем в долях от единицы):
Кв = 80,99%, S’2 = 0, 0926 ед2, ∑∆S = 3,8345 – 0, 0926 = 3,7419 ед2.
Кв = 70,8%, S’3 = 0, 2200 ед2, Кв = 50,2%, S’4 = 0, 6320 ед2, Кв = 26,4%, S’5 = 1,5245 ед2, Кв = 17,4%, S’6 = 2, 1995 ед2, Кв = 13,5%, S’7 = 2,7845 ед2, Кв = 12,0%, S’8 = 3,3095 ед2, Кв = 11,3%, S’9 = 3,8345 ед2,
Рассчитываем относительную проницаемость нефти: Для Кно = 10% - коэффициент остаточной нефтенасыщенности (в долях от единицы Кно= 0, 1).
Все остальные величины те же самые. Кв = 90,0 %, Квсв = 11,3%, Sобщ. = 3,8345 ед2., S1 =
Кв = 80,99%, S2 =
Кв = 70,8%, S3 = Кв = 50,2%, S4 = Кв = 26,4%, S5 = Кв = 17,4%, S6 = Кв = 13,5%, S7 = Кв = 12,0%, S8 = Кв = 11,3%, S3 =
По полученным данным
Наиболее достоверными считаются прямые определения ОФП на керне изучаемого пласта-коллектора, в лабораторных условиях при стационарной или нестационарной фильтрации, в условиях моделирующих пластовые. Базовым является метод стационарной фильтрации, на который разработан отраслевой стандарт: ОСТ 39-235-89 «Нефть. Метод определения фазовых проницаемостей в лабораторных условиях при совместной стационарной фильтрации»
|

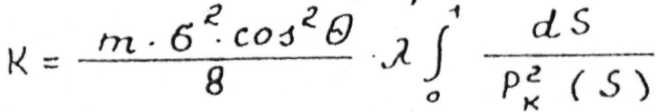 , (8)
, (8)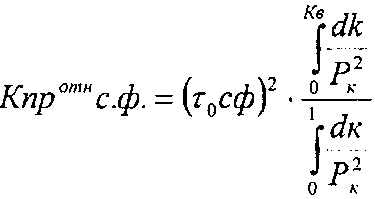 (1)
(1)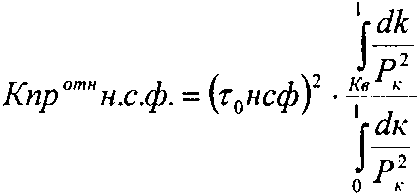
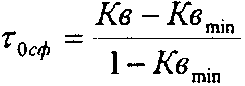 (3)
(3)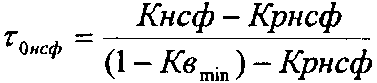 (4)
(4)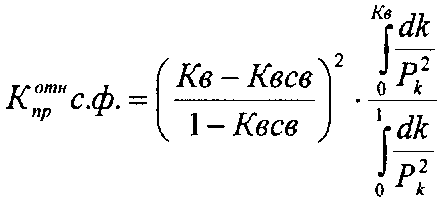 (5)
(5)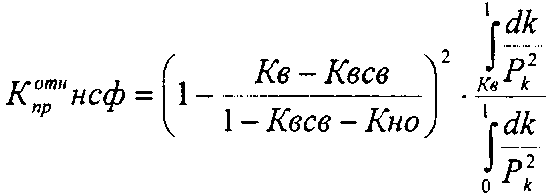 (6)
(6)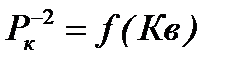 ,то вычисление интегралов сводится к суммированию отношений элементарных площадей. В упрощенном виде уравнения (5, 6) имеют вид:
,то вычисление интегралов сводится к суммированию отношений элементарных площадей. В упрощенном виде уравнения (5, 6) имеют вид: (7)
(7) (8)
(8) . Рис.1.7
. Рис.1.7

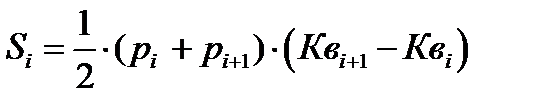
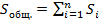

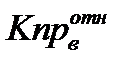 величина ∑∆S будет равна (Sобщ. – S’), где:
величина ∑∆S будет равна (Sобщ. – S’), где:

 =0,4242
=0,4242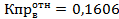
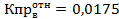

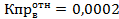
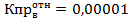
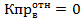 ,0000
,0000



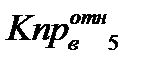
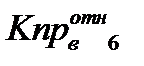
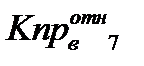


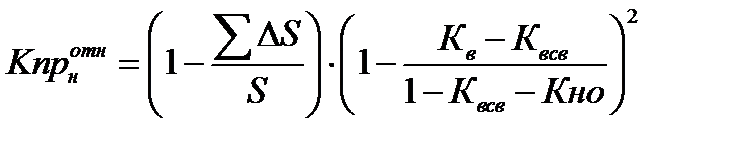
 величина ∑∆S будет равна S1, S2, … Sn.
величина ∑∆S будет равна S1, S2, … Sn. ед2
ед2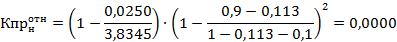
 ед2
ед2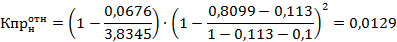
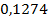 ед2,
ед2, 
 ед2,
ед2, 
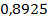 ед2,
ед2, 
 ед2,
ед2, 
 ед2,
ед2, 
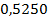 ед2,
ед2, 



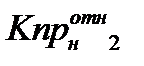





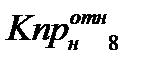
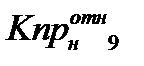
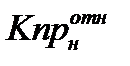 и
и 





