Макромоделювання автогенератора.
Практична і лабораторна робота 7 з дисципліни „Моделювання систем”. Макромоделювання автогенератора. Схема генератора на одному транзисторi, що є об’єктом моделювання, зображена на рис.1 вхідною мовою MicroCap-7.
Застосуємо модель Гамерштейна та метод оберненої лiнiйної пiдсистеми до побудови макромоделi генератора сигналу, близького до гармонiчного. Рівняння макромоделі мають вигляд
що вiдповiдає схемi на рис.2.
На рис.1 показана електрична схема макромоделі, що складається з двох інтеграторів з ідеальних джерел струму та одиничних ємностей, та нелінійного джерела напруги Е, коефіцієнти якого показані під схемою макромоделі. За вихiдним сигналом генератора (напруга вузла 5 на рис.1) визначено період встановлених коливань після завершення перехідного процесу Т =0.433е-6 сек. Відповідне значення квадрату частоти ω 2=2.106е14 є єдиним параметром лiнiйної консервативної пiдсистеми другого порядку з одиничною передачею в статиці:
Для обчислення внутрiшнього сигналу v як вихiдного оберненої пiдсистеми, послiдовним диференцiюванням (рис.1) з постійною часу τ =4е-9 сек. знайдено другу похiдну 300 відліків сигналів Цей файл передано MatLab-програмі ідентифікації нелінійної підсистеми, текст якої наведено нижче. %********** Synthesis generator macromodel ****************** clear; global Kd; load gener.usr; m=max(size(gener))/3; t=gener(1:2:m); y=gener(2:2:m); y1=gener(m+2:2:m*2); v=gener(m*2+2:2:m*3); %**** Macromodel construction ******************************* m=max(size(t)); format short e; B=v; % Matrics of equation A*K=B A=[ones(size(y)) y y1 y.^2 y.*y1 y1.^2 y.^3 y.^2.*y1 y.*y1.^2... y1.^3 y.^4 y.^3.*y1 y.^2.*y1.^2 y.*y1.^3 y1.^4... y.^5 y.^4.*y1 y.^3.*y1.^2 y.^2.*y1.^3 y.*y1.^4 y1.^5 ]; kk=max(abs(A)); % Normalization for i=1:size(A,2); A(:,i)=A(:,i)/kk(i); end; p=20; A=A(p+1:m,:); B=B(p+1:m); % Elimin. of primers p points red=ones(size(A)); redc=zeros(size(kk')); rc=1; u=0; kkm=max(size(kk)); %**** Cycle of a reduction (rc - counter of iterations) ************** % On each iterat. the coef. with max relat. deviation is deleted while (u<kkm-u-rc+2); A=A.*red; %**** Tihonov’s regularization ******************************** alfa=5e-2; % The factor of regularization (>=0) AR=[A; alfa*diag(ones(size(kk)))]; % Matrix with regularization BR=[B; zeros(size(kk'))]; %**** Approximating by the least squares method ***************** K=AR\BR; MeanQuadEr=sum((A*K-B).^2)/m; % Mean squares deviation Kd=[K./kk']; % Denormalization %*** Metod of reduction (delta is the factor of stoh. permut. А & В) *** delta=1e-10; rB=delta*abs(B).*randn(size(B)); rA=delta*abs(A).*randn(size(A)); Kr=[A+rA;alfa*diag(ones(size(kk)))]\[B+rB;zeros(size(kk'))]; er=abs((K-Kr)./(K+delta)); [ermax,i]=max(er); % max rel. deviation red(:,i)=0; redc(rc)=i; rc=rc+1; er=sort(er); [ermin,j]=min(er(rc-1:kkm)); % min rel. deviation>0 limit=(ermax-ermin)/2; u=0; for j=1:kkm; if (er(j)>limit); u=u+1; end;end; end; redc, rc=rc-1 % End of cycle of reduction %**** Integrating of differential equations of model **************** tlimit=[0, 2e-6]; y0=[0.6, 2.5e6]; [tm,ym]=ode15s(@gener_pow,tlimit,y0); plot(t,y,'b',tm,ym(:,1),'r'); title('Output signal of generator and macromodel'); %pause;
Програма здійснює апроксимацію нелінійної функції двох аргументів степеневим поліномом із застосуванням комбінованої регуляризації – за Тіхоновим та редукцією полінома. Крім того, рівняння макромоделі розв’язуються для остаточної оцінки якості макромоделі. Вся програма розділена на функціональні блоки. Коротко розглянемо роботу кожного блоку. Спочатку програма формує масиви сигналу генератора y, його похідної y1 та внутрішнього сигналу макромоделі v, використовуючи масив gener.usr. Далі розв’язується регуляризована задача
із застосуванням редукції двовимірного степеневого поліному. Для цього спочатку формуються матриці А та В лінійної алгебраїчної системи А·К=В для степеневого поліному п’ятого степеня від двох змінних – y та y1. Кожне з рівнянь алгебраїчної системи є рівнянням нелінійної підсистеми з (1):
де індекс m позначає відповідну змінну в момент часу tm. Застосовано нормування матриці А за найбільшими елементами кожного стовпця. Вектор нормування kk використовується при денормуванні обчисленого вектора коефіцієнтів апроксимації К. Перші р часових точок перехідного процесу, які містять найбільші похибки, видаляються з алгебраїчної системи. Далі починається цикл комбінованої редукції апроксимуючого поліному. Масив red містить нульові стовпці, що відповідають видаленим членам полінома, а в масиві redc накопичуються порядкові номери видалених членів. Регуляризація за Тіхоновим полягає в доповненні системи М рівнянь (4) додатковими рівняннями α·kij =0; i, j =0,…,5; i + j ≤5; що еквівалентно задачі (3). Сформована система розв’язується за методом найменших квадратів з можливим виводом результатів на екран та підрахунком середньоквадратичної похибки апроксимації. Завершується цикл редукції видаленням члена поліному з найбільшим відносним відхиленням внаслідок випадкових збурень алгебраїчної системи. В цілому внаслідок редукції отримуємо набір коефіцієнтів двовимірного поліному з певною кількістю нульових коефіцієнтів. Процедура редукції зменшує кількість ненульових коефіцієнтів апроксимації нелінійної функції з 20 до 5. Для М=300 та α=0.05 відповідний редукований поліном має вигляд: V(12)=0.45437+0.43143·V(11)4-1.9343e-13·V(11)3·V(10)2+1.0573e-19·V(11)2·V(10)3-5.4322e-33·V(10)5. Останній блок програми здійснює інтегрування повних рівнянь макромоделі, записаних у MATLAB-функції gener_pow.m., та візуальне порівняння вихідних сигналів макромоделі і генератора.
function dydt=gener_pow(t,y); global Kd; F=Kd(1)+Kd(2)*y(1)+Kd(3)*y(2)... +Kd(4)*y(1)^2+Kd(5)*y(1)*y(2)+Kd(6)*y(2)^2... +Kd(7)*y(1)^3+Kd(8)*y(1)^2*y(2)+Kd(9)*y(1)*y(2)^2+Kd(10)*y(2)^3... +Kd(11)*y(1)^4+Kd(12)*y(1)^3*y(2)+Kd(13)*y(1)^2*y(2)^2... +Kd(14)*y(1)*y(2)^3+Kd(15)*y(2)^4... +Kd(16)*y(1)^5+Kd(17)*y(1)^4*y(2)+Kd(18)*y(1)^3*y(2)^2... +Kd(19)*y(1)^2*y(2)^3+Kd(20)*y(1)*y(2)^4+Kd(21)*y(2)^5; dydt=[ y(2); 2.306e14*(F-y(1)) ];
На рис.3 показано перехiдний процес у генераторi та в макромоделi згiдно iз описом на рис.1. Спочатку показані проекція фазового портрету генератора на площину (V(4), V(4)`), i фазовий портрет макромоделі. Нижче – часові залежності вихідних напруг.
Встановлений режим відтворюється з максимальною відносною похибкою 6%. Помітну похибку відтворення перехідного процесу можна пояснити неможливістю адекватного перерахунку початкових умов генератора та макромоделі. Адже схема генератора шостого порядку, тоді як макромодель – лише другого.
Хід лабораторної роботи. 1. Вивчити схеми автогенератора та його макромоделі. 2. Отримати в МС-7 числові масиви для ідентифікації нелінійної функції в MATLAB-6. 3. Набрати та відлагодити програму ідентифікації нелінійної функції в MATLAB-6. 4. Отримати фазові портрети та графіки перехідних процесів у автогенераторі та макромоделі. 5. Написати та захистити звіт.
|
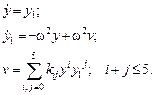, (1)
. (2)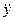
. Тоді внутрішній сигнал макромоделі v обчислюється за рівнянням (2). На рис.1 сигнал v є напругою вузла 9.
та 
, яким відповідають напруги вузлів 4, 7 і 9 на рис.1, записано у файл результатів аналізу gener.usr програми MicroCap-7.
(3)
; (4)
