
- Основные правила нахождения производной
1. 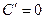 2.
2. 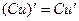 3.
3. 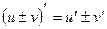 4.
4. 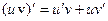
5. 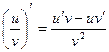 6.
6. 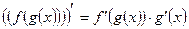
- Таблица производных основных функций
1.  2.
2.  3.
3.  4.
4. 
5. 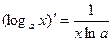 6.
6.  7.
7. 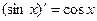 8.
8. 
9.  10.
10.  11.
11. 
12. 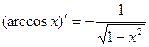 13.
13. 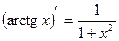 14.
14. 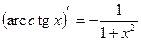 .
.
- Найти производные функций
а)  ; б)
; б) 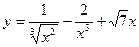 ; в)
; в) 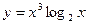 ; г)
; г) 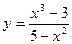 .
.
- Найти производные функций
а) 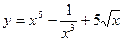 ; б)
; б)  ; в)
; в)  ; г)
; г) 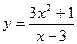 .
.
- Найти производные функций
а) 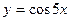 ; б)
; б)  ; в)
; в) 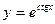 ; г)
; г) 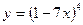 ; д)
; д) 
е)  ; ж)
; ж)  ; з)
; з) 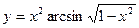 ; и)
; и) 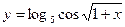 .
.
- Найти производные функций
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 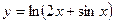
е) 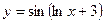 ; ж)
; ж) 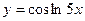 ; з)
; з)  ; и)
; и) 
к) 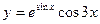 ; л)
; л)  ; м)
; м) 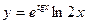 ; н)
; н) 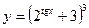

3. Геометрический смысл производной:
Число  - это угловой коэффициент касательной к графику функции
- это угловой коэффициент касательной к графику функции 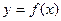 в точке с абсциссой
в точке с абсциссой  .
.
4. Уравнение касательной к графику функции 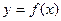 в точке
в точке 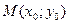 :
:

- Составить уравнение касательной к графику функции
 в точке с абсциссой
в точке с абсциссой 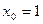 .
. - Составить уравнение касательной к графику функции
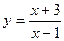 параллельно прямой
параллельно прямой 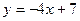 .
. - Составить уравнение касательной к графику функции
 , проходящей через точку
, проходящей через точку  .
. - Составить уравнение общей касательной к графикам функций

 и
и  .
. - Найти производные n -го порядка: а)
 ; б)
; б) 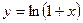 ; в)
; в)  .
.
 5. Правило Лопиталя:
5. Правило Лопиталя:
 .
.
1. Используя правило Лопиталя, найдите пределы
а) 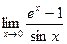 ; б)
; б)  ; в)
; в)  .
.

6. Схема отыскания наибольшего и наименьшего значения функции на отрезке:
1) Найти производную функции 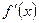 .
.
2) Найти критические точки функции (для этого решить уравнение  ). Отобрать из них только те, которые принадлежат указанному отрезку.
). Отобрать из них только те, которые принадлежат указанному отрезку.
3) Найти значение функции в критических точках, отобранных в предыдущем пункте, и на концах отрезка. Выбрать из них наименьшее и наибольшее.
7. Схема отыскания наибольшего и наименьшего значения функции на интервале:
1) Найти производную функции 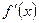 .
.
2) Найти критические точки функции (для этого решить уравнение  ).
).
3) Если на интервале функция имеет единственную точку экстремума и это точка максимума, то в ней функция принимает наибольшее значение. Если на интервале функция имеет единственную точку экстремума и это точка минимума, то в ней функция принимает наименьшее значение.
1. Найти наибольшее и наименьшее значения функции 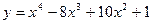 на отрезке
на отрезке
а)  ; б)
; б)  .
.
2. Окно имеет форму прямоугольника, завершенного полукругом. При заданном периметре Р окна найти такие его размеры, чтобы оно пропускало наибольшее количество света.
8. Формула Тейлора.
 1) Формула Тейлора:
1) Формула Тейлора:

2) Формула Маклорена (получается из формулы Тейлора при  ):
):
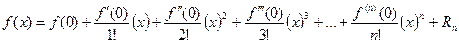
3) Разложение элементарных функций по формуле Маклорена:
 ;
;

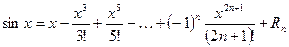 ;
;
 ;
;
 ;
;
 ;
;
 .
.
- Функцию
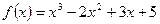 разложить по степеням
разложить по степеням  по формуле Тейлора.
по формуле Тейлора. - Функцию
 разложить по степеням
разложить по степеням  до члена, содержащего
до члена, содержащего 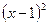 .
. - Функцию
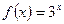 представить в виде многочлена третьей степени по х.
представить в виде многочлена третьей степени по х. - Используя разложение в ряд Маклорена, вычислить
 с точностью до 0,001.
с точностью до 0,001.
Домашнее задание
- Найти производные функций:
а)  ; б)
; б)  ; в)
; в) 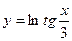 ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и) 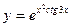 ; к)
; к) 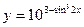 .
.
- Составить уравнение касательной к графику функции
 в точке пересечения с осью ординат.
в точке пересечения с осью ординат. - Составить уравнение касательной к графику функции
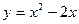 перпендикулярно прямой
перпендикулярно прямой 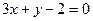 .
. - Найти производные n -го порядка: а)
 ; б)
; б) 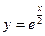 ; в)
; в)  .
. - Используя правило Лопиталя, найдите пределы:
а)  ; б)
; б)  ; в)
; в)  .
.
- Найти наибольшее и наименьшее значения функции
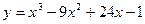 на отрезке
на отрезке
а)  ; б)
; б)  .
.
- Требуется выделить прямоугольную площадку земли в 512 м2, огородить ее забором и разделить загородкой на три равные части параллельно одной из сторон площадки. Каковы должны быть размеры площадки, чтобы на постройку заборов пошло наименьшее количество материала?
- Функцию
 разложить по степеням
разложить по степеням  по формуле Тейлора.
по формуле Тейлора. - Функцию
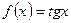 разложить по формуле Маклорена до члена
разложить по формуле Маклорена до члена  включительно.
включительно. - Используя разложение в ряд Маклорена, вычислить
 с точностью до 0,001.
с точностью до 0,001.
9. Дифференциал функции:
 1)
1) 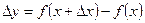 - приращение функции.
- приращение функции.
2)  или
или  - дифференциал функции.
- дифференциал функции.
3)  - применение дифференциала в приближенных вычислениях.
- применение дифференциала в приближенных вычислениях.
4)  - дифференциалы высших порядков.
- дифференциалы высших порядков.
1. Найти приращение и дифференциал функции:
а)  при
при 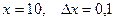 ; б)
; б)  при
при  .
.
2. Вычислить приближенно
а)  ; б)
; б) 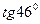 ; в)
; в)  .
.
3.  . Найти
. Найти 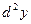 .
.
4. 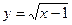 . Найти
. Найти 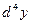 .
.


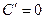 2.
2. 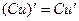 3.
3. 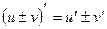 4.
4. 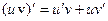
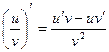 6.
6. 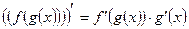
 2.
2.  3.
3.  4.
4. 
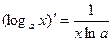 6.
6.  7.
7. 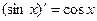 8.
8. 
 10.
10.  11.
11. 
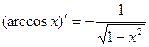 13.
13. 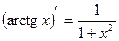 14.
14. 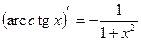 .
. ; б)
; б) 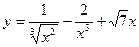 ; в)
; в) 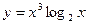 ; г)
; г) 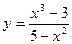 .
.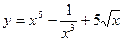 ; б)
; б)  ; в)
; в)  ; г)
; г) 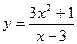 .
.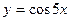 ; б)
; б)  ; в)
; в) 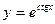 ; г)
; г) 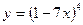 ; д)
; д) 
 ; ж)
; ж)  ; з)
; з) 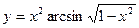 ; и)
; и) 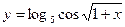 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 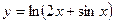
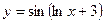 ; ж)
; ж) 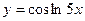 ; з)
; з)  ; и)
; и) 
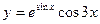 ; л)
; л)  ; м)
; м) 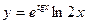 ; н)
; н) 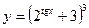

 - это угловой коэффициент касательной к графику функции
- это угловой коэффициент касательной к графику функции 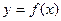 в точке с абсциссой
в точке с абсциссой  .
.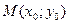 :
:
 в точке с абсциссой
в точке с абсциссой 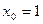 .
.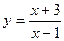 параллельно прямой
параллельно прямой 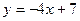 .
. , проходящей через точку
, проходящей через точку  .
.
 и
и  .
. ; б)
; б) 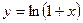 ; в)
; в)  .
. 5. Правило Лопиталя:
5. Правило Лопиталя: .
.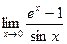 ; б)
; б)  ; в)
; в)  .
.
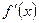 .
. ). Отобрать из них только те, которые принадлежат указанному отрезку.
). Отобрать из них только те, которые принадлежат указанному отрезку.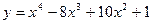 на отрезке
на отрезке ; б)
; б)  .
. 1) Формула Тейлора:
1) Формула Тейлора:
 ):
):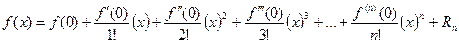
 ;
;
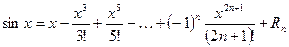 ;
; ;
; ;
; ;
; .
.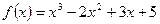 разложить по степеням
разложить по степеням  по формуле Тейлора.
по формуле Тейлора. разложить по степеням
разложить по степеням  до члена, содержащего
до члена, содержащего 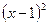 .
.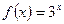 представить в виде многочлена третьей степени по х.
представить в виде многочлена третьей степени по х.  с точностью до 0,001.
с точностью до 0,001. ; б)
; б)  ; в)
; в) 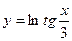 ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;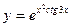 ; к)
; к) 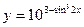 .
. в точке пересечения с осью ординат.
в точке пересечения с осью ординат.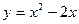 перпендикулярно прямой
перпендикулярно прямой 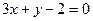 .
. ; б)
; б) 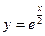 ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
.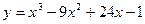 на отрезке
на отрезке  ; б)
; б)  .
. разложить по степеням
разложить по степеням  по формуле Тейлора.
по формуле Тейлора.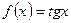 разложить по формуле Маклорена до члена
разложить по формуле Маклорена до члена  включительно.
включительно. с точностью до 0,001.
с точностью до 0,001. 1)
1) 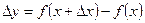 - приращение функции.
- приращение функции. или
или  - дифференциал функции.
- дифференциал функции. - применение дифференциала в приближенных вычислениях.
- применение дифференциала в приближенных вычислениях. - дифференциалы высших порядков.
- дифференциалы высших порядков. при
при 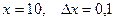 ; б)
; б)  при
при  .
. ; б)
; б) 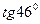 ; в)
; в)  .
. . Найти
. Найти 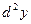 .
.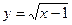 . Найти
. Найти 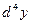 .
.



